오늘 정말 배울게 많다. 무엇인가를 해결하기 위해 알아보면 나뭇가지가 이어지듯 또다른 궁금증을 자아낸다. 하나하나 알아가는 재미가 쏠쏠하고 지식이 채워지는 느낌이 들면서도, 휘발성 메모리 마냥 배웠던 것이 날라가 버리지 않을까 걱정도 된다. 복습도 잘 해야겠다는 생각이 든다.
개요
우선 알고리즘을 알기 전에 가볍게 정의하자면
알고리즘이란 : 목적을 달성하기 위한 여러가지 행동들의 집합이다. 컴퓨터가 따라 할 수 있도록 문제를 해결하는 절차나 방법을 자세히 설명하는 과정이라고도 할 수 있겠다.
우리는 프로그램을 만들 때 프로그램이 크던 작던 데이터를 다루게 된다. 데이터의 구조는 이 데이터를 정리하는 것이다. 데이터를 어떻게 정리하는냐에 따라 문제를 해결하는 절차가 복잡하거나 간단해진다. 이는 우리가 프로그램을 실행할 때의 실행 속도에 영향을 준다. 즉, 우리가 어떤 데이터의 구조를 사용하느냐에 따라 우리의 서비스가 느려지거나 빨라지게 된다.
데이터의 구조에 따라 '정렬', '검색', '편집' 등에 최적화 되게 된다. 따라서 우리는 작업의 내용에 따라 무슨 데이터의 구조를 언제, 어떻게 잘 사용하는 것이 대단히 중요하다. 이것을 잘하기 위해서는 4가지의 오퍼레이션 상황에 맞춰서 데이터 구조에 대한 이해가 필요하다. (검색, 읽기, 삽입, 삭제) 이 4가지 상황을 염두에 두고 데이터를 보면 어떤 데이터 구조를 써야할지 알 수 있다.
알고리즘
알고리즘에는 시간 복잡도가 존재한다. 일을 처리하는데 얼마나 시간이 걸리느냐가 아닌 완료까지 얼마나 많은 절차/스텝이 필요한가를 따지는 수치이다. 같은 알고리즘이라도 하드웨어나 개인의 환경에 따라 처리속도가 달라지기 때문에 절차 수에 따라 비교하는 것이다. 당연히 적은 절차로 같은 작업을 수행하는 알고리즘이 더 훌륭한 알고리즘이다.
Big-O
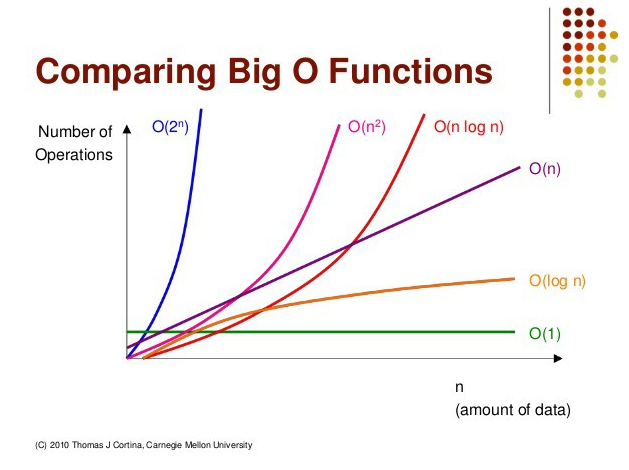
시간 복잡도의 경우를 간단하게 표현한 것이Big-O이다. 풀어서 설명하자만 입력한 사이즈에 따라 필요한 절차(스텝)의 양을 말하는 것이다. 예를 들어 아래의 선형 검색 알고리즘의 경우 입력한 수가 N개라면 필요한 절차도 N개 이므로 선형 검색의 시간 복잡도는 O(N) 이다. 이러한 개념을 우리는 Big-O라고 하고 이것을 활용해 시간복잡도를 빠르게 설명하는 것이 가능하다. 따라서 알고리즘 분석을 빠르게 할 수 있고 프로젝트를 할 때 적합한 알고리즘을 쉽게 접목시킬 수 있다.
이것에 대해 자세한 개념은 아래 유튜브 영상이 매우 잘 설명해준다.
노마드 코더 유튜브 (개발자라면 이제는 알아야하는 Big O 설명해드림. 10분컷) :
https://www.youtube.com/watch?v=BEVnxbxBqi8&list=PL7jH19IHhOLMdHvl3KBfFI70r9P0lkJwL&index=4
1. 검색 알고리즘 (Searching Argorithm)
검색 알고리즘은 데이터를 모아둔 곳에서 원하는 값을 가진 원소를 찾아내는 것이다. 검색알고리즘에는 두가지 접근방법이 있다.
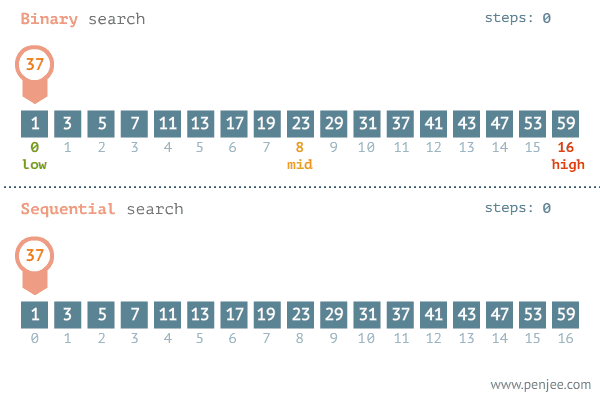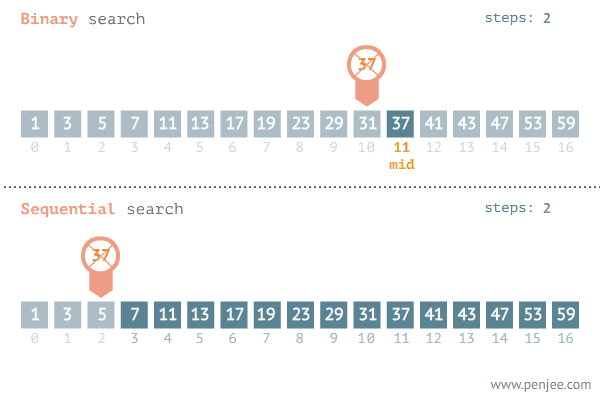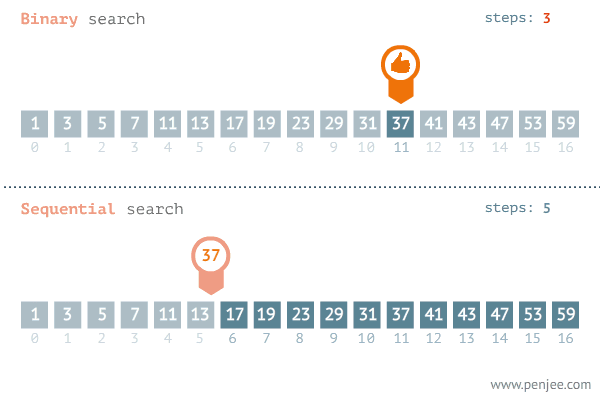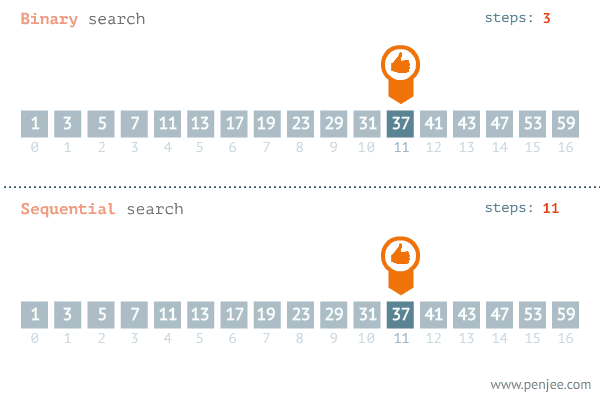
출처 : https://blog.penjee.com/binary-vs-linear-search-animated-gifs/
1 - 1. 선형 검색 (Linear Search)
어떻게 보면 매우 자연스러우면서도 단순한 알고리즘이다. 위의 그림처럼 만약 37이라는 숫자를 찾는다고 했을 때 왼쪽부터 차례로 37이 맞는지 확인을 하며 목표값을 찾는 것을 선형 검색 알고리즘이라고 한다.
이러한 선형검색의 최악의 경우는 우리가 찾는 목표값이 배열 맨 마지막에 있거나 아예 배열에 없는 경우이다. 극단적으로 생각해서 배열의 수가 1억개라고 가정 했을 때, 두 경우는 배열에 있는 1억개의 원소들을 모두 확인하는 과정을 거쳐야한다. 최악의 경우를 가정한다면 선형 검색을 하는 시간은 배열이 길어지면 길어질수록 똑같이 오래 걸릴 수 밖에 없다. 이것을 그래프로 나타내보면 다음과 같다.
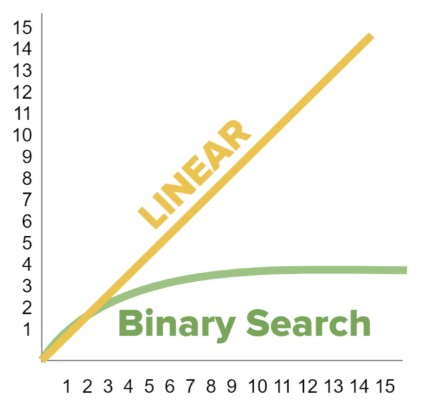
x축은 input(입력)의 수, y축은 time(시간)이다.
선형 검색 알고리즘의 경우 위의 그래프에서 Linear 직선 그래프처럼 입력한 수에 따라 정비례로 처리시간이 길어진다. 그래서 (Linear Searching Algorithm) 선형 검색 알고리즘이라고 부른다.
1 - 2. 이진 검색 (Binary Search)
선형 검색 알고리즘은 입력수가 많아짐에 따라 매우 비효율적이란것을 알 수 있다.
그렇다면 '이것보다 개선된 알고리즘은 없을까?' 그래서 나온 알고리즘이 바로 이진 검색 알고리즘이다. 위의 움짤에도 볼 수 있듯 이진 검색은 데이터배열을 반으로 쪼개서 조건을 확인한 후, 아닌쪽은 아예 검색 대상에서 제외 시켜버린다. 이후 남은 반은 다시 반으로 쪼개서 같은 과정을 거치며 검색을 실행한다. 이렇게 되면 아무리 검색 수가 많아지더라도 원하는 검색값을 순식간에 찾을 수 있다.
그렇다면 '선형 검색 알고리즘은 아예 안쓰고 이진 검색 알고리즘만 쓰면되지 않나?' 라고 생각할 수 있지만 안타깝게도 그렇지 않다. 조금만 생각해보면 알 수 있는데 이진 검색 알고리즘을 실행하기 위해선 반드시 배열이 정렬되어야만 한다. 선형 검색은 어느 데이터 배열에도 접근 가능하지만 이진 검색 알고리즘은 정렬 알고리즘을 통해 배열을 정렬한 뒤 실행이 가능하다. 따라서 간단하고 적은 배열의 수는 선형 검색 알고리즘이, 큰 배열의 경우는 이진 검색 알고리즘이 유리하다.
2. 정렬 알고리즘 (Sorting Argorithm)
Sorting 이란 정렬, 정리를 의미하는 말로 Sorting Argorithm 은큰 수에서 작은수, A-Z 기준 정렬 등 데이터를 어떠한 기준으로 정리하는 것을 뜻한다.
Big O는 알고리즘의 퍼포먼스를 효과적으로 보여준다 그러나 언제나 모든 알고리즘을 완벽하게 설명하지 못한다. 정렬 알고리즘에서 그러한게 잘 드러나는데 같은 Big O값을 가지고 있지만 각각의 퍼포먼스는 매우 다르다.
2 - 1 버블 정렬 (Bubble Sort)
버블 정렬은 사실 잘 사용되지는 않지만, 이해하기 매우 쉽다.
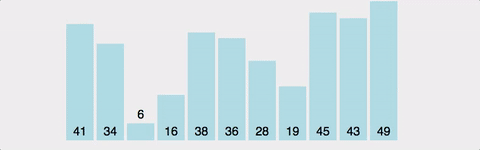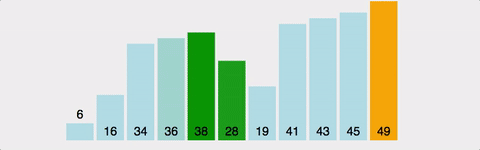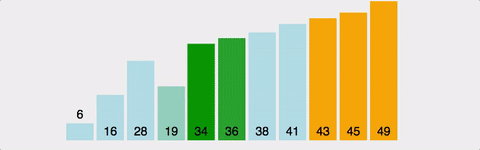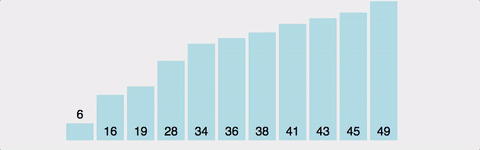
-
비유: 사람들의 키를 비교하며 두 명씩 바꾸는 것
- 옆에 있는 두 데이터를 비교하여 더 큰 값을 뒤로 보내는 과정을 반복한다.
- 마치 거품이 물 위로 떠오르듯 큰 값이 배열의 끝으로 이동합니다.
-
과정:
- 배열을 여러 번 순회하면서 인접한 두 값을 비교하고, 필요하면 위치를 바꾼다.
- 최댓값이 배열 끝으로 이동한 뒤, 나머지 요소들을 다시 비교한다.
-
시간복잡도 :
O(N^2) -
c++로 버블 정렬을 나타내면 다음과 같다.
#include <iostream>
using namespace std;
void bubbleSort(int arr[], int n) {
for (int i = 0; i < n - 1; ++i) {
for (int j = 0; j < n - i - 1; ++j) {
if (arr[j] > arr[j + 1]) {
// Swap
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
int main() {
int arr[] = {64, 34, 25, 12, 22, 11, 90};
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Before sorting: ";
for (int i = 0; i < n; ++i) cout << arr[i] << " ";
cout << endl;
bubbleSort(arr, n);
cout << "After sorting: ";
for (int i = 0; i < n; ++i) cout << arr[i] << " ";
cout << endl;
return 0;
}2 - 2 선택 정렬 (Selection Sort)
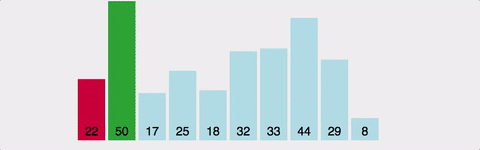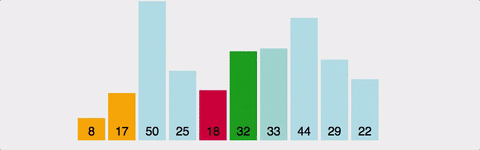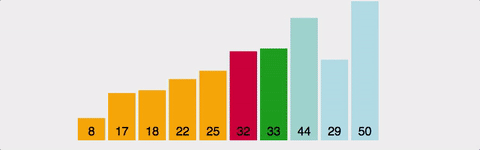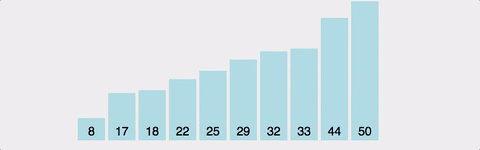
배열의 전체를 쭈욱 스캔하면서 가장 작은 값을 저장한 뒤 한쪽으로 쌓는느낌으로 진행되는 알고리즘이다. 아래그림을 보면 이해하기 쉽다. 버블 정렬과 유사하게 스왑도 있고, 비교도 있다. 그러나 매 사이클마다 여러번의 스왑을 해야할 수도 있는 버블정렬에 비해 선택정렬은 한번만 스왑하므로 선택정렬이 훨씬 낫다고 말할 수 있다. 그러나 시간복잡도는 마찬가지로 O(N^2) 이다.
-
비유: 카드 뭉치에서 가장 작은 카드를 하나씩 꺼내서 왼쪽에 정렬
- 배열에서 가장 작은 값을 찾아 배열의 맨 앞과 교환한다.
- 두 번째로 작은 값을 찾아 두 번째 위치에 교환하고, 이를 끝까지 반복한다.
-
과정:
- 남은 데이터 중 가장 작은 값을 선택한다.
- 선택된 값을 현재 위치와 바꿉니다
-
시간복잡도 :
O(N^2) -
c++로 선택 정렬을 나타내면 다음과 같다.
#include <iostream>
using namespace std;
void selectionSort(int arr[], int n) {
for (int i = 0; i < n - 1; ++i) {
int minIdx = i;
// Find the index of the minimum element
for (int j = i + 1; j < n; ++j) {
if (arr[j] < arr[minIdx]) {
minIdx = j;
}
}
// Swap the found minimum element with the first element
int temp = arr[minIdx];
arr[minIdx] = arr[i];
arr[i] = temp;
}
}
int main() {
int arr[] = {29, 10, 14, 37, 14};
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Before sorting: ";
for (int i = 0; i < n; ++i) cout << arr[i] << " ";
cout << endl;
selectionSort(arr, n);
cout << "After sorting: ";
for (int i = 0; i < n; ++i) cout << arr[i] << " ";
cout << endl;
return 0;
}2 - 3 삽입 정렬 (Insertion Sort)
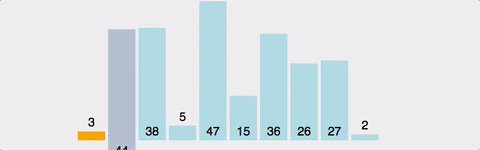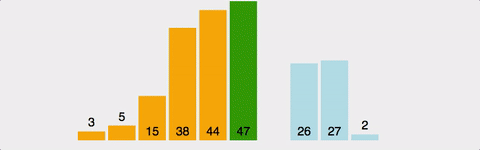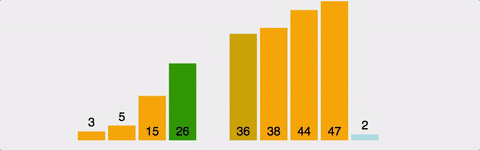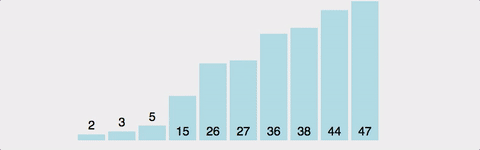
삽입정렬은 두번째 배열 그러니깐 Index 1부터 차례대로 자기보다 아래쪽으로(index 1은 index 0과 비교/ index 3은 index 2, 1, 0로 내려가면서 비교) 비교하면서 자기차리를 찾아 삽입되는 형식의 알고리즘이다. 또한 자기자리 찾으면 더 이상 아래쪽이랑은 비교하지 않기 때문에 삽입정렬은 선택정렬 보다 빠르다. 하지만 삽입정렬이 선택정렬보다 빨라도 시간복잡도는 동일하게 O(N^2) 이다.
이렇게 각기 매우 다른데 시간복잡도는 동일해서 비교를 하려면 평균적인 시나리오를 비교해야한다.
-
비유: 카드 게임에서 새 카드를 자신의 손에 맞는 위치에 끼워 넣는 것
- 배열을 왼쪽부터 차례로 순회하며, 현재 값을 정렬된 부분에 삽입한다.
-
과정:
- 첫 번째 요소는 이미 정렬된 상태로 간주.
- 두 번째 요소를 첫 번째 요소와 비교하여 적절한 위치에 배치한다.
- 세 번째 요소를 두 번째, 첫 번째 요소와 비교, 적절한 위치에 삽입한다. 이후 반복
-
시간복잡도 :
O(N^2) -
c++로 삽입 정렬을 나타내면 다음과 같다.
#include <iostream>
using namespace std;
void insertionSort(int arr[], int n) {
// 배열의 두 번째 요소부터 시작
for (int i = 1; i < n; i++) {
int key = arr[i]; // 현재 요소
int j = i - 1;
// key가 정렬된 부분의 적절한 위치에 삽입될 때까지 이동
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j]; // 요소를 한 칸 뒤로 이동
j--;
}
// key를 적절한 위치에 삽입
arr[j + 1] = key;
}
}
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++) {
cout << arr[i] << " ";
}
cout << endl;
}
int main() {
int arr[] = {12, 11, 13, 5, 6};
int n = sizeof(arr) / sizeof(arr[0]);
cout << "정렬 전 배열: ";
printArray(arr, n);
insertionSort(arr, n);
cout << "정렬 후 배열: ";
printArray(arr, n);
return 0;
}2 - 4 병합 정렬 (Merge Sort)
병합정렬은 정렬할 리스트를 반으로 쪼개나가며 좌측과 우측 리스트를 계속하여 분할해 나간 뒤 각 리스트내에서 정렬 하고 병합정렬 후 병합하는 과정을 통해 정렬하는 알고리즘이다.
병합정렬은 가장 많이 쓰이는 정렬 알고리즘 중 하나 이며 시간복잡도는 최소 O(NlogN)을 보장한다.
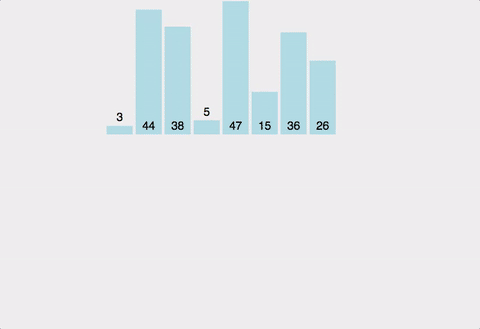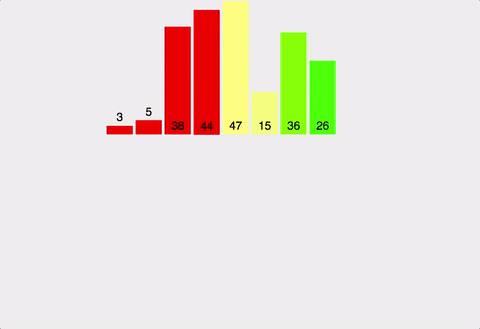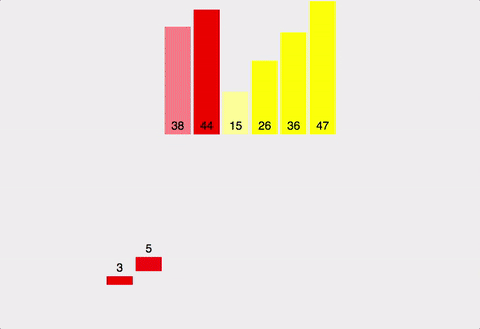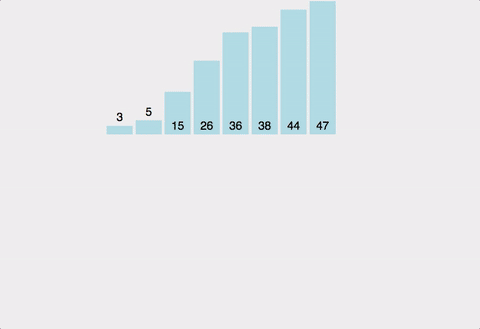
-
비유: 여러 개의 정렬된 작은 리스트를 하나로 합치는 것
- 배열을 절반으로 나누고, 각각을 정렬한 뒤 병합한다.
- 병합하면서 정렬된 상태를 유지한다.
-
과정:
- 배열을 반으로 나눈다.
- 각각의 절반을 재귀적으로 계속해서 나눈다.
- 나눈 배열을 정렬하면서 합친다.
-
시간복잡도:
O(n log n) -
c++로 병합 정렬을 나타내면 다음과 같다.
#include <iostream>
using namespace std;
void merge(int arr[], int left, int mid, int right) {
int n1 = mid - left + 1;
int n2 = right - mid;
// 동적 메모리 할당
int* L = new int[n1];
int* R = new int[n2];
// 왼쪽 및 오른쪽 배열에 값 복사
for (int i = 0; i < n1; ++i) L[i] = arr[left + i];
for (int i = 0; i < n2; ++i) R[i] = arr[mid + 1 + i];
// 병합 과정
int i = 0, j = 0, k = left;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
++i;
} else {
arr[k] = R[j];
++j;
}
++k;
}
// 왼쪽 배열의 남은 값 복사
while (i < n1) {
arr[k] = L[i];
++i;
++k;
}
// 오른쪽 배열의 남은 값 복사
while (j < n2) {
arr[k] = R[j];
++j;
++k;
}
// 동적 메모리 해제
delete[] L;
delete[] R;
}
void mergeSort(int arr[], int left, int right) {
if (left < right) {
int mid = left + (right - left) / 2;
// 분할
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
// 병합
merge(arr, left, mid, right);
}
}
int main() {
int arr[] = {12, 11, 13, 5, 6, 7};
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Before sorting: ";
for (int i = 0; i < n; ++i) cout << arr[i] << " ";
cout << endl;
mergeSort(arr, 0, n - 1);
cout << "After sorting: ";
for (int i = 0; i < n; ++i) cout << arr[i] << " ";
cout << endl;
return 0;
}2 - 5 퀵 정렬 (Quick Sort)
퀵 정렬은 속도가 빠르고 같은 시간 복잡도를(n log n) 가진 알고리즘과 비교했을 때도 가장 빠르다. 얼핏보면 병합정렬과 비슷해 보이지만 퀵 정렬은 비균등하게 분할한다. (기준이 되는 pivot 을 잘 정해야한다)
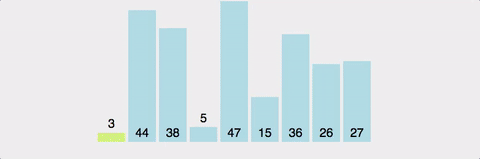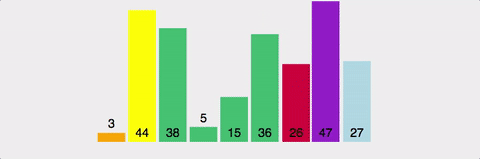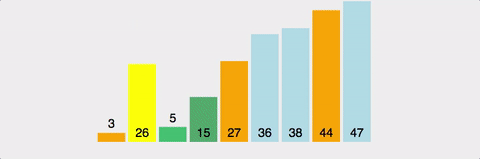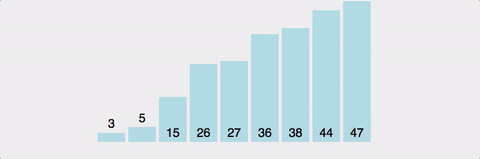
-
비유: 친구들과 줄 서서 키 순으로 정렬할 때 중간 친구를 기준으로 앞뒤로 나누는 것
- 데이터를 기준값(Pivot)을 중심으로 두 그룹으로 나누고, 각 그룹을 다시 정렬한다.
-
과정:
- 배열에서 하나의 값을 기준(Pivot)으로 선택한다.
- Pivot보다 작은 값들은 왼쪽, 큰 값들은 오른쪽 그룹으로 나눈다.
- 왼쪽과 오른쪽 그룹에서 위 과정을 재귀적으로 반복하여 정렬한다.
-
시간복잡도:
O(n log n) -
c++로 퀵 정렬을 나타내면 다음과 같다.
#include <iostream>
using namespace std;
void quickSort(int arr[], int low, int high) {
if (low < high) {
int pivot = arr[high];
int i = low - 1;
for (int j = low; j < high; ++j) {
if (arr[j] < pivot) {
++i;
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
int temp = arr[i + 1];
arr[i + 1] = arr[high];
arr[high] = temp;
int pi = i + 1;
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
int main() {
int arr[] = {10, 80, 30, 90, 40, 50, 70};
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Before sorting: ";
for (int i = 0; i < n; ++i) cout << arr[i] << " ";
cout << endl;
quickSort(arr, 0, n - 1);
cout << "After sorting: ";
for (int i = 0; i < n; ++i) cout << arr[i] << " ";
cout << endl;
return 0;
}그 외 정렬
힙정렬, 기수정렬 등이 있지만 이것은 이번 캠프 숙제를 완료하고 보충공부하러 와야겠다.
