Abstract
MIL(다중 인스턴스 학습)은 단일 클래스 레이블이 인스턴스 백에 할당되는 지도 학습의 변형입니다.
이 논문에서 우리는 bag 레이블 확률이 신경망에 의해 완전히 매개변수화되는 bag 레이블의 베르누이 분포를 학습하는 MIL 문제를 설명합니다.
또한 attention 메커니즘에 해당하는 신경망 기반 순열 불변 집계 연산자를 제안합니다.
특히, 제안된 attention-based 연산자의 적용은 bag 레이블에 대한 각 인스턴스의 기여도에 대한 insight를 제공합니다.
우리는 우리의 접근 방식이 벤치마크 MIL 데이터 세트에서 최고의 MIL 방법과 비슷한 성능을 달성하고 해석 가능성을 희생하지 않으면서 MNIST 기반 MIL 데이터 세트와 2개의 실제 조직 병리학 데이터 세트에서 다른 방법을 능가한다는 것을 경험적으로 보여줍니다.
1.Introduction
이미지 분류와 같은 일반적인 기계 학습 문제에서는 이미지가 범주(클래스)를 명확하게 나타내는 것으로 가정합니다.
그러나 많은 실제 응용 프로그램에서 여러 인스턴스가 관찰되고 범주에 대한 일반적인 설명만 제공됩니다.
이 시나리오를 다중 인스턴스 학습(MIL)(Dietterich et al., 1997; Maron & Lozano-Perez ', 1998) 또는 약하게 주석이 달린 데이터(weakly annotated data)로부터 학습(Oquab et al., 2014)이라고 합니다.
약하게 주석이 달린 데이터의 문제는 의료 영상에서 특히 분명합니다(Quellec et al.,2017년) (예, 컴퓨터 병리학, 유방 조영술 또는 CT 폐 스크리닝) 이미지가 일반적으로 단일 레이블(양성/악성)로 설명되거나 관심 영역 (ROI)이 대략적으로 제공됩니다.
MIL은 단일 클래스 레이블이 할당된 인스턴스 백을 처리합니다.
따라서 MIL의 주요 목표는 의료 진단과 같은 bag 라벨을 예측하는 모델을 학습하는 것입니다. 추가 과제는 핵심 인스턴스(Liu et al., 2012), 즉 bag 레이블을 트리거하는 인스턴스를 발견하는 것입니다.
의료 영역에서 후자의 작업은 법적 문제와 임상 실습에서의 유용성으로 인해 큰 관심을 받고 있습니다.
Bag 분류의 주요 작업을 해결하기 위해 bag 간의 유사성 활용(Cheplygina et al., 2015b), bag 수준 분류기에 추가로 제공되는 컴팩트 저차원 표현에 인스턴스를 포함하는 것과 같은 다양한 방법이 제안됩니다. 그리고 인스턴스 수준 classifier의 응답을 결합하는 단계를 포함합니다.
마지막 접근 방식만이 해석 가능한 결과를 제공할 수 있습니다
그러나 이러한 방법의 인스턴스 수준 정확도가 낮고(Kandemir & Hamprecht, 2015) 일반적으로 인스턴스 수준에서 MIL 방법 간에 불일치가 있는 것으로 나타났습니다(Cheplygina et al., 2015a).
이러한 문제는 최종 결정을 해석하기 위한 현재 MIL 모델의 유용성에 의문을 제기합니다.
이 논문에서는 해석 가능성을 MIL 접근 방식에 통합하고 유연성을 높이는 것을 목표로 하는 새로운 방법을 제안합니다. 가방 레이블에 대한 Bernoulli 분포를 사용하여 MIL 모델을 공식화하고 로그 가능도 함수를 최적화하여 훈련합니다.
우리는 대칭 함수의 기본 정리의 적용이 3단계로 구성된 백 레이블 확률(백 점수 함수)을 모델링하는 일반적인 절차를 제공한다는 것을 보여줍니다. (i) 인스턴스를 저차원 임베딩으로 변환, (ii) 순열 불변(대칭) 집계 함수, 및 (iii) 백 확률에 대한 최종 변환.
우리는 신경망(즉, 컨볼루션 및 완전 연결 레이어의 조합)을 사용하여 모든 변환을 매개변수화할 것을 제안합니다. 이는 접근 방식의 유연성을 높이고 제약이 없는 목적 함수를 최적화하여 종단 간 방식으로 모델을 훈련할 수 있습니다.
마지막으로, 우리는 최대 연산자 최대값 및 평균 연산자 평균과 같이 널리 사용되는 순열 불변 연산자를 2계층 신경망에 의해 가중치가 부여되는 훈련 가능한 가중 평균으로 대체할 것을 제안합니다.
2계층 신경망은 attention 메커니즘에 해당합니다(Bahdanau et al., 2014; Raffel & Ellis, 2015).
특히 attention 가중치를 사용하면 가능한 ROI를 강조 표시하는 데 추가로 사용할 수 있는 주요 인스턴스를 찾을 수 있습니다.
실험에서 우리는 우리 모델이 일반적인 벤치마크 MIL 데이터 세트에서 최고의 고전 MIL 방법과 동등하며 MNIST 기반 MIL 문제와 두 개의 실제 조직 병리학 이미지 데이터 세트에서 다른 방법보다 성능이 우수함을 보여줍니다.
또한 이미지 데이터 세트에서 모델이 key 인스턴스를 나타낼 수 있다는 경험적 증거를 제공합니다.
2. Methodology
2.1. 다중 인스턴스 학습(MIL)
고전적인 이진 지도 학습 문제에서 주어진 인스턴스 x ∈ R^D에 대해 대상(target) 변수 y ∈ {0, 1}의 값을 예측하는 모델을 찾는 것을 목표로 합니다.
// 입력에 대하여 출력이 0이냐 1이냐를 뜻하는듯
그러나 MIL 문제의 경우 단일 인스턴스 대신에 X = {x1, . . . , xK}와 같이 서로 종속성이나 순서를 나타내지 않습니다.
우리는 K가 bag마다 다를 수 있다고 가정합니다. 백과 관련된 단일 바이너리 레이블 Y도 있습니다.
또한, bag 내의 인스턴스에 대해 개별 레이블이 있다고 가정합니다. 즉, y1, . . . , yK 및 yk ∈ {0, 1}, k = 1, . . . , K 그러나 해당 레이블은 액세스할 수 없으며 훈련 중에 알 수 없는 상태로 유지됩니다.
MIL 문제의 가정을 다음 형식으로 다시 작성할 수 있습니다.
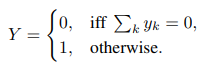
이러한 가정은 MIL 모델이 순열 불변이어야 함을 의미합니다. 또한 두 문장은 최대 연산자를 사용하여 간결한 형식으로 다시 공식화될 수 있습니다.
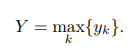
문제점:
최대 인스턴스 레이블을 기반으로 목표를 최적화하려는 모델을 학습하는 것은 적어도 두 가지 이유로 문제가 될 수 있습니다.
첫째, 모든 그라디언트 기반 학습 방법은 그라디언트 소실 문제에 직면합니다.
둘째, 이 공식은 instancelevel 분류기를 사용하는 경우에만 적합합니다.
학습 문제를 더 쉽게 만들기 위해 매개변수 θ(X) ∈ [0, 1]을 사용하여 베르누이 분포에 따라 bag 라벨이 분포하는 로그 우도 함수를 최적화하여 MIL 모델을 학습시킬 것을 제안합니다.즉, 인스턴스 X의 백이 주어지면 Y = 1의 확률
MIL 설정에서 bag 확률 θ(X)는 bag 내 인스턴스의 순서나 종속성을 가정하지 않기 때문에 순열 불변이어야 합니다.
따라서 MIL 문제는 다음 정리에 의해 주어진 단항식을 갖는 대칭 함수의 기본 정리의 특정 형태로 고려될 수 있습니다.Deepset 논문(Zaheer et al., 2017):
- 정리 1. 인스턴스 X의 집합에 대한 점수 함수 S(X) ∈ R은 다음 형식으로 분해될 수 있는 경우에만 대칭 함수입니다.(즉, X의 요소에 대한 순열 불변)
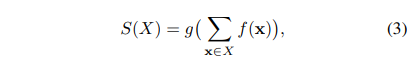여기서 f와 g는 적절한 변환입니다.
이 정리는 (3)에 주어진 분해를 사용하여 백 확률을 모델링하기 위한 일반적인 전략을 제공합니다. 합 대신 최대를 사용한 유사한 분해는 다음 정리에 의해 제공됩니다(Qi et al., 2017).
- 정리 2. 모든 ε > 0에 대해 하우스도르프 연속 대칭 함수 S(X) ∈ R은 g(max_x∈X f(x)) 형식의 함수로 임의로 근사할 수 있습니다. 여기서 max는 요소별 벡터 최대값입니다. 연산자와 f 및 g는 연속 함수입니다. 즉,
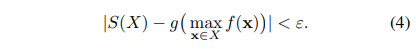
정리 1과 2의 차이점은 전자는 보편적인 분해이고 후자는 임의의 근사치를 제공한다는 것입니다.
그럼에도 불구하고, 그들은 둘 다 인스턴스 백을 분류하기 위한 일반적인 3단계 접근 방식을 공식화합니다. (i) 함수 f를 사용한 인스턴스 변환, (ii) 대칭(순열 불변) 함수 σ를 사용하여 변환된 인스턴스 조합, (iii) 함수 g를 사용하여 f로 변환된 결합된 인스턴스의 변환.
마지막으로, 점수 함수의 표현성은 f 및 g에 대한 함수 클래스의 선택에 의존합니다.
MIL 문제 공식화에서 두 정리의 점수 함수는 확률 θ(X)이고 순열 불변 함수 σ는 MIL 풀링이라고 합니다. 함수 f, g 및 σ의 선택은 레이블 확률 모델링에 대한 특정 접근 방식을 결정합니다. 주어진 MIL 연산자에 대해 두 가지 주요 MIL 접근 방식이 있습니다.
- (i) 인스턴스 level 접근: 변환 f는 각 인스턴스에 대한 점수를 반환하는 인스턴스 level 분류기입니다. 그런 다음 MIL 풀링에 의해 개별 점수를 집계하여 θ(X)를 얻습니다. 함수 g는 항등 함수입니다.
- (ii) 임베딩 level 접근: 함수 f는 인스턴스를 저차원 임베딩에 매핑합니다. MIL 풀링은 백의 인스턴스 수에 따라 달라지는 백 표현을 얻는 데 사용됩니다. 백 표현은 bag level 분류기에 의해 추가 처리되어 θ(X)를 제공합니다.
(Wang et al., 2016)은 bag level 분류 성능 측면에서 후자의 접근 방식이 바람직하다고 주장합니다.
개별 레이블을 알 수 없기 때문에 인스턴스 level 분류기가 불충분하게 훈련되어 최종 예측에 추가 오류가 발생할 수 있다는 위협이 있습니다.
임베딩 level 접근 방식은 백의 공동 표현을 결정하므로 백 level 분류기에 추가적인 편향을 도입하지 않습니다.
반면에 인스턴스 level 접근 방식은 핵심 인스턴스, 즉 백 레이블을 트리거하는 인스턴스를 찾는 데 사용할 수 있는 점수를 제공합니다.
Liu et al. (2012) 논문에서는 주요 사례를 성공적으로 감지하는 모델이 더 나은 백 라벨 예측을 달성할 가능성이 더 높다는 것을 보여줄 수 있었습니다.
우리는 새로운 MIL 풀링을 사용하여 해석 가능하도록 임베딩 level 접근 방식을 수정하는 방법을 보여줍니다.
2.2. MIL with Neural Networks(신경망을 사용한 MIL)
고전적인 MIL 문제에서 인스턴스는 추가 처리가 필요하지 않은 기능으로 표현된다고 가정합니다. 즉, f는 identity(항등함수)입니다.
그러나 이미지 또는 텍스트 분석과 같은 일부 작업의 경우 특징 추출의 추가 단계가 필요합니다.
또한 정리 1과 2는 충분히 유연한 함수 클래스에 대해 순열 불변 점수 함수를 모델링할 수 있음을 나타냅니다.
따라서 우리는 k번째 인스턴스를 저차원 임베딩으로 변환하는 매개변수 ψ가 있는 신경망 fψ(·)에 의해 매개변수화된 변환 클래스를 고려합니다. h_k = fψ(x_k), 여기서 h_k ∈ H 는 H = [0,1] 인스턴스 기반 접근 방식의 경우 // 임베딩 기반 접근 방식의 경우 H = R^M입니다.
결국 매개변수 θ(X)는 변환 gφ : H^K → [0, 1]에 의해 결정됩니다.
인스턴스 기반 접근 방식에서 변환 gφ는 단순히 아이덴티티(항등함수)인 반면, 임베딩 기반 접근 방식에서는 매개변수 φ가 있는 신경망에 의해 매개변수화될 수도 있습니다.
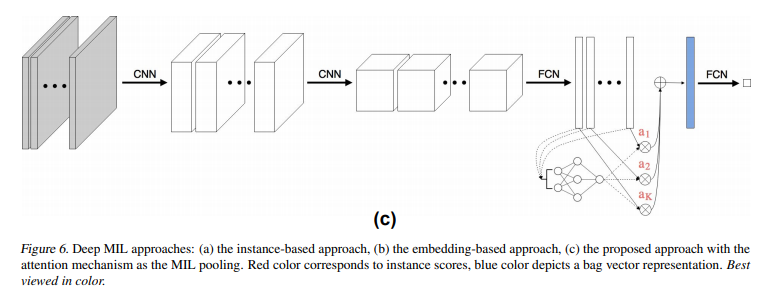
전자의 접근 방식은 부록의 그림 6(a)에, 후자는 그림 6(b)에 나와 있습니다.
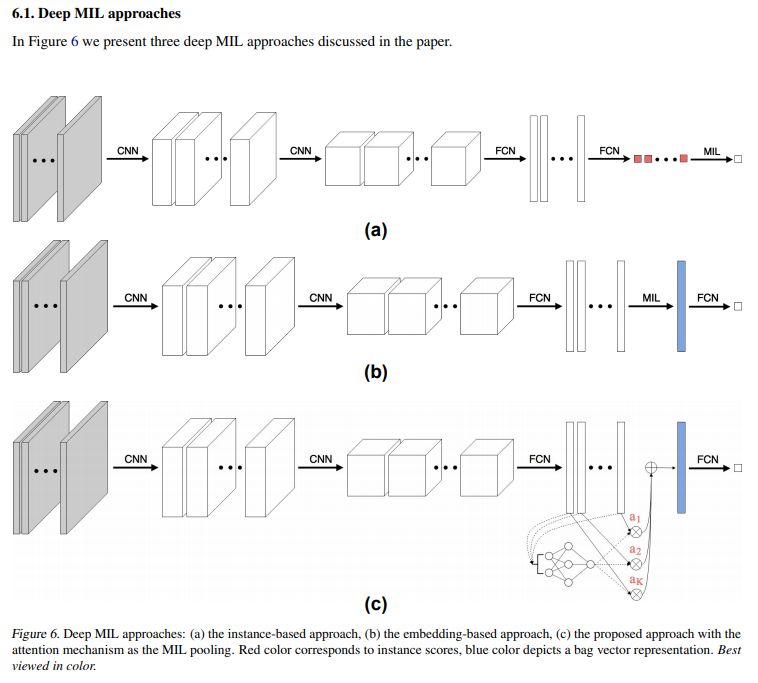
신경망을 사용하여 모든 변환을 매개변수화하는 아이디어는 전체 접근 방식이 임의로 유연할 수 있고 역전파를 통해 종단 간 훈련이 가능하기 때문에 매우 매력적입니다. 유일한 제한 사항은 MIL 풀링이 미분 가능해야 한다는 것입니다.(중요 이유를 알아보자)
2.3. MIL pooling
MIL 문제를 공식화하려면 MIL 풀링 σ가 순열 불변이어야 합니다.
정리 1과 2에서 볼 수 있듯이 점수(score) 함수(즉, bag 확률)가 대칭 함수, 즉 최대 연산자가 되도록 보장하는 두 개의 MIL 풀링 연산자가 있습니다.
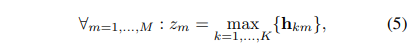
평균 연산자:
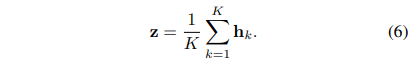
사실, 볼록 최대 연산자(예: log-sum-exp)와 같은 다른 연산자를 사용할 수 있습니다. (Ramon & De Raedt,2000), Integrated Segmentation and Recognition (Keeler t al., 1991), noisy-or (Maron & Lozano-Perez, 1998) and noisy-and (Kraus et al., 2016).
이러한 MIL 풀링 연산자는 정리 2에서 최대값을 대체할 수 있으며 증명은 유사한 방식으로 따를 것입니다(최대 연산자에 대한 자세한 증명은 (Qi et al., 2017)의 보충 참조!!!!). 이러한 연산자는 모두 미분할 수 있으므로 심층 신경망 아키텍처에서 MIL 풀링 계층으로 쉽게 사용할 수 있습니다.
2.4. Attention-based MIL pooling
이전 섹션에서 언급한 모든 MIL 풀링 연산자는 미리 정의되어 있고 훈련할 수 없다는 분명한 단점이 있습니다.
예를 들어, max-operator는 인스턴스 기반 접근 방식에서는 좋은 선택이 될 수 있지만 임베딩 기반 접근 방식에는 부적절할 수 있습니다.
마찬가지로 평균 연산자는 인스턴스 점수를 집계하기 위한 잘못된 MIL 풀링이지만 bag 표현을 계산하는 데 성공할 수 있습니다.
따라서 유연하고 적응적인 MIL 풀링은 Task 및 데이터에 맞게 조정하여 잠재적으로 더 나은 결과를 얻을 수 있습니다.
이상적으로는 이러한 MIL 풀링도 해석 가능해야 하며 이는 섹션 2.3에서 언급한 모든 연산자에서 누락된 특성입니다.
Attention mechanism
가중치가 신경망에 의해 결정되는 인스턴스(저차원 임베딩)의 가중 평균을 사용할 것을 제안합니다.
또한 가중치의 합이 1이 되어야 bag 크기에 변함이 없습니다.
가중 평균은 임베딩과 함께 가중치가 f 함수의 일부인 정리 1의 요구 사항을 충족합니다.
H = {h_1, . . . , h_K}가 K 임베딩의 백일 경우 다음 MIL 풀링을 제안합니다.
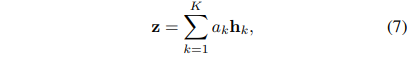
where:
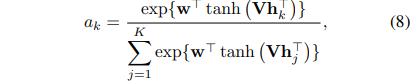
여기서 w ∈ R^L×1 및 V ∈ R^L×M은 매개변수입니다.
또한, 쌍곡선 탄젠트 tanh(·) 요소별 비선형성을 활용하여 적절한 기울기 흐름을 위해 음수 및 양수 값을 모두 포함합니다.
제안된 구성을 통해 인스턴스 간의 (비)유사성을 발견할 수 있습니다.
흥미롭게도 제안된 MIL 풀링은 attention 메커니즘의 버전에 해당합니다(Lin et al.,A structured self-attentive sentence embedding. 2017; Raffel & Ellis,Feed-forward networks with attention can solve some long-term memory problems. 2015).
주요 차이점은 일반적으로 attention 메커니즘에서 모든 인스턴스가 순차적으로 종속되는 반면 여기에서는 모든 인스턴스가 독립적이라고 가정한다는 것입니다.
따라서 자연스럽게 발생하는 질문은 attention 메커니즘이 인스턴스 간의 순차적 종속성 없이 작동할 수 있는지, 그리고 평균 연산자를 학습하지 않는지 여부입니다.
우리는 실험에서 이 문제를 다룰 것입니다.
Gated attention mechanism
또한 tanh(·) 비선형성은 복잡한 관계를 학습하는 데 비효율적일 수 있습니다.
우리의 우려는 tanh(x)가 x ∈ [−1, 1]에 대해 거의 선형이라는 사실에서 비롯되며, 이는 인스턴스 간의 학습된 관계의 최종 표현성을 제한할 수 있습니다.
따라서 다음을 생성하는 tanh(·) 비선형성과 함께 게이팅 메커니즘(Dauphin et al., 2016)을 추가로 사용할 것을 제안합니다.
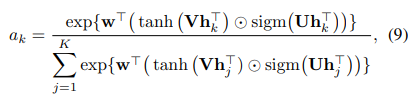
여기서 U ∈ R^L×M은 매개변수이고, 곱셈(원)은 요소별 곱셈이고 sigm(·)은 시그모이드 비선형성입니다. 게이팅 메커니즘은 잠재적으로 tanh(·)의 번거로운 선형성을 제거하는 학습 가능한 비선형성을 도입합니다.
Flexibility(유연성)
원칙적으로 제안된 attention 기반 MIL 풀링은 백 내의 인스턴스에 서로 다른 가중치를 할당할 수 있으므로 백의 최종 표현은 백 level 분류기에 매우 유익할 수 있습니다.
즉, key instances를 찾을 수 있어야 합니다.
더욱이, 신경망에 의해 매개변수화된 변환 f 및 g와 함께 attention 기반 MIL 풀링을 적용하면 전체 모델을 완전히 미분 및 적응(adaptive)할 수 있습니다.
이 두 가지 사실로 인해 제안된 MIL 풀링은 임의의 순열 불변 score 함수를 모델링할 수 있는 잠재적으로 매우 유연한 연산자입니다.
심층 MIL 모델과 함께 제기된 주의 메커니즘은 앱의 그림 6(c)에 나와 있습니다.
Interpretability(해석 가능성)
이상적으로는 양수 레이블(Y = 1)의 경우 레이블 yk = 1(key 인스턴스)을 가질 가능성이 있는 인스턴스에 높은 주의 가중치를 할당해야 합니다.
즉, attention 메커니즘을 사용하면 제공된 결정을 인스턴스 수준 레이블 측면에서 쉽게 해석할 수 있습니다.
사실 어텐션 네트워크는 인스턴스 기반 분류기처럼 점수를 제공하지 않지만 이에 대한 프록시로 간주될 수 있습니다.
attention 기반 MIL 풀링은 인스턴스 level 접근 방식과 임베딩 level 접근 방식을 연결합니다.
예를 들어, 계산 병리학에서 실제적인 관점에서, 의사에게 최종 진단과 함께 ROI를 제공하는 것이 바람직합니다. 따라서 attention 메커니즘은 실제 응용에서 잠재적으로 큰 관심을 끌 것입니다.
3. Related
MIL pooling
일반적으로 MIL 접근 방식은 평균 풀링 또는 최대 풀링을 사용하지만 후자가 대부분 사용됩니다.(Feng & Zhou, 2017; Pinheiro & Collobert, 2015; Zhu et al., 2017).
두 연산자 모두 훈련이 불가능하여 잠재적으로 적용 가능성이 제한됩니다.
노이즈와 같은 전역 적응 매개변수를 포함하는 MIL 풀링 연산자가 있지만 유연성이 제한됩니다.(Kraus et al., 2016)
우리는 새로운 인스턴스에 적응하는 완전히 훈련 가능한 MIL 풀링을 제안합니다.
MIL with neural networks
MIL에 대한 고전적인 작업에서는 인스턴스가 미리 계산된 feature로 표현되고 추가 feature 추출을 적용할 필요가 거의 없다고 가정합니다.
그럼에도 불구하고 MIL에서 완전 연결된 신경망을 활용하는 최근 연구는 이것이 여전히 유익할 수 있음을 보여줍니다(Wang et al., 2016).
유사하게, 컴퓨터 비전에서 딥 러닝과 결합된 MIL의 아이디어는 최종 정확도를 크게 향상시킵니다(Oquab et al., 2014).
이 논문에서 우리는 역전파에 의해 종단 간 훈련될 수 있는 유연한 변환 클래스를 적용할 수 있기 때문에 이 연구 라인을 따릅니다.
MIL and attention
Attention 메커니즘은 이미지 캡션(Xu et al., 2015) 또는 텍스트 분석(Bahdanau et al., 2014; Lin et al., 2017)을 위한 딥 러닝에서 널리 사용됩니다.
MIL 문제의 맥락에서 이것은 거의 사용되지 않았고 매우 제한된 형태로만 사용되었습니다.
(Pappas & Popescu-Belis, 2014)에서는 주의 기반 MIL이 제안되었지만 attention 가중치는 보조 선형 회귀 모델의 매개변수로 훈련되었습니다.
이 아이디어는 더욱 확장되었고 선형 회귀 모델은 단일 출력을 갖는 1계층 신경망으로 대체되었습니다(Pappas & Popescu-Belis, 2017).
Attention 기반 MIL 연산자는 최근(Qi et al., 2017)에서 사용되었지만 내적(dot product)을 사용하여 attention를 계산했으며 최대 연산자보다 성능이 좋지 않았습니다.
여기에서 우리는 MIL 연산자를 학습하기 위해 2계층 신경망을 사용할 것을 제안하고 일반적으로 사용되는 MIL 풀링 연산자보다 성능이 우수함을 보여줍니다.
MIL for medical imaging(의료 영상용 MIL)
MIL은 수십억 개의 픽셀로 구성된 전체 이미지를 처리하는 것이 계산적으로 불가능한 의료 영상에 완벽하게 들어맞는 것 같습니다.
더욱이 의료 영역에서는 픽셀 수준의 주석을 얻는 것이 매우 어렵기 때문에 사용 가능한 데이터의 수가 크게 줄어듭니다.
따라서 의료 이미지를 더 작은 패치로 나누고 단일 레이블이 있는 가방으로 간주할 수 있습니다(Quellec et al., 2017).
이 아이디어는 패치가 악성 변화를 나타내는 것으로 여겨지는 세포에 해당할 수 있는 컴퓨터 조직병리학에서 큰 관심을 끌고 있습니다(Sirinukunwattana et al., 2016).
가우시안 프로세스(Kandemir et al., 2014; 2016) 또는 인스턴스 클래스를 결정하기 위한 신경망 및 EM 알고리즘을 사용한 2단계 접근(Hou et al., 2016)과 같은 조직병리학 데이터에 다양한 MIL 접근 방식이 사용되었습니다.
의료 영상에서 MIL 방법의 다른 적용은 유방 조영술(결절) 분류(Zhu et al., 2017) 및 현미경 세포 검출(Kraus et al., 2016)입니다. 이 논문에서 우리는 제안된 attention 기반 심층 MIL 접근 방식이 최종 진단을 제공할 뿐만 아니라 조직 병리학 슬라이드에서 ROI를 나타내는 데에도 사용될 수 있음을 보여줍니다.
4. Experiments
실험에서 우리는 제안된 접근 방식을 평가하는 것을 목표로 합니다. 신경망과 (게이트된) attention 기반 풀링 레이어('Attention' 및 'Gated-Attention')로 매개변수화된 MIL 모델입니다. 5개의 MIL 벤치마크 데이터 세트(MUSK1, MUSK2, FOX, TIGER, ELEPHANT), MNIST 기반 이미지 데이터 세트(MNIST-BAGS) 및 2개의 실제 조직 병리학 데이터 세트(BREAST CANCER, COLON CANCER)와 같은 다양한 MIL 데이터 세트에 대한 접근 방식을 평가합니다. 우리는 실험에서 두 가지 연구 질문을 확인하기를 원합니다. (i) 우리의 접근 방식이 최고의 성능을 달성하거나 최고의 성능을 발휘하는 방법과 비교할 수 있는지, (ii) 우리의 방법이 key instances 또는 ROI를 나타내는 주의 가중치를 사용하여 해석 가능한 결과를 제공할 수 있는 경우.
공정한 비교를 위해 일반적인 평가 방법론, 즉 10겹 교차 검증(10-fold-cross-validation)및 실험당 5회 반복을 사용합니다. MNIST-BAGS의 경우 훈련 세트와 테스트 세트로 고정 분할을 사용합니다. 테스트 백을 만들기 위해 MNIST 테스트 세트에서 이미지만 샘플링했습니다. 훈련 중에는 MNIST 훈련 세트의 이미지만 사용했습니다.
모든 실험에 대해 개별 데이터 세트에서 높은 분류 성능을 보인 수정된 버전의 모델을 사용합니다(Wang et al., 2016; LeCun et al., 1998; Sirinukunwattana et al., 2016).
MIL 풀링 계층은 모델의 마지막 계층 앞에 위치하거나(임베디드 기반 접근 방식) 모델의 마지막 계층 뒤에 위치합니다(인스턴스 기반 접근 방식). Attention 기반 MIL 풀링 레이어가 사용되는 경우 V의 매개변수 수는 유효성 검사 세트를 사용하여 결정되었습니다.
우리는 다음 dimensions(L)를 테스트했습니다: 64, 128 및 256. 다른 치수는 모델의 성능에 약간의 변화만 가져왔습니다.
게이트 어텐션 메커니즘을 사용하는 레이어의 경우 V와 U는 동일한 수의 매개변수를 갖습니다. 마지막으로 모든 레이어는 Glorot & Bengio(2010)에 따라 초기화되었고 바이어스는 0으로 설정되었습니다.
MIL 벤치마크 데이터 세트에서 다양한 MIL 방법에 대한 접근 방식을 비교합니다.
이미지 데이터 세트에서 우리의 방법은 인스턴스 level 및 임베딩 level 신경망과 일반적으로 사용되는 MIL 풀링 레이어(최대 및 평균)와 비교됩니다.
다음에서는 '인스턴스+최대/평균' 및 '임베딩+최대/평균'을 사용하여 컨볼루션 계층과 완전 연결 계층으로 구성된 네트워크를 나타냅니다.
네트워크가 완전히 연결된 계층으로만 구성된 것과 대조적으로 'mi-Net' 및 'MI-Net'이라고 합니다(Wang et al., 2016).
MNIST-BAGS에는 (MI-SVM)이라는 SVM 기반 MIL 모델이 포함되어 있습니다.
합리적인 시간 내에 모델을 훈련(초매개변수 검색 및 5회 10배 교차 검증 절차 포함)할 수 없기 때문에 조직병리학 데이터 세트에 대한 MI-SVM 결과를 제시하지 않습니다.
백 level 성능을 비교하기 위해 분류 정확도, 정밀도, 재현율, F-score 및 수신기 작동 특성 곡선(AUC) 아래 영역과 같은 메트릭을 사용합니다.
4.1. Classical MIL datasets
Details(세부정보)
첫 번째 실험에서는 우리의 접근 방식이 역사적으로 중요한 벤치마크 데이터 세트에서 최고의 MIL 방법과 경쟁할 수 있는지 확인하는 것을 목표로 합니다.
5개의 데이터 세트에는 모두 미리 계산된 기능과 소수의 인스턴스 및 백만 포함되어 있으므로 신경망은 적합하지 않을 가능성이 높습니다.
먼저 약물 활성(MUSK1 및 MUSK2)을 예측합니다.
분자는 하나 이상의 구조가 표적 결합 부위에 결합하는 경우에만 원하는 약물 효과를 나타냅니다.
분자는 여러 모양을 취할 수 있기 때문에 bag은 같은 분자에 속하는 모양으로 구성됩니다(Dietterich et al., 1997).
나머지 3개의 데이터 세트인 ELEPHANT, FOX 및 TIGER에는 이미지에서 추출한 특징이 포함되어 있습니다. 각 백은 이미지의 세그먼트 세트로 구성됩니다. 각 범주에 대해 포지티브 백은 관심 동물이 포함된 이미지이고 네거티브 백은 다른 동물이 포함된 이미지입니다(Andrews et al., 2003). 각 데이터 세트의 백, 인스턴스 및 특징 수에 대한 자세한 정보는 부록의 섹션 6.3을 참조하십시오.
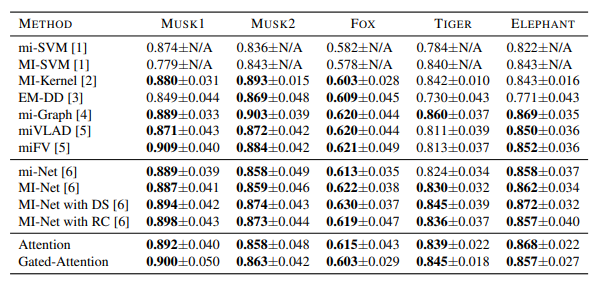
표 1에는 실험에 사용된 5개의 벤치마크 MIL 데이터 세트에 대한 일반적인 설명이 나와 있습니다.
Table 5와 6은 각각 임베딩 기반 모델과 인스턴스 기반 모델의 아키텍처를 보여준다. 완전 연결 계층을 'fc'로 표시하고 출력 은닉 유닛의 수는 대시 뒤에 제공됩니다. ReLU 비선형성이 사용되었습니다. 표 7에는 최적화(학습) 절차의 세부 사항이 나와 있습니다. 가장 높은 검증 성능을 달성한 모델 선택 절차에 따라 결정된 하이퍼파라미터 값을 제공합니다.
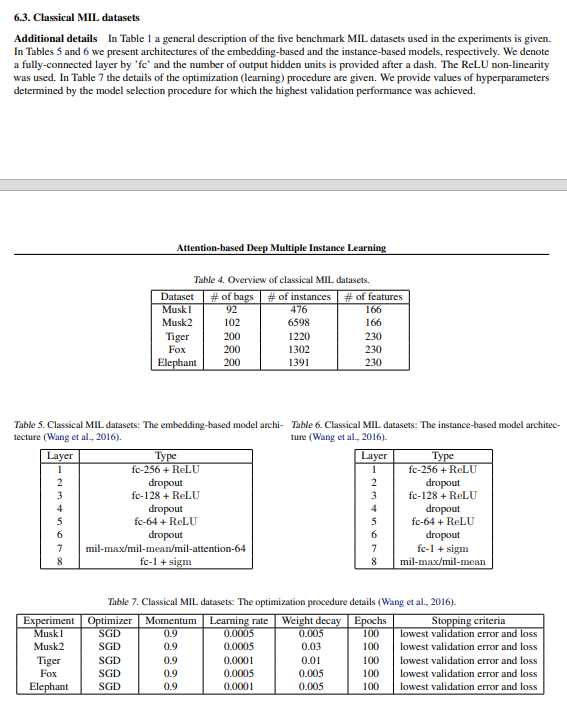
우리의 실험에서 우리는 MI-Net 모델에서와 동일한 아키텍처, 옵티마이저 및 하이퍼파라미터를 사용합니다(Wang et al., 2016).
표 1. 기존 MIL 데이터 세트에 대한 결과. 실험은 5회 실행되었으며 분류 정확도의 평균(±평균의 표준 오차)이 보고됩니다. [1] (Andrews et al., 2003), [2] (Gartner et al., 2002), [3] (Zhang & Goldman, 2002) [4] (Zhou et al., 2009) [5] (Wei et al., 2017) [6] (Wang et al., 2016)
Results and discussion
실험 결과는 표 1에 나와 있습니다.
우리의 접근 방식(Attention 및 GatedAttention)은 최고 성능의 기존 MIL 방법과 유사합니다(평균의 표준 오차에 유의).
4.2. MNIST-bags
Details(세부정보)
기존 MIL 벤치마크 데이터 세트의 주요 단점은 인스턴스가 미리 계산된 기능으로 표시된다는 것입니다.
보다 도전적인 시나리오를 고려하기 위해 잘 알려진 MNIST 이미지 데이터 세트를 사용하여 생성된 데이터 세트를 조사할 것을 제안합니다.
백은 MNIST 데이터 세트에서 가져온 28 × 28 회색조 이미지의 임의 번호로 구성됩니다.
bag에 있는 이미지의 수는 가우스 분포이며 가장 가까운 정수 값을 취합니다.
bag에 '9'라는 라벨이 있는 이미지가 하나 이상 포함되어 있는 경우 가방에 긍정적인 라벨이 부여됩니다.
'7'이나 '4'와 혼동하기 쉽기 때문에 '9'를 선택했습니다.
예측 성능에 대한 학습 세트의 백 수와 백당 평균 인스턴스 수의 영향을 조사합니다.
평가하는 동안 고정된 수의 1000개의 테스트 백을 사용합니다.
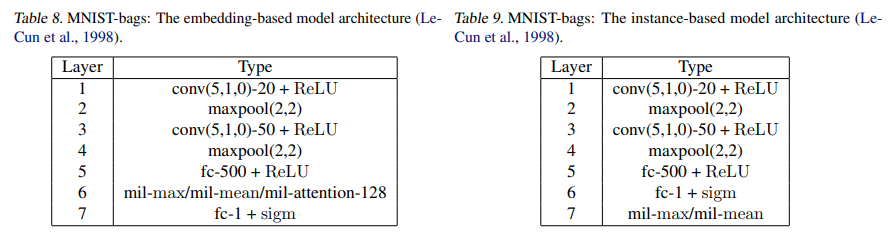
모든 실험에서 LeNet5 모델이 사용되었습니다(LeCun et al., 1998). 부록의 표 8과 9를 참조하십시오.
모델은 Adam 최적화 알고리즘으로 훈련됩니다(Kingma & Ba, 2014). β1 및 β2에 대한 기본 매개변수를 유지합니다(부록의 표 10 참조).
또한 우리의 방법을 원시 픽셀 기능에 가우시안 커널을 사용하는 SVM 기반 MIL 방법(MI-SVM)(Andrews et al., 2003)과 비교합니다.
실험에서 우리는 각각 다른 수의 평균 bag 크기, 즉 10, 50 및 100과 분산 2, 10, 20을 사용합니다.
또한 50, 100, 150, 200, 300, 400, 500과 같이 다양한 수의 훈련 가방을 사용합니다.
이러한 다양한 설정을 통해 다양한 훈련 가방 수와 다양한 인스턴스 수가 MIL 모델에 미치는 영향을 확인할 수 있습니다.
우리는 평균 및 최대 MIL 풀링을 사용하여 신경망(LeNet5)으로 매개변수화된 인스턴스 기반 및 임베딩 기반 접근 방식을 비교합니다.
평가 지표로 AUC를 사용합니다.
Results and discussion(결과 및 토론)
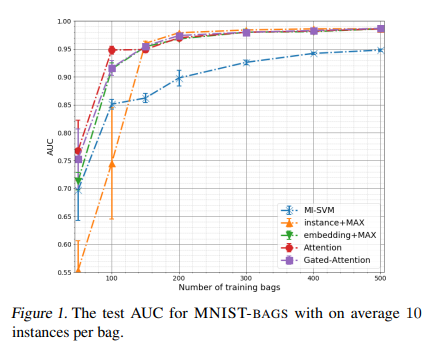
10, 50, 100에 해당하는 평균 가방 크기에 대한 AUC의 결과는 각각 그림 1, 2, 3에 나와 있으며 자세한 결과는 부록에 나와 있습니다.
실험의 결과는 다음과 같습니다. 첫째, 제안된 주의 기반 심층 MIL 접근 방식은 작은 표본 크기 영역에서 다른 방법보다 훨씬 더 나은 성능을 보입니다.
또한, bag당 약 10개의 인스턴스에 대해 50-150개의 가방(그림 1 참조) 또는 bag에 평균 50개의 인스턴스(그림 2 참조)의 경우 50-100개의 가방에 해당하는 학습 세트의 작은 유효 크기가 있는 경우, 우리의 방법은 여전히 다른 모든 방법보다 훨씬 더 높은 AUC를 달성합니다.
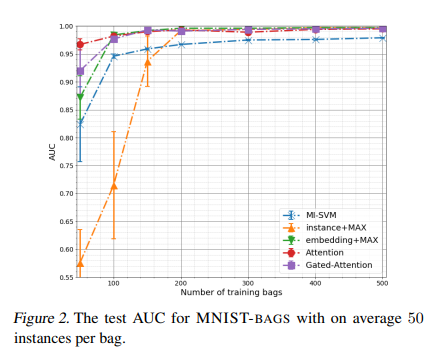
둘째, 우리는 우리의 접근 방식이 큰 유효 표본 크기를 제외한 모든 경우에 SVM 기반 접근 방식보다 더 유연하고 더 나은 결과를 얻었음을 알 수 있습니다(그림 3 참조).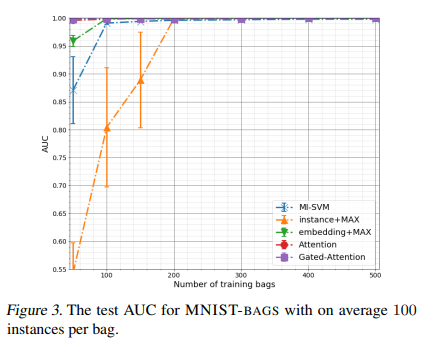
셋째, 임베딩 기반 모델이 인스턴스 기반 모델보다 더 나은 성능을 보였다. 그러나 충분한 수의 훈련 이미지(가방당 훈련 가방 및 훈련 인스턴스 수)의 경우 모든 모델이 매우 유사한 결과를 얻습니다.
넷째, 평균 연산자는 최대 연산자보다 훨씬 더 나쁜 성능을 보입니다.
그러나 평균 연산자를 사용하는 임베딩 기반 모델은 결국 최상의 값으로 수렴되지만 항상 최대 값보다 나중에 수렴됩니다. 자세한 내용은 부록의 섹션 6.4를 참조하십시오.
이 실험의 결과는 작은 표본 크기 체제에 대해 우리의 접근 방식이 다른 접근 방식보다 더 낫다는 것을 나타냅니다.
Attention은 역전파 동안 그래디언트 업데이트 필터 역할을 하기 때문에(Wang et al., 2017) 더 높은 가중치를 가진 인스턴스는 인스턴스의 인코더 네트워크를 학습하는 데 더 많이 기여할 것입니다.
의료 영상 문제에는 소수의 사례만 포함되기 때문에 이것은 특히 중요합니다.
일반적으로 MIL 가정에서는 음수 백의 모든 인스턴스가 음수임을 명시하기 때문에 백에 더 많은 인스턴스가 있을수록 MIL 작업이 더 쉬워집니다.
예를 들어, MNIST-bags 데이터 세트에서 크기가 100인 음성 가방에는 클래스당 약 11개의 음성 예제가 포함됩니다.
마지막으로 그림 4에서 주의 메커니즘의 예시적인 결과를 제시합니다.
이 예에서 가방은 13개의 이미지로 구성됩니다. 각 숫자에 대해 해당 attention 가중치는 훈련된 네트워크에서 제공됩니다. 가방은 긍정적으로 올바르게 예측되고 모든 9가 올바르게 강조 표시됩니다. 따라서 attention 메커니즘은 예상대로 작동합니다. 부록에 더 많은 예가 나와 있습니다.
4.3. Histopathology datasets
Details(세부정보)
헤마톡실린 및 에오신(H&E) 스테인드 전체 슬라이드 이미지에서 암 영역의 자동 감지는 임상 관련성이 높은 작업입니다.
현재 supervised되는 접근 방식은 픽셀 수준 주석을 사용합니다(Litjens et al., 2017).
그러나 데이터 준비는 병리학자의 많은 시간을 필요로 하여 일상에 큰 지장을 줍니다.
따라서 약한 레이블로 작업하는 성공적인 솔루션은 병리학자의 작업량을 줄이는 데 큰 도움이 될 것입니다.
다음에서는 유방암 데이터 세트(BREAST CANCER)(Gelasca et al., 2008)와 결장암 데이터 세트(COLON CANCER)(Sirinukunwattana et al., 2016)의 약하게 표지된 실제 조직 병리학 이미지를 분류하는 두 가지 실험을 수행합니다.
유방암은 약하게 레이블이 지정된 896 × 768 H&E 이미지 58개로 구성됩니다. 이미지에 유방암 세포가 있으면 악성으로 분류되고 그렇지 않으면 양성으로 분류됩니다. 모든 이미지를 32 × 32 패치로 나눕니다. 그 결과 bag당 672개의 패치가 생성됩니다. 75% 이상의 흰색 픽셀이 포함된 패치는 폐기됩니다.
대장암은 100개의 H&E 이미지로 구성됩니다. 이미지는 정상 및 악성 영역의 다양한 조직 모양에서 비롯됩니다. 모든 이미지에 대해 각 세포의 대부분의 핵이 표시되었습니다. 총 22,444개의 핵이 관련 클래스 레이블, 즉 상피, 염증, 섬유아세포 및 기타를 포함합니다. bag은 27×27 패치로 구성됩니다. 또한 백에 상피 등급의 핵이 하나 이상 포함되어 있으면 백에 긍정적인 레이블이 부여됩니다.
결장암은 상피 세포에서 기원하기 때문에 상피 세포에 태그를 지정하는 것은 임상 관점에서 매우 관련이 있습니다(Ricci-Vitiani et al., 2007).
두 데이터 세트에 대해 변환 f를 위해 (Sirinukunwattana et al., 2016)에서 제안한 모델을 사용합니다. 모든 모델은 Adam 최적화 알고리즘으로 훈련되었습니다(Kingma & Ba, 2014). 두 데이터 세트의 제한된 데이터 샘플로 인해 과적합을 방지하기 위해 데이터 증강을 수행했습니다. 자세한 내용은 부록을 참조하십시오.
Results and discussion(결과 및 토론)
유방암 및 대장암에 대한 결과를 각각 표 2 및 3에 제시합니다.
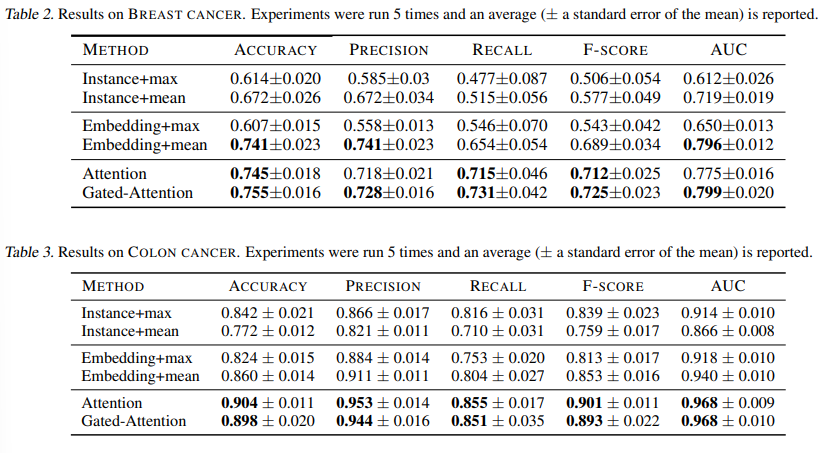
첫째, 얻은 결과가 MNIST-BAGS 실험에서 우리의 접근 방식이 다른 모든 방법보다 성능이 우수하다는 결과를 확인시켜줍니다. MNIST-BAGS의 소규모 표본 크기 체제에서 특히 볼 수 있는 추세입니다.
놀랍게도, 최대 풀링을 사용한 임베딩 기반 방법은 유방암에서 거의 완전히 실패했지만 일반적으로 이 데이터 세트는 슬라이드의 높은 가변성과 적은 수의 사례로 인해 어렵습니다.
제안된 방법은 가장 정확할 뿐만 아니라 가장 높은 재현율을 받았습니다.
위음성은 환자 사망을 포함한 심각한 결과를 초래할 수 있기 때문에 높은 회수율은 의료 영역에서 특히 중요합니다.
또한 BREAST CANCER에서는 gated-attention 메커니즘이 plain Attention 메커니즘보다 더 잘 수행되는 반면 이 두 가지는 COLON CANCER에서 유사하게 작동합니다.
결국 우리는 ROI 제공에 있어 주의 메커니즘의 유용성을 제시합니다.
그림 5에서 우리는 (대부분) 단일 세포를 포함하는 패치로 분할된 조직병리학 이미지를 보여줍니다.
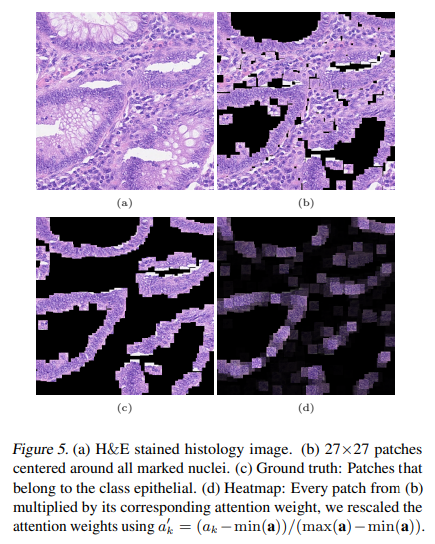
패치에 해당 attention 가중치를 곱하여 히트맵을 만듭니다. 훈련 중에는 이미지 수준 주석만 사용되지만 그림 5(d)의 히트맵과 그림 5(c)의 정답 간에 상당한 일치가 있습니다. 또한 인스턴스 기반 분류기는 (Kandemir & Hamprecht, 2015)에서 논의된 인스턴스 기반 접근 방식의 낮은 인스턴스 정확도를 확인하는 긍정적 패치(부록의 그림 10(e) 참조)의 작은 하위 집합만 선택하는 경향이 있음을 알 수 있습니다.
더 많은 예를 보려면 부록을 참조하십시오.
얻은 결과는 제안된 접근 방식이 높은 예측 성능을 달성하고 ROI를 적절하게 강조할 수 있음을 다시 확인합니다. 또한 주의 가중치를 사용하여 신뢰할 수 있는 히트맵을 생성할 수 있습니다.
5. Conclusion
이 논문에서 우리는 신경망에 의해 완전히 매개변수화되는 유연하고 해석 가능한 MIL 접근 방식을 제안했습니다. 대칭 함수의 기본 정리 측면에서 순열 불변 백 score 함수를 모델링하기 위한 딥 러닝의 유용성을 설명했습니다. 또한 (게이트) attention 메커니즘을 기반으로 하는 훈련 가능한 MIL 풀링을 제시했습니다. 우리는 5개의 MIL 데이터 세트, 하나의 이미지 말뭉치 및 2개의 실제 조직 병리학 데이터 세트에서 우리의 방법이 가장 성능이 좋은 방법과 동등하거나 다른 평가 메트릭 측면에서 최고를 수행한다는 것을 경험적으로 보여주었습니다. 또한 우리의 접근 방식이 많은 실제 응용 프로그램에서 매우 중요한 ROI를 제시함으로써 결정에 대한 해석을 제공한다는 것을 보여주었습니다.
우리는 제시된 연구 라인이 더 추구할 가치가 있다고 강력히 믿습니다. 여기서는 이진 MIL 문제에 초점을 맞추었지만 다중 클래스 MIL이 더 흥미롭고 도전적입니다(Feng & Zhou, 2017). 또한, 일부 응용 프로그램에서는 반발 지점(Scott et al., 2005), 즉 bag이 항상 음수인 경우를 고려하거나 가방 내 인스턴스 간의 종속성을 가정하는 것이 가치가 있습니다(Zhou et al., 2009). 우리는 향후 연구를 위해 이러한 문제를 조사합니다.
Acknowledgements(감사의 말)
저자는 Rianne van den Berg에게 매우 감사합니다.
통찰력 있는 발언과 토론. Maximilian Ilse는 Nederlandse Organisatie voor Wetenschappelijk Onderzoek(Grant DLMedIa: 의료 이미지 분석을 위한 딥 러닝)의 지원을 받았습니다.
Jakub Tomczak은 Marie Skodowska-Curie Individual Fellowship(보조금 번호 702666, "의료 영상을 위한 딥 러닝 및 베이지안 추론") 내의 유럽 위원회에서 자금을 지원했습니다.
