용어 정리
앨리어싱(Aliasing) : 대각선이 지그재그 현상
스칼라(scalars) : 방향이 없이 크기만 갖고 있다. 결합,교환 법칙이 성립한다.
벡터(vectors) : 방향과 크기를 갖고 있다. 스칼라 값이 곱해 질 수 있다.
- 벡터끼리 더해질 수 있음
포인트(points) : point-point = vector / vector+point = point
Vector Space : scalars와 vectors 두개의 타입을 가지고 있음
Affine Space : scalars, vectors, points 세가지를 모두 포함한 공간
Line : Point에 vector를 더해주면 line 생성

교수님이 보라고 한것
1번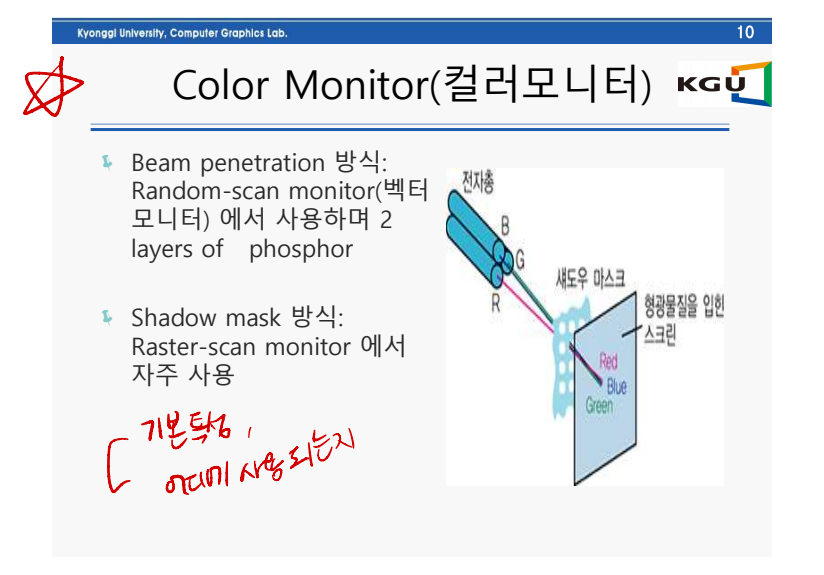
2번
벡터그래픽 장치와 레스터 그래픽 장치 차이점
- 화소 개념 없음(무한 해상도)
- 에일리어싱 없음
- 전차총의 움직임 (선을 꼭직점마다 연결해주는 과정)
- 프레임 버퍼 없음
- 디스플레이 리스트에 Drawing 명령어 집합을 써준다.
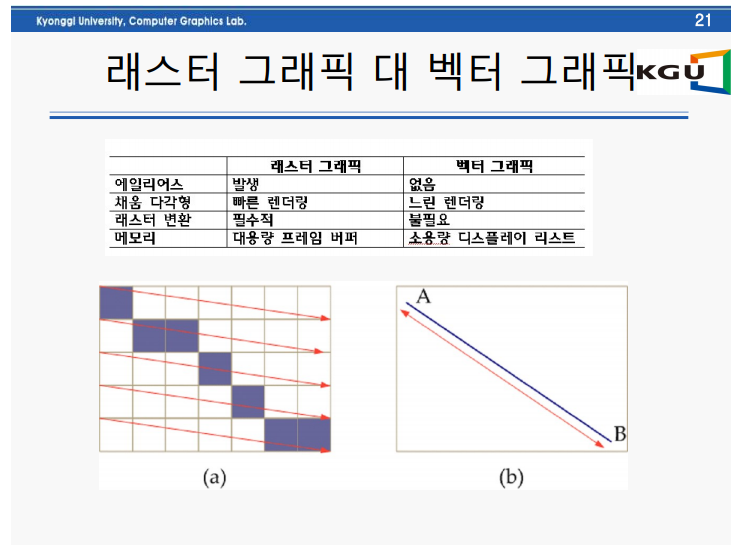
3번
opengl 함수별 의미 알아 두기(족보 참고)
4번
openGL 장점, 특성 알아두기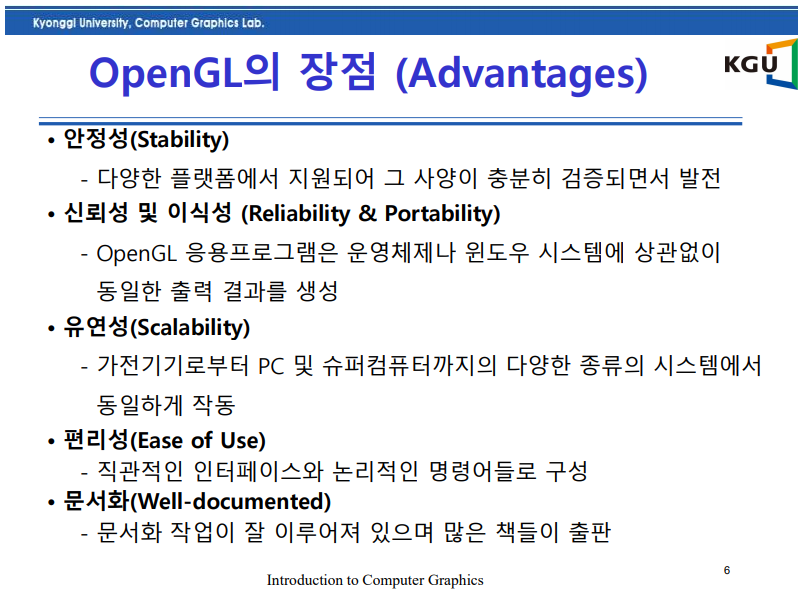
5번
벡터 구하기 연습하기(족보)
6번
동차 좌표계 써야하는 이유 :

7번
렌더링 과정이 어떻게 진행이 되고 최종결과가 어떻게 되는지(외울 필요x)
8번
DDA선 그리기(원리 알아두기)
9번
브레스넘 알고리즘 원리 알기
10번
Aliasing 원리 뭔지 알기
11번
RGB, CMY, HSV 컬러 모델의 차이점 알아놓기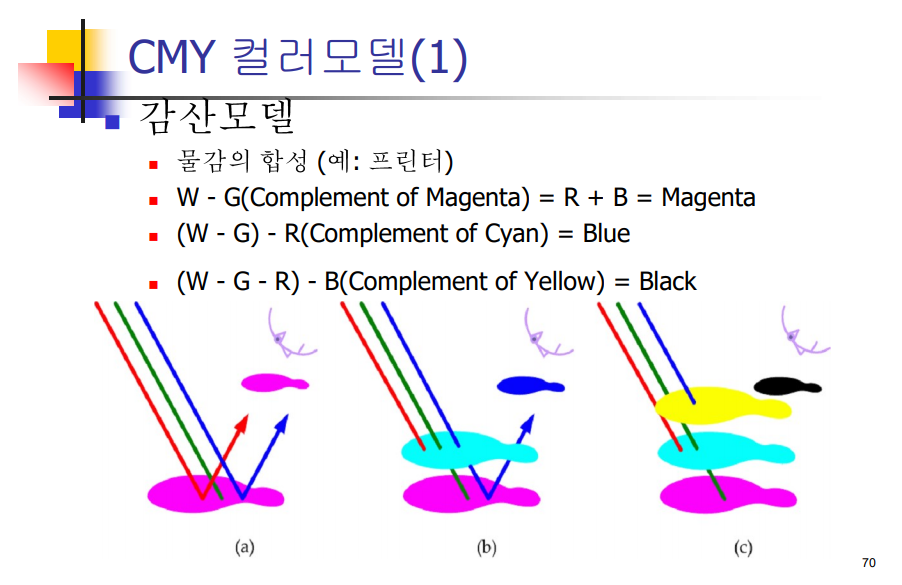
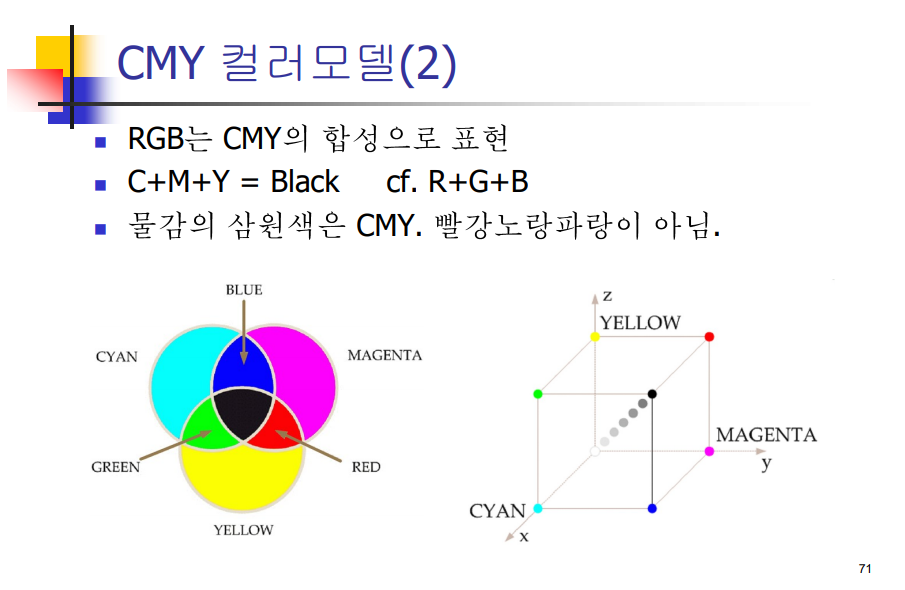

12번
임의의 점에 대한 신축하는 방법 알기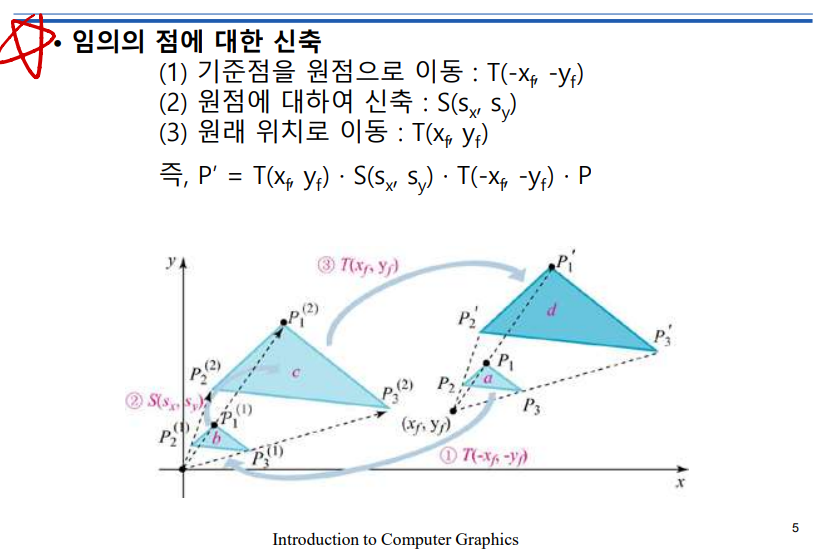
13번
동차 좌표계를 사용하는 이유
물체 이동, 신축, 변환하는데 덧셈 곱셈으로 연산을 하기 위해서 행렬의 사이즈가 일치해야 하지만 식이 성립이 안된다. 따라서 정형화된 행렬 크기를 이용해서 물체의 변환을 모두 곱셈의 연산으로 할 수 있도록(덧셈을 제외) 만들어 준다. 또한 여러가지 변환행렬을 하나의 행렬로 바꿔서 연산을 하면 연산량을 많이 줄 일 수 있는 장점도 있다.
14번
윈도우-뷰포트의 좌표변환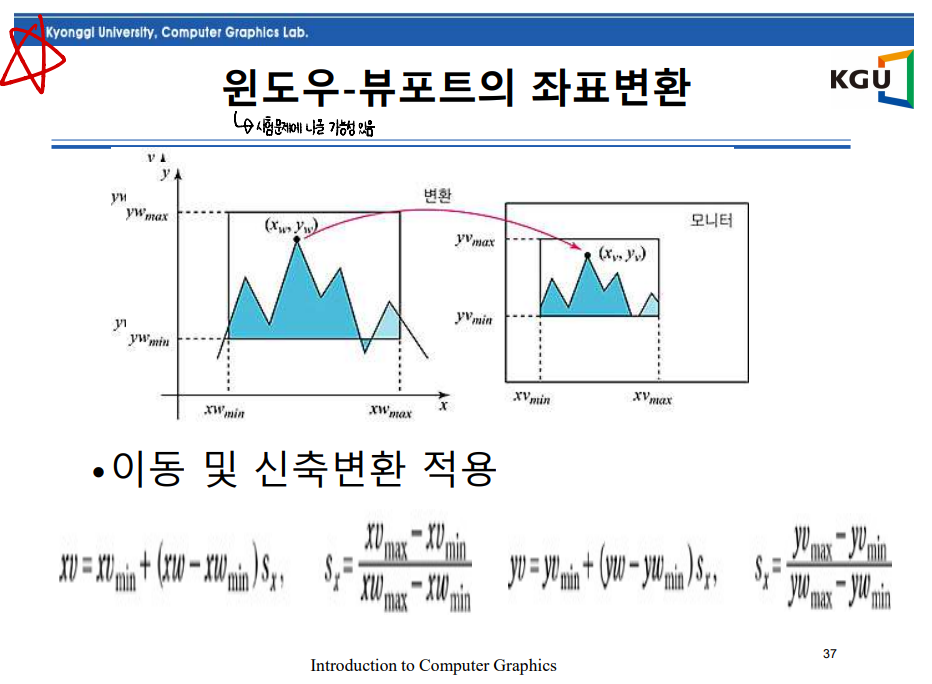
15번
코헨-서더랜드(Cohen-Sutherland) 알고리즘
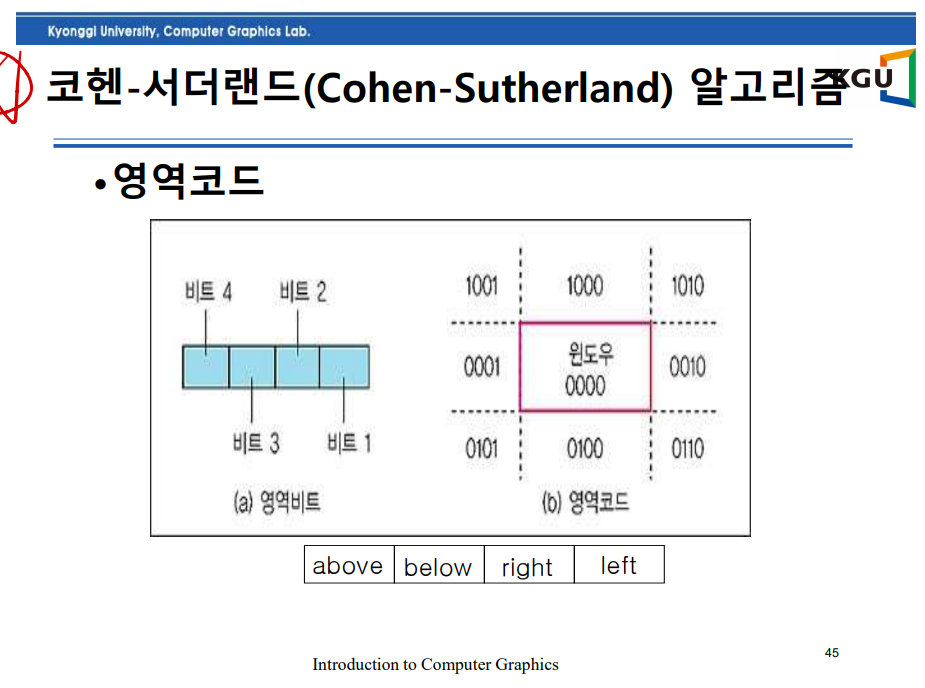
16번
UI의 주요 기법
Sample Mode // Request Mode 차이
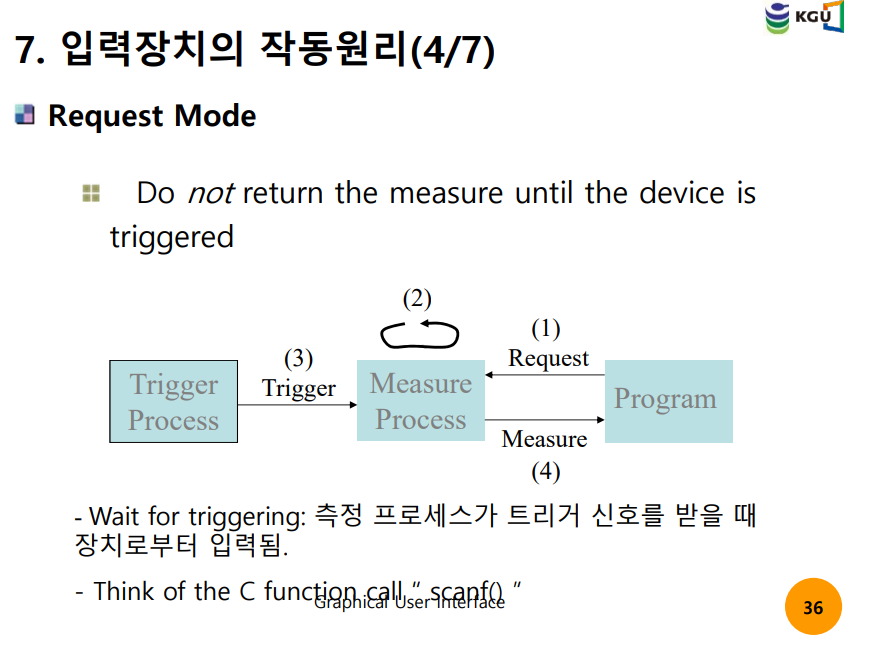
+대화식 입력기법 뭔지는 알고 있지
17번
2. 투영(Projection) 차이
투영(가시 변환) :3차원 객체를 2차원 출력장치에 맵핑하는 작업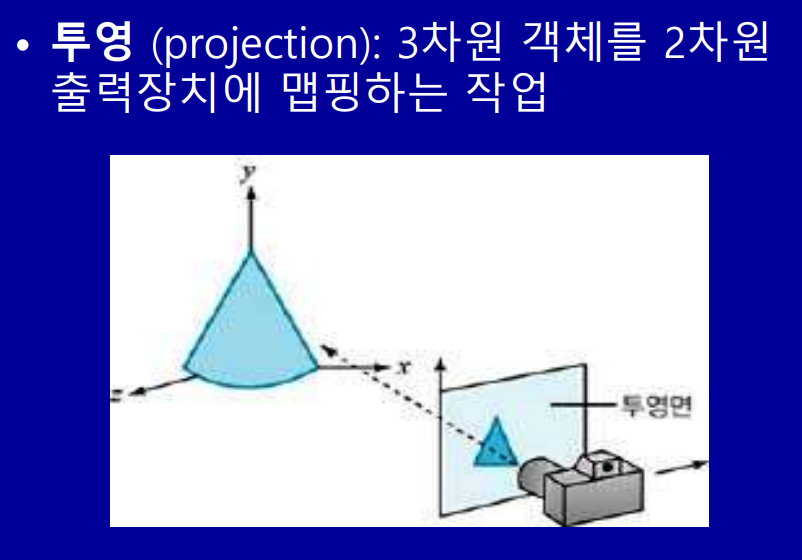
1) 관측자와 물체 간의 거리
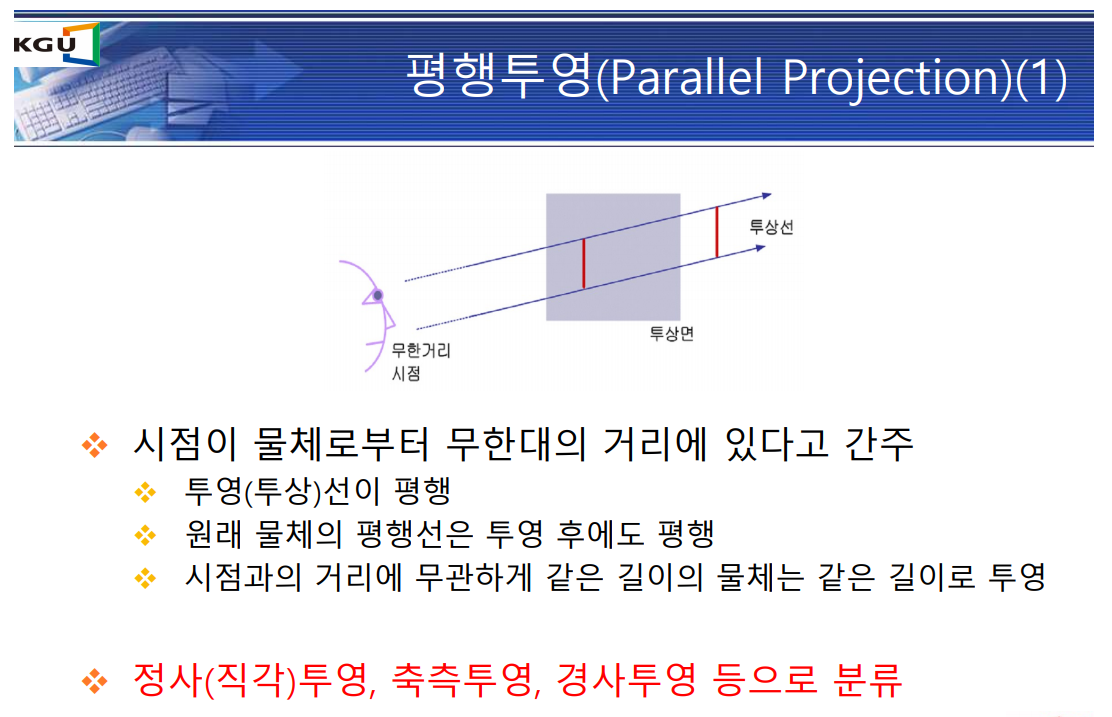
2) 장단점 비교
직각(정사) 투영

직교 투영의 장단점
- 장점: distance(거리)와 angle을 유지한다.
- 단점: 물체 전체를 관찰하기에는 어려움이 있다. 면이 복잡할 경우 -> 축측투영으로 해소할 수 있다(여러면을 볼 수 있음).
축측 투영


축측 투영 장단점
- 라인이 줄어들어서 보임. 그래도 scaling factors는 찾을 수 있음
- 라인은 유지되지만 앵글은 유지되지 않음
- 상자와 같은 물체의 세 가지 주요 면을 볼 수 있음
- 일부 착시 가능성이 있음(평행선이 갈라지는 것처럼 보입니다.)
- 멀리 있는 물체는 가까운 물체와 동일하게 크기가 조정되기 때문에 실제처럼 보이지 않음
- CAD 응용 프로그램에 사용됨
경사 투영
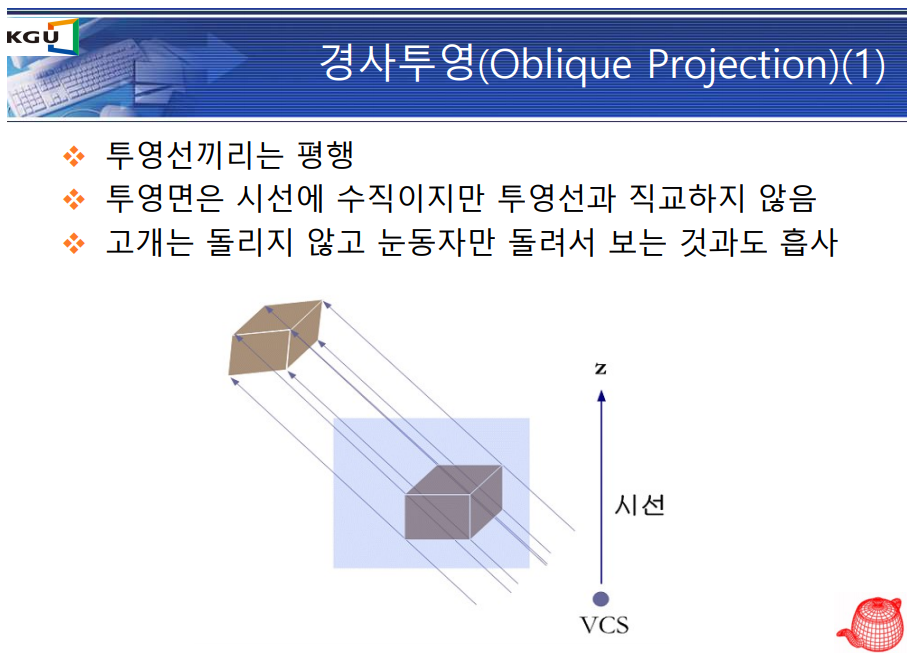

경사 투영 장단점
- 특정 face를 강조하기 위해 각도를 선택할 수 있음(건축: 평면 경사, 입면 경사)
- 투영 평면에 평행한 면의 각도는 유지되지만 주변 측면은 볼 수 있음.
- 물리적 세계에서는 단순한 카메라로 만들 수 없음(구현하기 어려움). 벨로우즈 카메라 또는 특수 렌즈(건축용)로 가능함
원근 투영
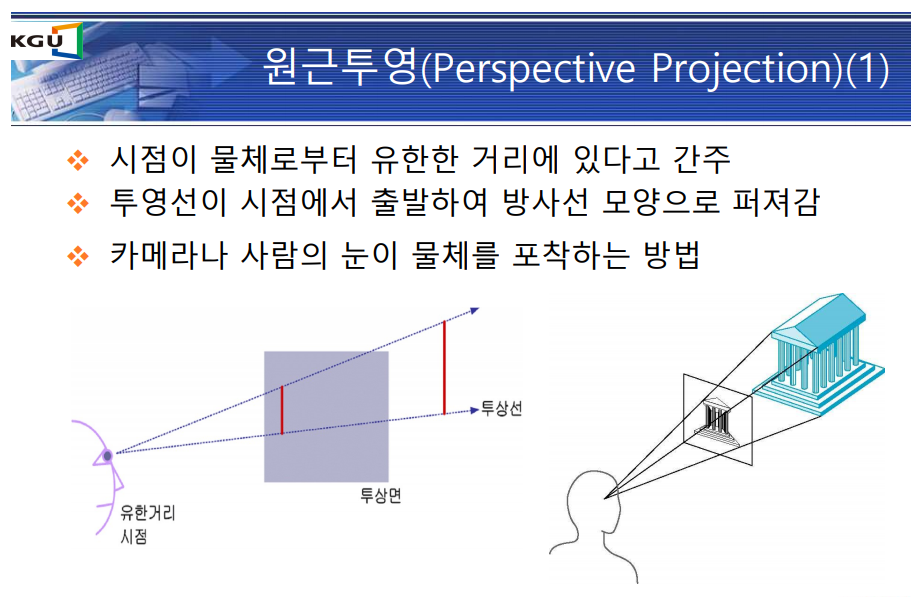


원근 투영 장단점
- 뷰어에서 멀리 떨어진 물체는 뷰어에 가까운 동일한 크기의 물체보다 작게 투영됨(축소) : 진짜 처럼 보임
- 선을 따라 동일한 거리는 동일한 거리로 투영되지 않음(비균일 단축) : projection됐을 때 실제 길이만큼 비례하여 줄어들지 않음
- 투영 평면과 평행한 평면에서만 angle은 유지됨
- 평행 투영보다 손으로 구성하기가 더 어려움(그러나 컴퓨터로 어렵지는 않음).
3) Projection Matrix 유도 과정
이거 모르겠음
그냥 뭔가 알아놓으면 좋을만한것
x축 회전
y축 회전
