abstract
MIL(Multiple Instance Learning)은 패턴 인식 커뮤니티에서 중요한 화두가 되었고, 이 문제에 대한 많은 해결책이 지금까지 제안되어 왔다. 이러한 사실에도 불구하고, 서로 다른 방법의 특성과 동작을 밝히는 비교 연구는 부족합니다. 이 작업에서는 분류 작업에 초점을 맞춘 분석을 제공합니다(즉, 회귀와 같은 다른 학습 작업은 생략). 연구를 수행하기 위해 세 가지 다른 제품군으로 그룹화된 14가지 방법을 구현했습니다. 잘 알려진 다양한 데이터베이스에서 접근 방식의 성능을 분석하고 특성을 강조하기 위해 합성 시나리오에서 동작을 연구합니다. 분석 결과 global bag-level 정보를 추출하는 방법이 전반적으로 확실히 우수한 성능을 보인다는 결론을 얻었다. 이러한 의미에서 분석을 통해 일부 유형의 방법이 다른 유형보다 더 성공적인 이유를 이해할 수 있으며 새로운 MIL 방법 설계에 대한 지침을 설정할 수 있습니다.
1. Introduction
표준 감독 학습 작업에서 각 feature 벡터에는 관련 클래스 레이블이 있는 feature 벡터의 훈련 세트를 기반으로 분류기를 학습합니다. MIL(Multiple Instance Learning) 작업에서 우리는 가방의 훈련 세트를 기반으로 분류기를 학습합니다. 여기서 각 가방에는 여러 feature 벡터(MIL 용어로 인스턴스라고 함)가 포함됩니다. 이 설정에서 각 백에는 연관된 레이블이 있지만 백을 준수하는 개별 인스턴스의 레이블을 알 수 없습니다. 또한 모든 인스턴스가 반드시 관련이 있는 것은 아닙니다. 즉, 해당 클래스에 대한 정보를 전달하지 않거나 다른 클래스의 bag과 더 관련되어 혼란스러운 정보를 제공하는 인스턴스가 하나의 bag 내부에 있을 수 있습니다.
많은 분야에서 다중 인스턴스 학습 설정을 사용하여 가장 자연스럽게 공식화되는 문제를 찾습니다. 약물 발견(약국), 텍스트 문서 분류(정보 검색), 이미지 분류(컴퓨터 비전), 화자 식별(신호 처리) 및 파산 예측(경제)의 경우입니다. 이 프레임워크(실제 예제에 대한 자세한 내용은 섹션 2 참조). 이로 인해 MIL 문제는 지난 몇 년 동안 많은 방법이 발표된 기계 학습 커뮤니티에서 중요한 주제가 되었습니다. 이러한 사실에도 불구하고 다양한 MIL 알고리즘 제품군의 성능을 비교하는 조사 또는 분석 연구가 부족합니다.
이 작업에서는 회귀와 같은 다른 학습 작업을 제외하고 다중 인스턴스 분류(MIC)에 중점을 둡니다. 우리는 철저한 실증적 비교와 함께 문헌의 방법에 대한 광범위한 검토를 제시합니다. 분석에서는 다중 인스턴스(MI) 데이터의 정보를 관리하는 방법에 따라 방법을 소형 패러다임의 작은 세트로 그룹화했습니다. 앞으로 보게 되겠지만, 모든 MIC 방법은 반드시 제안된 분류 체계 중 하나에 속해야 한다는 의미에서 우리의 특성화는 완전합니다. 또한 각 패러다임에 해당하는 방법들은 유사한 행동을 보이는 경향이 있어 실험 평가에서 패러다임을 쉽게 분석하고 비교할 수 있습니다. 제안된 분류법의 일부로서 우리는 처음으로 어휘 기반 패러다임을 특징지었습니다. 이 패러다임과 다른 패러다임의 주요 차이점은 어휘 기반 패러다임에서는 인스턴스가 여러 클래스로 분류되거나 구별되는 반면 다른 패러다임에서는 그러한 차별이 없다는 것입니다. 많은 저자 [1], [2], [3], [4], [5], [6], [7], [8], [9]는 어휘 기반 패러다임에 속하는 알고리즘을 제안했지만, 이러한 모든 접근 방식 간의 관계는 지금까지 확립되지 않았습니다. 이 작업에서 우리는 그들 모두가 Vocabulary 기반 family에 속한다는 것을 보여주고 이 family의 명확한 특성을 제공합니다.
우리는 Foulds와 Frank[10]의 최근 리뷰와 Lin Dong[11]의 석사 논문에서 수행된 비교 연구만 알고 있다. 불행하게도, 이 출판물에는 우리가 이 백서에서 보여주는 중요한 패러다임인 어휘 기반 기술 계열이 포함되어 있지 않습니다. [11]에서 Lin Dong은 많은 방법의 정량적 분석을 보여주지만 결정적인 결과를 얻지 못하고 Vocabulary-based paradigm에서 많은 중요한 알고리즘을 생략합니다.
최근 Foulds와 Frank[10]는 각각에 따르는 가정에 따라 MIC 방법을 분류했습니다. 이 작업에서 보여주듯이 [10]에서 제안된 방법의 많은 범주는 우리 작업에서 특성화된 어휘 기반 방법에 속합니다. 우리는 Foulds와 Frank가 각 방법이 따르는 가정에 따라 방법을 분류한다는 점에서 보완적인 분석을 제시하고, 이 분류는 각 방법에서 추출한 정보의 유형(인스턴스 수준 또는 백 수준 정보)과 표현 방법(암시적 또는 명시적으로)에 따라 수행합니다. 이런 의미에서 우리의 분석은 [10]과 충돌하지 않습니다. 또한 제안된 패러다임에 대한 경험적 평가를 제공하고 [10]에서 수행되지 않은 동작을 분석합니다.
요약하면, 이 작업은 MIC 방법의 새로운 분석 및 분류와 철저한 비교 분석에 기여합니다. 전체적으로 우리가 구현한 14개의 MIC 알고리즘을 분석하고 4개의 서로 다른 지식 분야의 8개 데이터베이스와 제어된 조건에서 방법의 동작을 연구한 합성 데이터베이스를 사용합니다. 이 작업의 예비 버전은 [12]에 나타났습니다.
나머지 논문은 다음과 같이 구성된다. 섹션 2에서는 실제 사례를 통해 다중 인스턴스 분류 사용의 필요성을 자세히 설명합니다. 섹션 3에서는 MIC 문제와 제안된 분류법을 설명합니다. 섹션 4, 5, 6에서는 분류법의 주요 패러다임인 인스턴스 공간 패러다임, 백 공간 패러다임 및 임베디드 공간 패러다임을 설명합니다. 후자의 패러다임은 섹션 7에서 자세히 설명하는 어휘 기반 방법 계열을 포함합니다.
9장에서는 서로 다른 패러다임에 대한 비교 분석을 제공하고 10장에서 결론을 제시합니다.
2. Examples of multiple-instance classification problems
여기에서 MI 표현이 필요한 두 가지 실제 문제, 즉 분류할 객체가 단일 특징 벡터로 표현되는 전통적인 학습 문제와 달리 분류할 객체가 백(여러 특징 벡터 포함)으로 설명되는 두 가지 실제 문제를 설명합니다.
첫 번째는 약물 활성 예측 문제이다[13]. 이 문제에서 분류할 대상은 화학 분자입니다. 분자가 주어지면 시스템은 그것이 좋은 약인지 아닌지를 결정해야 합니다. 좋은 약물은 훨씬 더 큰 분자에 존재하는 일종의 공동인 표적 "결합 부위"에 강하게 결합할 수 있다는 사실이 특징입니다[13]. 어려움은 하나의 분자가 여러 개의 3차원 형태(구조라고 함)를 채택할 수 있고 그 중 하나 또는 몇 개만이 표적 결합 부위와 잘 결합한다는 사실에서 비롯됩니다. 이러한 유형의 문제에서 전체 분자는 백 X = {x1,..., xN }로 설명되며, 이는 N개의 가능한 형태에 대한 설명을 수집하는 집합입니다. 여기서 xi(i=1,...,N)는 i번째 형태를 설명하는 특징 벡터이고 구조 N의 수는 분자마다 다를 수 있습니다.
MIC가 중요해지는 실제 문제의 또 다른 예는 이미지 분류입니다. 여기에서 주어진 이미지가 시각적 콘텐츠에 따라 대상 클래스에 속하는지 여부를 결정해야 합니다. 예를 들어 대상 클래스는 "해변"일 수 있으며 이 경우 포지티브 이미지는 해변을 표시하는 이미지이고 네거티브 이미지는 다른 유형의 시각적 콘텐츠를 표시하는 이미지입니다.

그림 6은 이 이미지 분류 작업의 예를 보여주며 나중에 빨간색 원의 의미를 설명합니다. 이 그림에서 맨 윗줄의 이미지는 양수이고 맨 아래 줄의 이미지는 음수입니다(그 중 하나는 해변이 없는 바다를 표시하고 다른 이미지는 사막을 표시함). 이 그림에는 두 개의 부정적인 이미지만 표시되어 있지만 시골, 도시, 자동차, 사무실 등과 같은 다른 유형의 콘텐츠를 포함하는 다른 많은 부정적인 이미지가 있습니다. 그림 6의 맨 윗줄에 있는 긍정적인 이미지를 보면 , 대상 클래스와 관련된 이미지 영역(모래와 바다에 속하는 영역)이 있는 반면 특별히 관련되지 않은 영역(예: 하늘, 산, 나무)이 있음을 알 수 있습니다. , 등.).
해변 이미지를 얻으려면 바다와 모래가 모두 필요하지만 나머지 지역은 필요하지 않습니다. 이미지를 분류하기 위해 일반적인 절차는 먼저 이미지에서 영역 모음을 추출하고 각 영역에 대해 시각적 설명자(descriptor)를 얻는 것입니다. 이 시각적 설명자(descriptor)는 영역을 설명하는 feature vector입니다. 결과적으로 이미지는 백 X = {x1,..., xN }으로 기술되며, 여기서 N은 추출된 영역의 수이고 xi는 이미지의 i번째 영역을 설명하는 특징 벡터(인스턴스라고 함)입니다. 그림 6에서 우리는 다른 지역에서 시각적 설명자 추출을 상징하기 위해 빨간색 원을 사용합니다. 추출된 영역의 수는 관심 영역을 식별하기 위한 특정 알고리즘에 따라 다르며 이미지마다 다를 수 있습니다.
이들은 백 표현을 사용하여 문제를 MIC로 설정하는 것이 필요한 실제 문제의 두 가지 예일 뿐입니다. 이 두 가지 문제 외에도 정보 검색, 오디오 처리, 경제 예측 등의 분류 작업을 포함하여 서론에서 언급한 바와 같이 이러한 유형의 공식화를 필요로 하는 다른 많은 문제 영역이 있습니다.
이 백서의 나머지 부분에서는 MIC 문제를 해결하기 위한 다양한 접근 방식을 연구합니다.
3. Basic concepts and overview of paradigms
백은 집합 X = {x1,..., xN }입니다. 여기서 요소 xi는 MIC 용어에서 인스턴스라고 하는 feature 벡터이고 카디널리티 N은 백에 따라 다를 수 있습니다. 모든 인스턴스 xi는 인스턴스 공간이라고 하는 d차원 feature space xi ∈ R^d에 있습니다.
MIC 문제의 목적은 training 시간에 보이지 않는 가방의 클래스 레이블을 예측하는 데 사용할 수 있는 모델을 학습하는 것입니다. 이 작업에서는 가방 X가 양수 또는 음수가 될 수 있는 이진 분류 문제만 고려합니다.
우리의 목표는 X가 양수일 가능성을 제공하는 분류 함수 F (X) ∈ [0, 1]을 추정하는 것입니다. 이러한 기능을 학습하기 위해 M개의 백과 해당 레이블이 있는 훈련 세트, T = {(X1, y1),...,(XM , yM)}가 주어집니다. 여기서 yi ∈ {0, 1}은 Xi의 레이블입니다(yi = 0 if Xi는 음수이고 양수이면 yi = 1입니다.
백 수준 분류 함수 F(X) 외에도 많은 방법이 인스턴스 x_i에서 직접 작동하는 인스턴스 수준 분류 함수 f(x_i)를 학습하려고 합니다. 이 작업 전반에 걸쳐 우리는 가방 X와 가방 수준 분류자 F를 참조하기 위해 대문자를 사용하고 인스턴스 x와 인스턴스 수준 분류기 f를 참조하기 위해 소문자를 사용할 것입니다.
3.1. Overview of proposed taxonomy
3.1. 제안된 분류 개요
이 연구에서는 MI 데이터에 존재하는 정보가 어떻게 활용되는지에 따라 MIC 방법을 분류합니다(그림 4 참조).
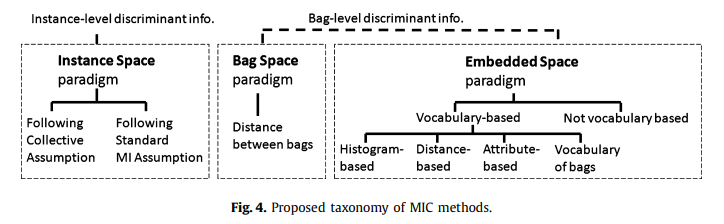
IS(Instance-Space) 패러다임에서 식별 정보는 인스턴스 수준에 있는 것으로 간주됩니다. 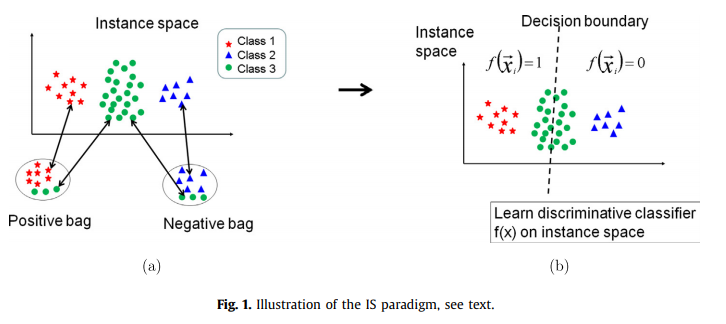
따라서 차별적 학습 프로세스는 다음 수준에서 발생합니다 : 식별 인스턴스 수준 분류기 f(x)는 양성 백의 인스턴스와 음성 백의 인스턴스를 분리하도록 훈련됩니다(그림 1 참조). 이를 기반으로 새로운 백 X가 주어지면 인스턴스 레벨 점수 f(x), x ∈ X를 단순히 집계하여 백 레벨 분류기 F(X)를 얻습니다.
이러한 유형의 패러다임은 학습 프로세스가 전체 가방의 더 많은 글로벌 특성을 보지 않고 개별 인스턴스의 특성을 고려한다는 의미에서 로컬 인스턴스 수준 정보를 기반으로 합니다.
Bag-Space(BS) 패러다임에서 식별 정보는 bag-level에 있는 것으로 간주됩니다. 이 패러다임에서 각 가방 X는 전체 개체로 취급되며 학습 프로세스는 전체 가방을 구별합니다. 결과적으로 X의 클래스에 대한 차별적 결정을 내리기 위해 전체 백 X의 정보를 사용하는 차별적 백 수준 분류기 F(X)를 얻습니다.
이러한 유형의 패러다임은 로컬 인스턴스 수준의 결정을 집계하는 대신 전체 가방을 살펴봄으로써 차별적인 결정을 내리기 때문에 글로벌, 가방 수준 정보를 기반으로 합니다.
백 공간이 비벡터 공간이라는 사실을 감안할 때 BS 방법은 비벡터 학습 기법을 사용합니다. 우리가 아는 한, 존재하는 모든 비벡터 기술은 임의의 두 비벡터 엔티티 X와 Y를 비교하는 방법을 제공하는 거리 함수 D(X, Y)의 정의를 통해 작동합니다.(이러한 엔터티가 우리 문제의 가방인 경우).
이 거리 함수가 정의되면 K-NN(K-Nearest Neighbor)과 같은 표준 거리 기반 분류기 또는 SVM과 같은 커널 기반 분류기에서 유사하게 사용할 수 있습니다.
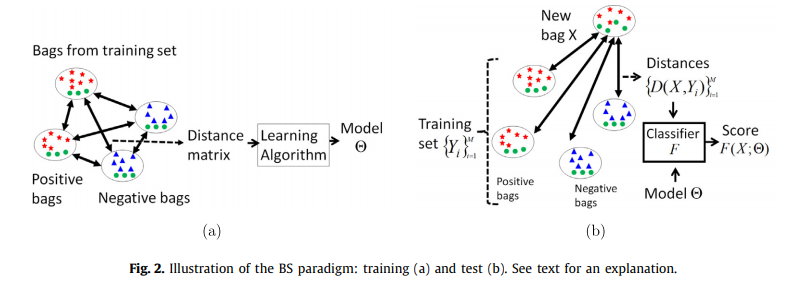
그림 2는 이 패러다임 아래의 아이디어를 보여줍니다. 그림 2에서 "거리"라는 용어를 사용하지만 BS 패러다임에는 SVM 기반 방법의 커널 기반 비교 K(X, Y)와 같은 백 사이의 다른 유형의 쌍별 비교를 사용하는 방법도 포함됩니다.
백 레벨 분류기와 관련하여 분류기가 학습된 매개변수 Θ를 사용한다는 사실을 표현하기 위해 그림 2(b)의 표기법 F(X;Θ)를 사용합니다(그림 2(a) 참조). . 그러나 논문에서는 표기법 F(X)를 사용하고 단순화를 위해 인수 Θ를 생략합니다.
ES(Embedded-Space) 패러다임에서 각 가방 X는 전체 가방 X에 대한 관련 정보를 요약하는 단일 기능 벡터에 매핑됩니다.
결과적으로 원래의 백 공간은 판별 분류기가 학습되는 벡터 내장 공간에 매핑됩니다. 이것은 원래의 MIC 문제를 표준 감독 학습 문제로 효과적으로 변환합니다. 각 feature 벡터에는 관련 레이블이 있고 AdaBoost, Neural Networks 또는 SVM과 같은 표준 분류기가 적용될 수 있습니다. 그림 3은 이 패러다임 아래의 아이디어를 보여줍니다.
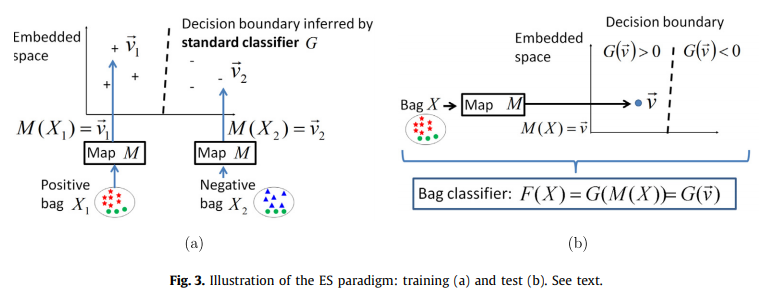
ES 패러다임은 백 X가 전체 백에 대한 관련 정보를 요약하는 특징 벡터 v로 표현된다는 점에서 글로벌 백 level 정보를 기반으로 합니다. 이 feature 벡터가 주어지면 백 레벨 분류기 F(X)는 F(X) = G(v)로 표현될 수 있습니다. 여기서 G는 전체 백을 요약하는 벡터 v를 기반으로 결정을 내리는 판별 분류기입니다.
이러한 의미에서 ES와 BS 패러다임은 글로벌 백 레벨 정보를 이용합니다. 그러나 두 패러다임의 차이점은 이 백 레벨 정보가 추출되는 방식에 있습니다. BS 패러다임에서 이것은 거리 또는 커널 함수의 정의를 통해 암시적으로 수행됩니다.
대조적으로, ES 패러다임에서는 관련 정보가 단일 벡터 v로 표현되는 방법을 정의하는 매핑 함수의 정의를 통해 전체 가방에서 정보 추출이 명시적으로 수행됩니다.
따라서 instance-level 정보(IS paradigm) 또는 global, bag-level 정보에 초점을 맞추는지 여부에 따라 방법을 분류하고, 마지막 경우 암시적으로(BS paradigm) 또는 명시적으로(ES paradigm) 관련 정보를 추출하는지 여부에 따라 분류합니다. 이 외에도 각 패러다임에 대한 특징적인 계산 비용도 있습니다.
3.2. Completeness of the proposed categorization
3.2. 제안된 분류의 완전성
제시된 분류는 문헌의 MIC 방법이 주어지면 반드시 IS, BS 또는 ES의 세 가지 계열 중 하나에 속해야 한다는 점에서 완전합니다. MIC 방법이 모든 x ∈ X에 대한 인스턴스 수준 분류 f(x) ∈ [0, 1]의 집합으로 백 수준 분류 F(X) ∈ [0, 1]을 얻으면 IS 패러다임에 속합니다. 그렇지 않으면 방법은 BS 또는 ES 패러다임에 속합니다. 후자의 경우 가방 X가 특징 벡터 v에 매핑된 다음 표준 분류기로 분류되면 ES 패러다임에 속합니다. 그렇지 않고 그러한 매핑이 적용되지 않고 Bag이 전체적으로 분류되는 경우 BS 방식이 있습니다.
모든 범주화에서 우리는 항상 두 범주의 경계에 가까운 방법을 찾을 것입니다. 예를 들어 우리 분류법에서 이것은 BARTMIP 방법에서 발생합니다(섹션 7.6 참조).
이것은 각 가방 X가 벡터 v에 명시적으로 매핑되는 ES 방법입니다.
그러나 매핑을 수행하기 위해 가방 수준 거리 함수 D(X, Y)의 정의를 통해 가방 X를 훈련 세트의 다른 가방 Y와 비교합니다.
이런 의미에서 이 방법은 ES와 BS 범주 사이의 경계에 가깝습니다.
3.3. Illustrative examples
3.3. 예시적인 예
나머지 작업에서는 두 가지 예시적인 합성 예제를 사용할 것입니다.
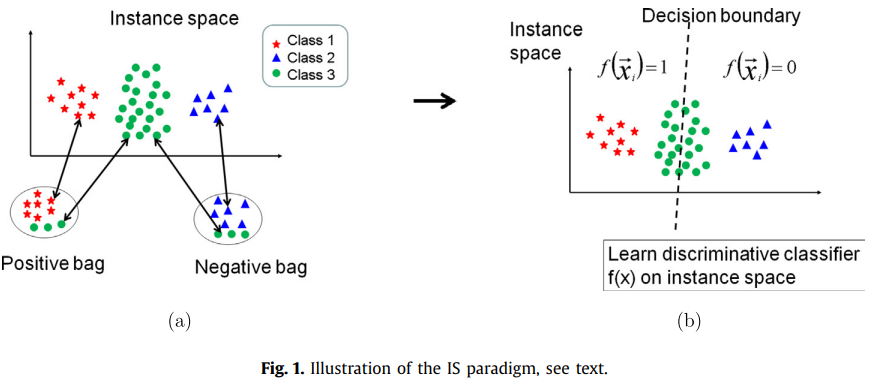
첫 번째는 그림 1에 나와 있으며 인스턴스 수준 정보가 MIC 문제를 해결하기에 충분한 경우를 보여줍니다. 이는 포지티브 백에만 나타나는 인스턴스의 특정 클래스가 있을 때 발생하므로 이러한 클래스의 (인스턴스 수준) 모델을 학습하는 것으로 충분합니다. 특히 그림 1의 예에서 인스턴스 클래스 1은 포지티브 백에만 나타납니다. 따라서 인스턴스 x가 클래스 1에 속한다는 확신을 제공하는 인스턴스 수준 분류기 f(x) ∈ [0, 1]을 학습하는 것으로 충분합니다.
f(x)가 학습되면 가방 수준 분류기 F(X)는 인스턴스 수준 점수에 대해 최대값을 취함으로써 간단하게 얻을 수 있습니다: F(X) = max x∈X f(x).
이런 식으로 가방 X는 인스턴스 x ∈ X 중 하나라도 클래스 1에 속하면 양성으로 분류되고 그렇지 않으면 음성으로 분류됩니다.
이러한 접근 방식을 사용함으로써 학습은 인스턴스 수준에서만 수행됩니다. 즉, 인스턴스 수준 분류기 f(x)에서 사용되는 클래스 1의 인스턴스 모델을 얻기 위해 학습이 수행됩니다. 그러나 백 level에서는 분류기 F(X)가 인스턴스 수준 점수의 집계로 얻어지기 때문에 학습이 없습니다. 이러한 유형의 접근 방식은 섹션 4에서 특성화되는 IS 패러다임의 일부를 형성하며 그림 1과 같은 MIC 문제에 적용됩니다. 여기서는 양성 백에만 나타나는 인스턴스 클래스가 적어도 하나 있습니다.(또는 반대 방향으로, 네거티브 백에만 나타나는 인스턴스 클래스가 하나 이상 있습니다).
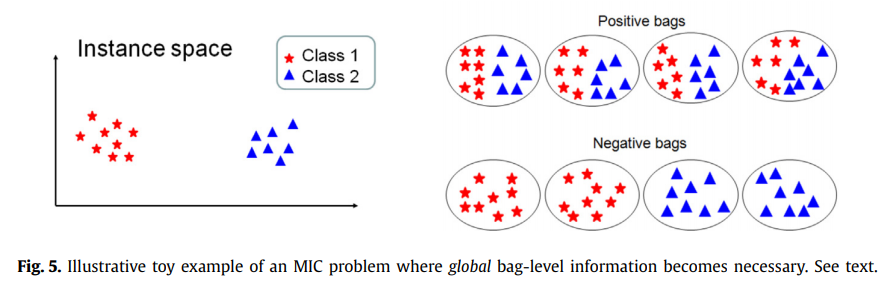
그림 5는 이것이 발생하지 않는 또 다른 합성 MIC 문제를 보여줍니다. 여기에는 두 가지 인스턴스 클래스가 있으며 둘 다 포지티브 백과 네거티브 백에 나타납니다. 따라서 긍정적인 가방이나 부정적인 가방에만 나타나는 단일 클래스의 사례는 없습니다. 이러한 유형의 문제에서는 인스턴스 수준에서만 학습을 수행할 수 없습니다.
예를 들어, f(x)를 얻기 위해 클래스 1의 인스턴스 수준 모델을 학습하는 경우 양성 및 음성 백 모두 클래스 1의 인스턴스를 포함한다는 것을 알기 때문에 개별 점수 f(x)만을 기준으로 분류 F(X)를 추론할 수 없습니다. 클래스 2의 인스턴스 수준 모델을 학습하는 경우에도 마찬가지입니다.
그림 5의 백 구성을 보면 긍정적인 백이 클래스 1과 클래스 2의 인스턴스를 모두 포함하는 특징이 있음을 알 수 있습니다.
대조적으로, 네거티브 백은 클래스 1의 인스턴스 또는 클래스 2의 인스턴스를 포함하지만 동시에 둘 다 포함하지는 않는다는 특징이 있습니다. 따라서 인스턴스 클래스의 (인스턴스 수준) 모델을 학습하는 것만으로는 충분하지 않고 전체 가방의 구성에 대한 가방 수준 모델을 학습해야 합니다. 보시다시피, 이 백 레벨 정보는 BS 또는 ES 방법을 사용하면 학습할 수 있습니다. 실제로 우리는 그림 1과 그림 5의 문제 모두에서 BS와 ES가 모두 성공하는 반면 IS 방법은 첫 번째 유형의 문제에서만 성공한다는 것을 알 수 있습니다.

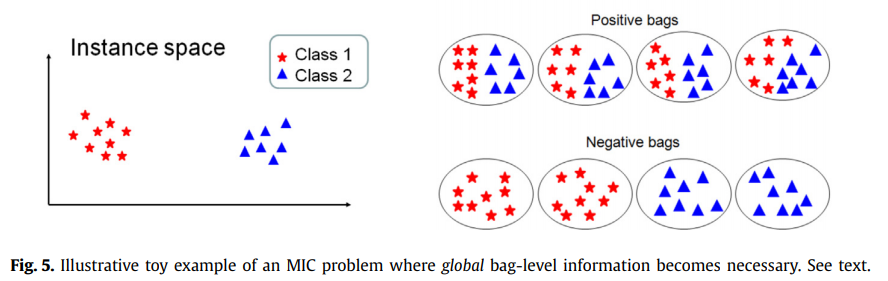
그림 6은 그림 5와 유사한 실제 MIC 문제를 보여줍니다.
문제는 이미지를 해변(상단 행 이미지)과 해변이 아닌 이미지(하단 행 이미지)로 분류하는 것과 관련이 있습니다. 여기에서 각 이미지는 인스턴스 백으로 설명되며 여기서 i번째 인스턴스 x_i는 이미지의 i번째 로컬 영역을 설명합니다. 이 아이디어는 각각 하나의 지역에 해당하는 빨간색 원을 사용하여 이미지에 기호화됩니다. 이 유형의 MIC 문제에서 각 백에는 이미지를 따르는 영역에 따라 여러 클래스의 인스턴스가 포함됩니다. 이미지가 beach 클래스에 속하려면 sand 클래스와 sea 클래스의 인스턴스가 동시에 발생해야 합니다. 그러나 이미지에서 이러한 클래스 중 하나만 발생하면 해당 클래스는 해변이 아닙니다. 이러한 유형의 MI 데이터는 이미지 분류 작업뿐만 아니라 MIC 문제에서도 자주 발생합니다. 이 외에도 분류에 대한 글로벌 백 수준 접근 방식이 근본적인 몇 가지 다른 예에 대해서도 논의할 것입니다.
3.4. Related work
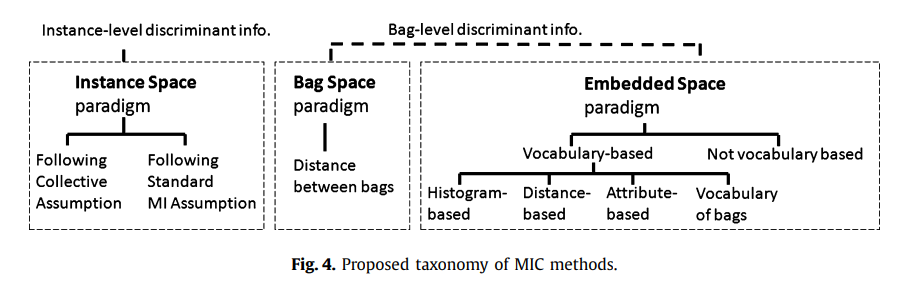
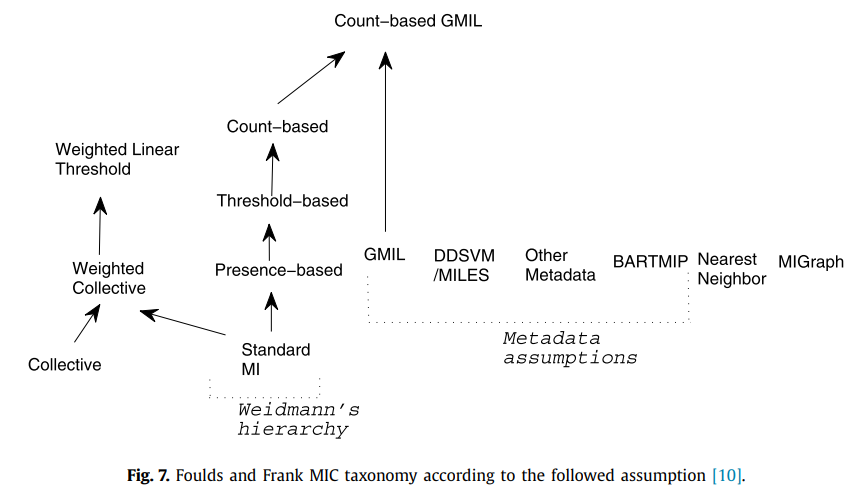
그림 7에서는 Foulds와 Frank[10]에서 제안한 범주의 계층 구조를 보여줍니다. 그림 4, 그림 7을 비교하면 [10]이 방법을 더 많은 패러다임으로 나누고 그 중 일부는 나머지와 분리되어 있음을 알 수 있습니다. 우리가 보게 되겠지만, 그림 7에서 분리된 패러다임의 대부분은 실제로 우리의 검토에서 처음으로 특성화되고 광범위하게 분석된 어휘 기반 패밀리의 일부입니다.
Foulds와 Frank는 서로 다른 기본 기준을 사용하여 분류법을 얻습니다. 그들의 경우, 가방 라벨과 인스턴스 사이의 관계에 대해 각 방법이 사용하는 가정에 주의를 기울입니다. 일부 가정은 각 방법의 작성자가 명시적으로 명시했고 일부는 그렇지 않았으므로 알고리즘을 통해서만 추측할 수 있습니다. 우리의 경우 판별 정보가 추출되는 수준과 표현 방법을 기준으로 사용합니다. 두 기준은 충돌하지 않으며 서로 다른 MIC 솔루션을 더 깊이 이해하는 데 도움이 됩니다. 또한 두 분류법의 목표가 반드시 동일하지는 않습니다. 우리의 경우 제안된 분류법에는 두 가지 목표가 있습니다.:
첫째, 기존 접근법에 대한 명확한 그림을 제공하고, 둘째, 그들이 속한 패러다임에 따라 방법을 비교할 수 있는 방식으로 방법에 대한 실험적 분석을 허용합니다.
이 마지막 목표는 비교 분석을 제공하지 않기 때문에 Foulds와 Frank가 반드시 추구하는 것은 아닙니다.
이제 IS 패러다임(섹션 4), BS 패러다임(섹션 5) 및 ES 패러다임(섹션 6)에 대해 자세히 설명합니다.
4. Instance-space paradigm
섹션 3에서 설명한 것처럼 IS 패러다임에서 아이디어는 훈련 데이터에서 인스턴스 기반 분류자 f(x) ∈ [0, 1]을 추론하는 것입니다. 이 분류기를 기반으로 가방 수준 분류 F(X) ∈ [0, 1]은 인스턴스 수준 응답의 집계로 구성됩니다.

여기서 ∘는 각 MIC 알고리즘에 특정한 집계 연산자를 나타내며(공통 연산자에 대한 검토는 아래 참조) Z는 Z=N(즉, 점수를 인스턴스 수로 나누기) 또는 정규화가 없는 경우 Z=1과 같은 선택적 정규화 계수를 나타냅니다.
이 범주에 속하는 방법은 레이블이 지정된 인스턴스의 교육 세트에 액세스하지 않고 인스턴스 수준 분류자 f(x)를 추론하는 방법에 대한 문제를 해결해야 합니다. 이 문제를 해결하려면 훈련 세트에 있는 가방의 레이블과 이 가방에 포함된 인스턴스의 레이블 간의 관계에 대해 몇 가지 가정을 해야 합니다. 이러한 의미에서 IS 방법의 두 가지 하위 범주는 문헌에서 명확하게 나타납니다. 표준 MI(SMI) 가정을 따르는 항목과 집합적 가정을 따르는 항목입니다.
4.1. IS methods following the SMI assumption
4.1. SMI 가정을 따르는 IS 방법
SMI 가정은 모든 포지티브 백에 적어도 하나의 포지티브 인스턴스(즉, 일부 대상 포지티브 클래스에 속하는 인스턴스)가 포함되는 반면 모든 네거티브 백에는 모든 인스턴스가 네거티브라고 명시합니다. 이것은 [13]의 약물 발견의 전통적인 문제와 같은 많은 MIC 문제에서 사용되는 비대칭 가정입니다. 이 가정은 인스턴스 중 하나에 백을 긍정적으로 만드는 몇 가지 바람직한 속성이 있다는 것입니다. 따라서 이 가정에 따른 방법들은 백을 긍정적으로 만드는 인스턴스의 유형을 식별하려고 합니다.
이 범주의 전통적인 방법 중 하나는 APR(Axis-Parallel Rectangle)입니다[13]. 이 방법에서 목표는 다음과 같이 정의된 인스턴스 수준 분류자 f(x; R)을 추정하는 것입니다.
여기서 R은 인스턴스 공간에서 Axis-Parallel Rectangle을 설명합니다. 매개변수 R은 R에 적어도 하나의 인스턴스를 포함하는 트레이닝 셋의 포지티브 백의 수와 동시에 R에 어떤 인스턴스도 포함하지 않는 네거티브 백의 수를 최대화하여 최적화됩니다. 이를 바탕으로 bag-level 분류기는 max 규칙을 사용하여 표현할 수 있습니다.
즉, 인스턴스 x ∈ X 중 적어도 하나가 양수이면 X는 양수로 간주됩니다. 최대 규칙은 다른 IS 방법에서 사용되는 가능한 집계(aggregation) 규칙 중 하나입니다. 특히 max 규칙은 DD[15], EM-DD[16], MI-SVM[17] 등에서도 사용된다. 바이너리 인스턴스 수준 분류자 f(x) ∈ {0, 1}이 있는 경우 논리 또는 집계 규칙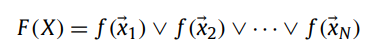
는 식(3)의 최대 집계 규칙과 동일합니다.
그러나 실제 값 분류기 f(x)가 있는 경우 최대 규칙은 일부 응용 프로그램에 도움이 될 수 있는 실제 값 백 수준 점수 F(X)를 얻을 수 있도록 허용합니다.
APR과 유사한 알고리즘은 DD(Diverse Density)[15]를 기반으로 하는 알고리즘입니다. 이 알고리즘에서 인스턴스 수준 분류자는 각 포지티브 백의 적어도 하나의 인스턴스에 가깝고 네거티브 백의 모든 인스턴스에서 멀리 떨어진 인스턴스 공간의 해당 지점에 대해 높은 DD 측정을 최대화합니다. [18]을 참조하고 [19]에서 이 알고리즘을 APR과 비교하는 추가 정보를 제공합니다.
MI-SVM 방법[17]에서 저자는 IS 분류기 f(x;Θ)를 제안하며, 여기서 Θ는 SVM에서 학습한 매개변수입니다. SVM을 추정하기 위해 반복적인 EM과 같은 접근 방식을 제안합니다. EM-DD(Expectation-Maximization Diverse Density) 알고리즘[16]에서 저자는 유사한 반복 접근 방식을 제안하여 이 경우 DD 측정을 최대화합니다. [19]에서는 IS 패러다임의 관점에서 이러한 알고리즘에 대한 자세한 내용을 제공합니다.
[20]에서 Bunescu와 Mooney는 역시 SVM을 기반으로 하는 SMIL(Sparse MIL) 알고리즘을 제안합니다. 인스턴스 수준 분류자 f(x;Θ)는 다음과 같이 정의된 양성 인스턴스 T = T + ∪ T −의 트레이닝 세트를 사용하여 학습됩니다.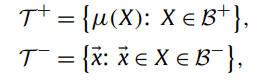
여기서 T+ 및 T-는 양수로 간주되는 인스턴스 집합과 음수로 간주되는 인스턴스 중 하나입니다.
μ(X)는 X 내부 인스턴스의 평균을 나타내며 B+ 및 B-는 각각 포지티브 및 네거티브 백 세트입니다.
이 훈련 세트가 주어지면 SMIL의 아이디어는 T+에서 양성 인스턴스의 분류에 대해 완화된 제약 조건으로 SVM 분류기를 학습하는 것입니다. 목표는 SVM이 포지티브 백의 모든 인스턴스에 대해 포지티브 값을 제공하도록 강제하지 않도록 하는 것입니다. 단, 인스턴스 중 적어도 하나에만 해당됩니다. 이를 위해 알고리즘은 다음 제약 조건에 따라 표준 SVM 목적 함수(자세한 내용은 [20] 참조)를 최소화하여 SVM 함수 f(x;Θ)의 매개변수 Θ를 추정합니다.
첫 번째 제약 조건 세트(1)는 SVM 함수가 음수 인스턴스에 적용될 때 음수 값을 제공하도록 강제합니다(여유 변수 ξ−를 통해 어느 정도의 오분류 허용).
두 번째 제약 조건 세트(2)는 긍정적인 인스턴스에 대해 보다 완화된 조건을 제공합니다. 이 조건은 μ(X)가 추출되는 백 X의 크기에 따라 달라집니다. X가 하나의 인스턴스만 포함하는 경우 표준 조건 f(μ(X);Θ) >= 1 − ξ+, 즉, 우리는 SVM이 양수 값을 제공하도록 요구합니다(일부 오분류 허용). 그러나 백 X에 많은 인스턴스가 포함되어 있으면 SVM에 부과되는 임계값이 점점 더 완화됩니다.
[20]에서 같은 저자는 두 단계로 얻은 SbMIL(Sparse Balanced MIL)이라는 두 번째 IS 알고리즘을 제안합니다.:
먼저 MI 데이터에 대해 SMIL 알고리즘을 교육한 다음 결과 인스턴스 수준 분류자 f(x)를 양성 백의 인스턴스에 레이블을 지정하는 데 적용합니다. 이를 위해 점수가 가장 높은 상위 ν 인스턴스는 양수로 레이블이 지정되고 나머지는 음수로 레이블이 지정됩니다. 여기서 ν는 교차 검증에 의해 추정된 매개변수입니다. 이 단계 후에, 표준 SVM 분류기는 최종 분류기 f(x)를 얻는 인스턴스의 결과 훈련 세트를 사용하여 훈련됩니다. 우리는 다른 SVM 기반 IS 분류기에 대해 [20]을 참조하며, 보고된 결과 [20]에 따라 가장 높은 성능을 가진 SbMIL입니다.
4.1.1. Synthetic examples
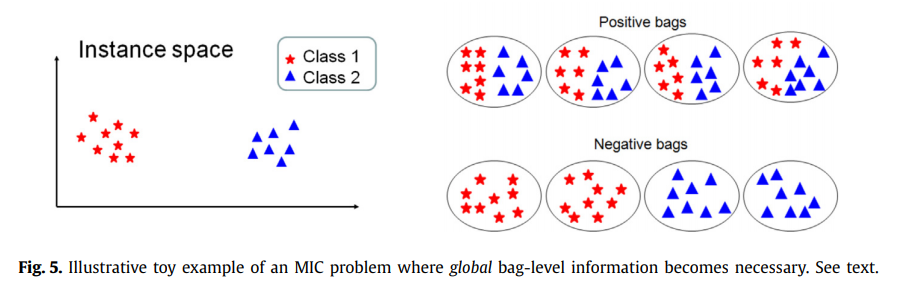
IS 방법은 그림 5와 같은 MI 데이터에 적용할 때 성공적이지 않습니다.
여기에서는 결정을 내리기 전에 전체 가방에 대한 정보를 고려하는 가방 level의 차별적 분류기가 필요합니다. 따라서 모든 IS 방법은 이러한 상황에서 성능이 저하됩니다. 여기에는 아래 섹션 4.2 및 4.2.1에서 설명하는 방법이 포함됩니다.
대조적으로, IS 방법은 긍정적인 가방과 부정적인 가방이 다른 유형의 인스턴스를 갖는 그림 1(a)에 표시된 예에서 성공적일 것입니다. 그림 1(b)에서 우리는 아래에서 검토할 Collective 가정을 따르는 방법으로 얻은 전형적인 결정 경계를 보여주었습니다. 그러나 SMI 기반 방법의 경우 획득된 결정 경계는 그림 8과 유사합니다.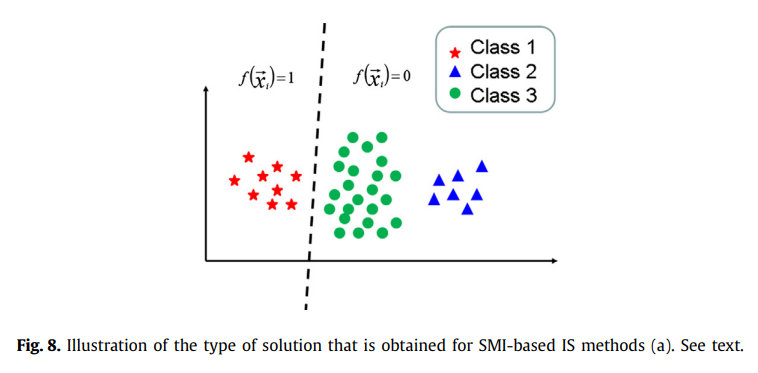
그림 1(b)와 8을 비교하면 후자는 더 비대칭적인 공간 분할을 가지며 여기서 양성 영역은 양성 백에만 나타나는 몇 가지 사례에 더 적합합니다.
4.2. IS methods following the collective assumption
4.2. 집합적 가정에 따른 IS 방법
섹션 4.1의 방법은 마지막 섹션에서 설명한 머스크 약물 분류와 같은 MIC 문제에 뿌리를 둔 표준 MI 가정을 따르며 특정 인스턴스가 백을 긍정적으로 만듭니다. 이는 인스턴스의 나머지 부분이 가방에 대한 관련 정보를 제공하지 않는다는 의미는 아닙니다. 예를 들어 머스크 문제에서 포지티브 백의 모든 인스턴스가 포지티브 백의 특징인 특정 속성을 가질 수 있습니다. 이러한 사실을 바탕으로 보다 정확한 접근 방식은 모든 정보를 활용하여 결정을 내리는 것입니다. 그러나 마지막 섹션의 방법은 특정 인스턴스의 특성(MI-SVM [17]에서와 같이 학습 단계에서 포지티브 백당 하나의 인스턴스만 고려됩니다. 기술 보고서 [19] 참조)만 모델링하거나 양성 백의 평균 벡터만 고려하여(SMIL[20]에서와 같이) 정보의 많은 부분을 버리는 경향이 있습니다.
이 섹션에서는 소위 집합적 가정을 사용하는 IS 방법을 제시합니다. 이 가정은 "가방의 모든 인스턴스가 가방의 레이블에 동등하게 기여한다"[21]라고 말합니다. SMI 가정은 포지티브 백당 몇 개의 인스턴스만 고려하는 반면, Collective 가정은 모든 인스턴스를 고려합니다. 위에서 설명한 것처럼 이러한 유형의 접근 방식은 Musk 데이터베이스를 비롯한 많은 MIC 데이터베이스에서 좋은 결과를 제공할 수 있습니다. 이 데이터베이스에는 특히 관련된 몇 가지 인스턴스가 있을 수 있지만 가방 내부의 모든 인스턴스에는 가방이 긍정적이라는 사실에 대한 정보를 전달하는 특성이 있습니다. 일반적으로 거의 모든 MIC 데이터베이스에서 비슷한 일이 발생합니다.
인스턴스 수준 분류자 f(x)를 추정하기 위해 이 범주의 방법은 각 인스턴스가 가방이 있는 가방의 레이블을 상속하는 인스턴스의 훈련 세트를 사용합니다. 가장 간단한 접근 방식은 Bunescu와 Mooney[20]가 설명한 SIL 알고리즘으로, 결과 훈련 세트에서 표준 지도 분류자 f(x)를 간단히 훈련합니다. 새 백 X가 주어지면 집계 규칙으로 합계를 사용하여 백 수준 분류기 F(X)를 얻습니다.

Xu et al [21]과 Frank와 Xu [22]는 이러한 라인을 따라 몇 가지 방법을 제안했습니다. 이 작업에서 우리는 이 하위 패러다임을 대표하는 단순하고 대표적인 Wrapper MI 방법[22]을 평가합니다. 이 방법의 아이디어는 이전에 설명한 상속 규칙을 사용하여 훈련 세트를 구축하는 것입니다. 이 외에도 각 가방이 동일한 총 중량을 받도록 인스턴스에 가중치가 부여됩니다. 이것은 각 인스턴스 x ∈ X가 가중치 w(x) = S/|X|를 수신하는 경우 달성되며, 여기서 S는 상수입니다. [22]에서 저자는 이 가중치가 좋은 결과를 얻기 위한 기본이라고 주장합니다. 훈련 세트의 다른 가방이 동일한 총 무게를 가지게 하기 때문입니다.
4.2.1. Weighted Collective methods
4.2.1. 가중 집단 방법
이전 접근 방식의 일반화는 각 인스턴스에 대해 다른 가중치를 허용하는 것입니다. 이 일반화는 [10]에서 식별된 것처럼 가중 집단 가정을 발생시킵니다. Foulds[9]와 Mangasarian 및 Wild[23] 모두 이러한 유형의 접근 방식을 따릅니다. 특히 Foulds는 앞에서 설명한 Wrapper MI 알고리즘을 기반으로 하는 IFLIW(Iterative Framework for Learning Instance Weights)를 제안합니다. 이 알고리즘에 대한 자세한 내용은 [9] 및 기술 보고서 [19]를 참조하십시오. 각 인스턴스 x에 대해 가중치 w(x)를 구하면 가방 분류기 F(X)는 인스턴스 수준 응답의 가중 합계로 계산됩니다.

가중 집단 패러다임에 추가하여 Foulds와 Frank [10]는 가중 선형 임계값 패러다임이라고 부르는 것을 식별합니다. [10]에서 설명한 것처럼 이 패러다임은 가중 집합적 패러다임과 거의 동일하며 조금 더 일반적입니다. 그러나 실제로 저자가 이 새로운 패러다임을 구현하기 위해 발견한 유일한 알고리즘은 동일한 저자가 제안한 YARDS 방법[9]입니다. YARDS 알고리즘은 섹션 7에서 볼 수 있듯이 실제로 어휘 기반 알고리즘입니다. 따라서 이 작업에서는 가중 선형 임계값 패러다임을 소개하지 않고 대신 섹션 7에서 YARDS 알고리즘을 설명합니다.
섹션 4.1.1에서 설명한 바와 같이 IS 방법은 판별 분류기가 단일 인스턴스를 넘어선 정보를 고려해야 하는 상황에서 잘 처리되지 않습니다. 이러한 유형의 상황에는 BS 또는 ES 방법이 필요하며 각각 섹션 5와 6에서 검토합니다.
5. Bag-space paradigm
방금 검토한 IS 패러다임의 아이디어는 긍정적인 가방에서 일반적으로 발견되는 것과 부정적인 가방에서 발견되는 것을 구별하여 단일 인스턴스의 속성을 요약하는 모델을 추정하는 것입니다. 이렇게 하면 이러한 유형의 방법이 로컬 정보를 고려하게 됩니다. 즉, 획득한 모델이 bag 전체가 아니라 인스턴스에 관한 것입니다. 분류 시간에 분류기 F(X)는 로컬 응답 f(x)의 집계로 얻어지며, 각 응답은 한 번에 하나의 인스턴스 x만 고려합니다.
이에 반해 BS 패러다임의 방법은 가방 X를 전체적으로 다루며, 판별 학습 과정은 가방의 공간에서 수행된다. 이를 통해 알고리즘은 F(X)의 추론을 수행하는 동안 더 많은 정보를 고려할 수 있습니다.
가방과 같은 비벡터 엔터티를 학습하기 위해 두 개의 가방 X와 Y를 비교하는 거리 함수 D(X,Y)를 정의하고 이 거리 함수를 K-NN 또는 SVM과 같은 표준 거리 기반 분류기에 연결할 수 있습니다. (자세한 내용은 섹션 5.1 참조).
백 X는 d-차원 공간에 있는 점들의 집합일 뿐입니다. 따라서 점 X와 Y의 두 집합을 비교하는 모든 거리 함수 D(X,Y)를 이 컨텍스트에서 사용할 수 있습니다. 이 작업에서 우리는 [24]에서 사용된 최소 Hausdorff 거리, EMD(Earth Movers Distance)[25], Chamfer 거리[26] 및 Gartner et al[14]의 커널을 연구합니다.
먼저 이러한 함수의 정의를 살펴보고 섹션 5.2에서 그 뒤에 있는 직관에 대해 논의합니다. 최소 Hausdorff 거리는 다음과 같이 정의됩니다.

이것은 X와 Y의 가장 가까운 점 사이의 거리입니다.
반면에 EMD 거리는 최적화 프로세스의 결과입니다. X={x_1, ..., x_N}, Y={y_1, ..., y_M}라고 합니다. EMD 거리는 다음과 같이 정의됩니다.

여기서 가중치 w_ij는 일부 제약 조건에 따라 D(X,Y)를 전역적으로 최소화하는 최적화 프로세스를 통해 얻습니다. 자세한 내용은 [27]을 참조하십시오. 모따기 거리는 다음과 같이 정의됩니다.
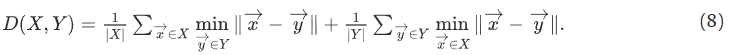
거리 함수 D(X,Y) 외에도 집합 X와 Y 간의 유사도를 제공하는 커널 함수 K(X,Y)를 사용할 수 있습니다.
특히, Gartner et al.[14] 무엇보다도 다음 커널을 제안합니다.

여기서 k(x,y)는 인스턴스 수준 커널이고 p는 이론적으로 가능한 가장 큰 백의 크기와 관련이 있지만 실제로는 교차 검증을 통해 얻을 수 있습니다. 선형, 다항식 또는 가우스 커널과 같은 인스턴스 수준 커널 k(x,y)의 일반적인 정의는 인스턴스 x와 y 간의 유사성 또는 상관 관계 측정을 제공하는 것으로 볼 수 있으므로 백 수준 커널 K(X,Y)는 X의 인스턴스와 Y의 인스턴스 간의 유사성의 합입니다. [14]에서 저자는 인스턴스 x가 인스턴스 레벨 커널에 의해 유도된 공간에서 분리 가능하다면, 백은 식 (9)에서 정의된 백 레벨 커널에 의해 유도된 공간에서도 분리 가능함을 증명합니다. 각 포지티브 백이 적어도 하나의 포지티브 인스턴스를 포함하는 한, 즉 SMI 가정을 달성합니다. 아래에서는 이 커널과 위에서 검토한 거리 모두에서 직관적인 아이디어를 설명합니다.
같은 맥락에서 Zhou et al [28]은 또 다른 커널 함수 K(X,Y)를 제안합니다. 이 커널은 x ∈ X와 y ∈ Y인 쌍(x,y) 사이의 유사성을 사용할 뿐만 아니라 X의 이웃 벡터x와 Y의 이웃 벡터y 사이의 유사성도 사용합니다. 정의는 [28]을 참조하십시오. 다시 말하지만 저자는 이 커널 기능을 SVM과 함께 사용하지만 동일한 커널 기능을 K-NN에서도 사용할 수 있습니다. 결과 알고리즘은 작성자에 의해 MI-Graph라고 합니다.
5.1. Distance-based and kernel-based classifiers
5.1. 거리 기반 및 커널 기반 분류기
언급된 거리 함수는 K-NN과 같은 거리 기반 분류기와 SVM과 같은 커널 기반 분류기와 함께 사용할 수 있습니다. SVM 분류기를 사용하는 경우 거리 D(X,Y)는 확장된 가우스 커널 K(X,Y) = exp(−γ^D(X,Y))를 사용하여 커널 K(X,Y)로 변환할 수 있으며, 여기서 γ는 교차 검증을 통해 추정된 스케일 매개변수입니다.
반대로, 커널 함수는 가방 간의 유사성에 대한 일부 척도를 제공하며 [14]에 설명된 대로 D(X,Y) = √{K(X,X) − 2K(X,Y) + K(Y,Y)} 변환을 사용하여 거리 기반 분류기에 사용할 수 있습니다.
K-NN 및 SVM 외에도 [24]에서 저자는 소위 "인용 K-NN" 분류기를 제안합니다. 이 분류기는 고전적인 K-NN에 대한 작은 수정이며 일반적으로 사용할 수 있습니다(MIC 문제뿐만 아니라).
결과 섹션에서는 일반적으로 더 정확한 SVM 분류자를 사용한 결과를 주로 보여줍니다. 그러나 분류기와 거리 함수의 다양한 조합도 평가합니다. 일반적으로 거리 함수의 정의는 방법의 견고성에 더 큰 영향을 미칩니다. 이러한 의미에서 특정 유형의 거리 함수는 전체 가방에 포함된 정보를 더 잘 활용하므로 SVM을 사용하든 K-NN을 사용하든 일반적으로 분류기를 더 강력하게 만듭니다. 실제로, 거리 함수 D(X,Y)를 정의함으로써(따라서 관련 커널 K(X,Y)를 정의함) 우리는 아래에서 볼 ES 패러다임과 유사하게 원래 가방 공간에서 가방이 설명된 특정 벡터 공간으로 암시적 변환 φ를 제공하고 있습니다.
Foulds와 Frank [10]는 "Nearest Neighbor"(NN)와 MI-Graph의 두 가지 별도 패러다임을 식별합니다(그림 7 참조).
NN 패러다임에는 Citation-KNN과 같은 알고리즘이 포함되어 있는 반면, MI-Graph 패러다임에는 MI-Graph 알고리즘만 포함되어 있습니다. 우리가 본 것처럼, 우리의 BS 패러다임은 NN과 MI-Graph를 특별한 경우로 포함하고 이 두 가지 외에도 몇 가지 다른 경우도 포함하므로 훨씬 더 일반적입니다.
5.2. Synthetic examples
5.2. 합성예
그림 5의 합성 예를 사용하여 서로 다른 거리 함수가 두 개의 가방을 비교하는 방법을 살펴보겠습니다. 섹션 3.3에서 논의한 바와 같이, 이 그림은 가방의 좋은 분류를 얻기 위해 글로벌 가방 수준 정보가 기본인 경우를 보여줍니다. 따라서 다양한 거리 함수가 이 예제에서 어떻게 작동하는지 연구하여 가방에 대한 전역 정보를 활용하는지 확인하는 것은 흥미로울 것입니다.
먼저 식(8)의 모따기 거리를 고려하십시오. 이 거리를 논의하기 위해 인스턴스 x ∈ X와 백 Y 사이의 거리 d(x,Y)를 d(x,Y) = min_(y∈Y) ||x − y||로 정의하겠습니다. x의 클래스와 유사한 클래스에 속하는 인스턴스가 Y에 있는 경우 이 거리는 낮을 것입니다.
이 정의가 주어지면 모따기 거리를 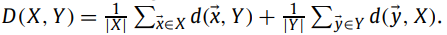
로 다시 쓸 수 있습니다. 따라서 거리 D(X,Y)는 두 개의 백 X와 Y가 동일하거나 유사한 인스턴스 클래스를 갖는 경우 낮을 것입니다.
그림 9(a)에서 이 아이디어는 두 개의 포지티브 백 X와 Y를 비교할 때 설명됩니다.
이 경우 거리 D(X,Y)는 X에 있는 빨간색 별 등급의 각 인스턴스가 Y에 있는 빨간색 별 등급의 일부 인스턴스와 잘 일치하고 파란색 삼각형에서도 동일하게 발생하기 때문에 거리 D(X,Y)가 낮습니다.
그림 9(b)는 포지티브 백 X와 네거티브 백 Y를 비교할 때 발생하는 상황을 보여줍니다. 이 경우 잘 일치하지 않는 인스턴스가 많기 때문에 거리 D(X,Y)가 클 것입니다(특히 X의 파란색 삼각형은 Y의 어떤 인스턴스와도 잘 일치하지 않음).
EMD 및 Gartner et al[14] 방법에서도 비슷한 일이 발생합니다. 전자에서는 두 백 사이의 전역 거리가 최소화되는 방식으로 X의 각 인스턴스를 Y의 가장 유사한 인스턴스와 일치시키는 최적화가 수행됩니다. Gartner et al [14] 방법(Eq. (9))에서 인스턴스 수준 커널 k(x,y) = exp(γ||x − y||)를 고려해 보겠습니다. 여기서 γ는 교차 검증을 통해 얻습니다.
이 경우 γ가 올바르게 추정된 경우 유사한 인스턴스 x 및 y만이 0보다 상당히 큰 값 k(x,y)를 수신합니다. 다시 그 효과는 각 클래스의 인스턴스 비율이 두 백에서 비슷할 경우 두 개의 백 X와 Y가 높은 유사성 점수 K(X,Y)를 받게 된다는 것입니다.
이러한 방법의 예외는 최소 Hausdorff 거리(식(6))로, 두 백에서 가장 가까운 두 인스턴스의 일치 하나만 고려합니다. 이는 그림 9(d)에 설명되어 있습니다. 이 예에서는 다른 백의 인스턴스와 잘 일치하는 한 백의 인스턴스 중 적어도 하나가 있으므로 포지티브 및 네거티브 백 사이의 거리가 낮습니다. 일반적으로 최소 Hausdorff 거리는 단일 베스트 매칭 인스턴스의 정보만 추출하므로 가방의 나머지 부분에서 많은 정보가 누락되기 때문에 많은 상황에서 문제가 됩니다. 실험 섹션에서는 다양한 거리 함수의 효과를 평가합니다.
