[CS] 패리티 비트 & 해밍 코드

패리티 비트 (Parity Bit)

---

패리티 비트는 정보 전달 과정에서 오류가 생겼는지 검사하기 위해 추가된 비트

간단하게 말하면 오류식별자 역할 !

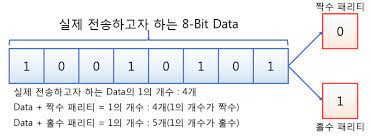
전송하고자 하는 8bit data 외에 추가적으로 패리티 비트 하나를 추가하여 송수신을 한다.

패리티 비트는 종류가 두가지가 있는데 짝수패리티, 홀수패리티로 나누어진다.

짝수패리티와 홀수패리티

패리티 비트에는 0과 1중 하나의 값을 넣을 수 있는데
짝수패리티라고 0이거나 홀수패리티라고 1이 아니다.

• 패리티 비트를 짝수 패리티로 정했을때
  각 비트의 값중에서 1의 개수가 짝수가 되도록 맞춰준다.

  8bit data에서 1의 개수가 3개일때 > 짝수 패리티 : 1

• 패리티 비트를 홀수 패리티로 정했을때
  각 비트의 값중에서 1의 개수가 홀수가 되도록 맞춰준다.

  8bit data에서 1의 개수가 3개일때 > 홀수 패리티 : 0

따라서 패리티비트의 종류에 따라 붙게되는 패리티 비트의 값은 달라진다.

패리티 비트를 추가하는 이유

데이터를 송수신하는 과정 > 각 비트를 단위시간당 하나씩 보내게 되어있다.

이때 오류에 의해서 비트의 값이 틀어져서 1에서 0으로 바뀌거나 0에서 1로 바뀌었을 때 패리티비트를 이용해 확인할 수 있다.

오류 확인 방법

수신된 데이터의 전체 비트를 계산하여 패리티 비트를 다시 계산함으로써 데이터 오류 발생 여부를 알 수 있다.

하지만 패리티 비트는 오류 발생 여부만 알 수 있을뿐, 오류를 수정하거나 고칠 순 없다.

해밍 코드

---

데이터 전송 시 1비트의 에러를 정정할 수 있는 자기 오류정정 코드

오류 발생 여부만 알 수 있었던 패리티 비트를 이용하여 오류 검출과 수정까지 할 수 있다

순서

1. 몇개의 패리티 비트를 추가할지 결정

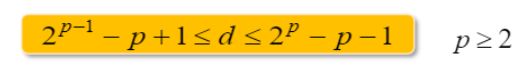
적당한 수의 패리티비트를 구하는 식이다.
p : 패리티비트의 수 , d:데이터 비트의 수

ex) 0101이라는 데이터를 보낼때 패리티 비트는 4개가 적당할까?

위 식에 대입하면
5 <= 4 <= 11
이라는 결과가 나오기 때문에 적절하지 않다.

3을 넣었을땐
2 <= 4 <= 4
의 결과로 3개의 패리티비트는 적절한 수이다.

2. 해밍코드에서 패리티 비트의 위치

해밍코드가 위치하는 자리수는 2의 n제곱의 자리이다.

0101이라는 데이터를 보낼때 3개의 패리티 비트로 정했으므로, 2의 0제곱인 1번째, 2의 1제곱인 2번째, 2의 2제곱인 4번째 자리에 위치하게 된다.

3. 패리티비트의 값 설정하기

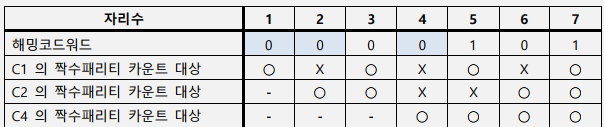
• 첫번째 자리에 위치한 패리티 비트는 자신의 위치부터 자리수(1) 만큼 건너뛰면서 개수를 센다.

3번째 자리 = 0
5번째 자리 = 1
7번째 자리 = 1
------------------
모든 자리의 합 = 2 >> 짝수
따라서 1번째 자리의 해밍코드는 0

• 두번째 자리에 위치한 패리티 비트는 자신의 위치부터 자리수(2) 만큼 건너뛰면서 개수를 센다.

3번째 자리 = 0
6번째 자리 = 0
7번째 자리 = 1
------------------
모든 자리의 합 = 1 >> 홀수
따라서 2번째 자리의 해밍코드는 1

• 네번째 자리에 위치한 패리티 비트는 자신의 위치부터 자리수(4) 만큼 건너뛰면서 개수를 센다.

5번째 자리 = 1
6번째 자리 = 0
7번째 자리 = 1
------------------
모든 자리의 합 = 2 >> 홀수
따라서 4번째 자리의 해밍코드는 0

0101의 올바른 해밍코드는 0100101임을 구할 수 있다.

해밍코드를 이용하여 오류 위치 검출

0100101이 아닌 5번째 위치의 오류 데이터인 0100001을 받았다고 가정했을때 해밍코드는 오류난 곳을 찾을 수 있다.

• 첫번째 패리티비트 자리 확인

0(1번째 자리수) 0(3번째 자리수) 0(5번째 자리수) 1(7번째 자리수) 1이 홀수개 > 1

• 두번째 패리티비트 자리 확인

1(2번째 자리수) 0(3번째 자리수) 0(6번째 자리수) 1(7번째 자리수) 1이 짝수개 > 0

• 네번째 패리티비트 자리 확인

0(4번째 자리수) 0(5번째 자리수) 0(6번째 자리수) 1(7번째 자리수) 1이 홀수개 > 1

결과를 밑에서부터 조합하면 101
10진수로 계산하면 5의 결과가 나오고
5번째 숫자에서 에러가 났음을 확인할 수 있다.

---

• 참고자료
  https://blog.naver.com/miso324/222968617444
  https://blog.naver.com/newzio/222966665706