문제 출처: https://github.com/DA4BAM/dataset
직원 이직 분석
- 최근 이직율이 증가하는 것에 대해 우려를 갖고 있기에, 이직여부에 영향을 주는 요인에 대해 분석하여, 직원들이 회사를 떠나지 않도록 인사 프로그램을 준비하려고 합니다.
- 필요하다면, 검색을 통해 '직원이 회사를 떠나는 이유' 등을 찾아보는 것은 데이터 분석을 하는데 도움이 될 것입니다.
- 이제 제공한 데이터를 바탕으로 각각 개별 변수의 분포를 살펴보며, 비즈니스 인사이트를 최대한 도출해 봅시다.

0.환경설정
1) 라이브러리 로딩
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from statsmodels.graphics.mosaicplot import mosaic
from scipy import stats as spst
import statsmodels.api as sm2) 데이터 로딩
# data data
path = "https://raw.githubusercontent.com/DA4BAM/dataset/master/Attrition_NA.CSV"
data = pd.read_csv(path)
data.drop(['EducationField', 'Education','JobInvolvement', 'StockOptionLevel', 'BusinessTravel','YearsWithCurrManager'
,'YearsInCurrentRole','JobRole', 'Department','EmployeeNumber','EnvironmentSatisfaction','TrainingTimesLastYear','YearsAtCompany']
, axis = 1, inplace = True)
data['Attrition'] = np.where(data['Attrition']=='Yes', 1, 0)
data.head(10)| Attrition | Age | DistanceFromHome | Gender | JobSatisfaction | MaritalStatus | MonthlyIncome | NumCompaniesWorked | OverTime | PercentSalaryHike | RelationshipSatisfaction | TotalWorkingYears | WorkLifeBalance | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 33 | 7.0 | Male | 3 | Married | 11691 | 0.0 | No | 11 | 4 | 14 | 4 |
| 1 | 0 | 35 | 18.0 | Male | 4 | Single | 9362 | 2.0 | No | 11 | 3 | 10 | 3 |
| 2 | 0 | 42 | 6.0 | Male | 1 | Married | 13348 | 9.0 | No | 13 | 2 | 18 | 4 |
| 3 | 0 | 46 | 2.0 | Female | 1 | Married | 17048 | 8.0 | No | 23 | 1 | 28 | 3 |
| 4 | 0 | 39 | NaN | Male | 4 | Divorced | 4127 | 2.0 | No | 18 | 4 | 7 | 3 |
| 5 | 1 | 22 | 4.0 | Male | 3 | Single | 3894 | 5.0 | No | 16 | 3 | 4 | 3 |
| 6 | 0 | 24 | 21.0 | Male | 1 | Divorced | 2296 | 0.0 | No | 14 | 2 | 2 | 3 |
| 7 | 0 | 34 | 8.0 | Male | 3 | Married | 4404 | 2.0 | No | 12 | 1 | 6 | 4 |
| 8 | 0 | 30 | 20.0 | Male | 1 | Married | 9957 | 0.0 | No | 15 | 3 | 7 | 2 |
| 9 | 0 | 26 | 6.0 | Female | 4 | Married | 2659 | 1.0 | Yes | 13 | 3 | 3 | 3 |
| 구분 | 변수 명 | 내용 | type | 비고 |
|---|---|---|---|---|
| Target | Attrition | 이직여부, Yes , No | 범주 | 1- 이직, 0- 잔류 |
| feature | Age | 나이 | 숫자 | |
| feature | DistanceFromHome | 집-직장 거리 | 숫자 | 마일 |
| feature | Gender | 성별 | 범주 | Male, Female |
| feature | JobSatisfaction | 직무 만족도 | 범주 | 1 Low, 2 Medium, 3 High, 4 Very High |
| feature | MaritalStatus | 결혼상태 | 범주 | Single, Married, Divorced |
| feature | MonthlyIncome | 월급 | 숫자 | 달러 |
| feature | NumCompaniesWorked | 입사 전 근무한 회사 수 | 숫자 | 0 - 우리회사가 첫 직장 |
| feature | RelationshipSatisfaction | 동료와의 관계 | 범주 | 1 Low, 2 Medium, 3 High, 4 Very High |
| feature | OverTime | 야근여부 | 범주 | Yes, No |
| feature | PercentSalaryHike | 전년대비 급여인상율 | 숫자 | % |
| feature | TotalWorkingYears | 총 경력 연수 | 숫자 | |
| feature | WorkLifeBalance | 워라밸. 일-삶 균형도 | 범주 | 1 Bad, 2 Good, 3 Better, 4 Best |
1.가설수립
- 각 변수는 직원의 이직여부와 관계가 있을 것이다.
2.단변량 분석
① 변수의 비즈니스 의미
② 숫자? 범주?
③ NaN 존재 여부 및 조치 방안
④ 기초통계량
⑤ 분포
⑥ 위 정보로부터 파악한 내용(비즈니스!) 정리
⑦ 추가 분석해볼 사항 도출
3.이변량 분석
- 자료의 종류에 맞게 X --> Y 에 대해서 그래프(시각화)와 가설검정(수치화)를 수행하고 결과를 평가합니다.
- 가설검정시 다음의 항목을 참조하여 수행합니다.
- 유의수준 : 5%
- 숫자 --> 숫자 : 상관분석
- 범주 --> 범주 : 카이제곱검정
- 범주 --> 숫자 : t검정, 분산분석
- 숫자 --> 범주 : 로지스틱 회귀모형을 통해, 회귀계수의 P.value로 검정을 수행합니다.
- (옵션)자료에 대한 가정 검정.(정규성, 등분산성 등)
target = 'Attrition'(1) 범주형 Feature --> Target
- 모든 범주형 Feature에 대해서 Y와 비교하여 차트를 그리고 수치화 하시오.
① 교차표(pd.crosstab())
② 시각화( Stacked Bar, Mosaic)
③ 가설검정(카이제곱검정) - 각 feature 별로 관계의 정도를 3가지로 정리해봅시다.
1) Gender --> Attrtion
feature = 'Gender'① 교차표(pd.crosstab())
pd.crosstab(data[target], data[feature])| Gender | Female | Male |
|---|---|---|
| Attrition | ||
| 0 | 421 | 629 |
| 1 | 69 | 131 |
② 시각화( Stacked Bar, Mosaic)
temp = pd.crosstab(data[target], data[feature], normalize = 'index')
print(temp)
temp.plot.bar(stacked=True)
plt.axhline(1 - data[target].mean(), color = 'r')
plt.show()Gender Female Male
Attrition
0 0.400952 0.599048
1 0.345000 0.655000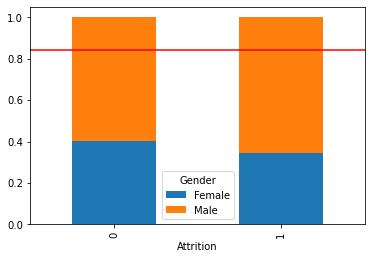
mosaic(data, [feature,target])
plt.axhline(1 - data[target].mean(), color = 'r')
plt.show()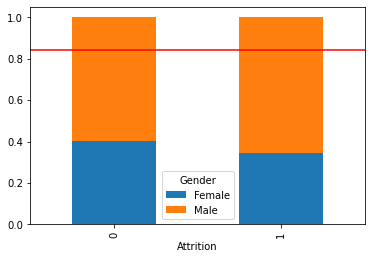
시각화를 통해 파악한 내용을 적어 봅시다.
남성이 여성보다 이직률이 높음을 알 수 있음.
전체 직원의 성별을 비교해보면 남성 근무자가 더 많음을 알 수 있음.
③ 가설검정(카이제곱검정)
# 집계
table = pd.crosstab(data[target], data[feature])
print('교차표\n', table)
print('-' * 100)
# 카이제곱검정
result = spst.chi2_contingency(table)
print('카이제곱통계량', result[0])
print('p-value', result[1])
print('기대빈도\n',result[3])교차표
Gender Female Male
Attrition
0 421 629
1 69 131
----------------------------------------------------------------------------------------------------
카이제곱통계량 1.9782495940105371
p-value 0.15957492990528155
기대빈도
[[411.6 638.4]
[ 78.4 121.6]]④ 시각화와 가설검정을 통해서 파악한 내용을 적어 봅시다.
- 시각화와 수치화로 보았을 때 성별에 따른 이직여부의 관계는 존재한다.
- 여성이 남성보다 이직률이 낮은 이유는 기업의 복지가 좋아서일 수 있음. EX육아휴직 등
- 반대로 남성의 이직률이 높은 것은 복지가 좋더라도 기대에 못 미치는 연봉때문일 수 있음.
2) MaritalStatus --> Attrtion
feature = 'MaritalStatus'① 교차표(pd.crosstab())
pd.crosstab(data[feature], data[target])| Attrition | 0 | 1 |
|---|---|---|
| MaritalStatus | ||
| Divorced | 253 | 23 |
| Married | 501 | 69 |
| Single | 296 | 108 |
② 시각화( Stacked Bar, Mosaic)
temp = pd.crosstab(data[feature], data[target], normalize = 'index')
print(temp)
temp.plot.bar(stacked = True)
plt.axhline(1 - data[target].mean(), color = 'r')
plt.show()Attrition 0 1
MaritalStatus
Divorced 0.916667 0.083333
Married 0.878947 0.121053
Single 0.732673 0.267327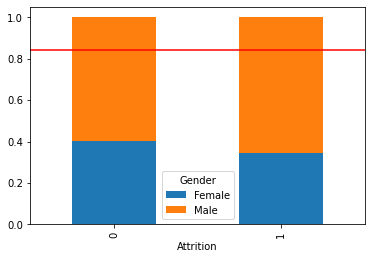
mosaic(data, [feature,target])
plt.axhline(1 - data[target].mean(), color = 'r')
plt.show()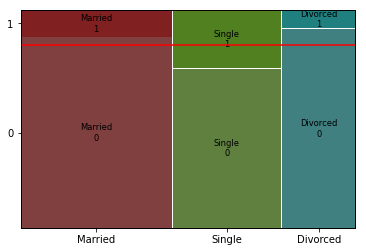
시각화를 통해 파악한 내용을 적어 봅시다.
- 결혼 상태에 따른 이직률의 차이가 존재함을 알 수 있음.
- 특히 미혼일수록 이직률이 높음을 알 수 있음.
- 반면 결혼하거나 이혼경력이 있는 이들의 경우 이직률의 비율이 다른 결혼 상태에 비해 상대적으로 낮음을 볼 수 있음.
③ 가설검정(카이제곱검정)
# 집계
table = pd.crosstab(data[feature], data[target])
print('교차표\n', table)
print('-' * 100)
# 카이제곱검정
result = spst.chi2_contingency(table)
print('카이제곱통계량', result[0])
print('p-value', result[1])
print('기대빈도\n',result[3])교차표
Attrition 0 1
MaritalStatus
Divorced 253 23
Married 501 69
Single 296 108
----------------------------------------------------------------------------------------------------
카이제곱통계량 53.12935546374186
p-value 2.9047385436211595e-12
기대빈도
[[231.84 44.16]
[478.8 91.2 ]
[339.36 64.64]]④ 시각화와 가설검정을 통해서 파악한 내용을 적어 봅시다.
- 시각화와 가설검정 모두 결혼상태에 따른 이직률에 관계가 있는 것을 확인할 수 있음.
- 앞서 언급한 것처럼 결혼을 하거나 이혼 경력이 있는 이들의 비율이 미혼인 이들보다 상대적으로 이직률이 낮음을 볼 수 있는데, 이는 결혼한 상태로 더 안정적인 직장을 원하는 경향이 반영된 것으로 보임.
- 결혼한 이들과 이혼경력이 있는 이들의 이직 성향이 비슷하기 때문에 미혼인 이들의 이직의 대한 원인이 연봉에 있는 것인지, 아니면 개인으로서 받을 수 있는 회사 복지에 대한 문제인지 파악할 필요가 있음.
3) JobSatisfaction --> Attrtion
feature = 'JobSatisfaction'① 교차표(pd.crosstab())
pd.crosstab(data[feature], data[target])| Attrition | 0 | 1 |
|---|---|---|
| JobSatisfaction | ||
| 1 | 197 | 53 |
| 2 | 196 | 39 |
| 3 | 308 | 60 |
| 4 | 349 | 48 |
② 시각화( Stacked Bar, Mosaic)
temp = pd.crosstab(data[feature], data[target], normalize = 'index')
print(temp)
temp.plot.bar(stacked=True)
plt.axhline(1 - data[target].mean(), color = 'r')
plt.show()Attrition 0 1
JobSatisfaction
1 0.788000 0.212000
2 0.834043 0.165957
3 0.836957 0.163043
4 0.879093 0.120907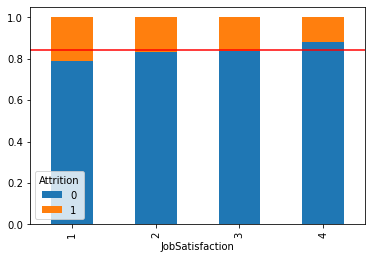
mosaic(data, [feature,target])
plt.axhline(1 - data[target].mean(), color = 'r')
plt.show()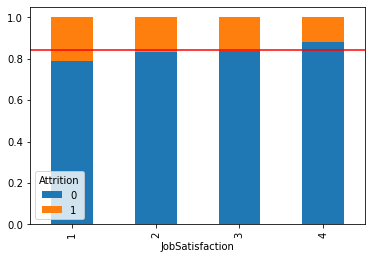
시각화를 통해 파악한 내용을 적어 봅시다.
- 직업 만족도에 따라 이직률의 차이가 있음을 확인할 수 있음.
- 직업 만족도가 제일 낮은 1의 경우 이직률의 비율이 다른 만족도보다 높음.
- 직업 만족도가 제일 높은 4의 경우 이직률의 비율이 다른 만족도보다 낮음.
- 전체 만족도의 비율을 확인했을 때 업무 만족도가 높은(3, 4)의 비율이 약 과반을 넘음.
- 그러나 전체 만족도의 비율 중 만족도가 낮은(1, 2)의 비율도 적지 않음.
③ 가설검정(카이제곱검정)
# 집계
table = pd.crosstab(data[feature], data[target])
print('교차표\n', table)
print('-' * 100)
# 카이제곱검정
result = spst.chi2_contingency(table)
print('카이제곱통계량', result[0])
print('p-value', result[1])
print('기대빈도\n',result[3])교차표
Attrition 0 1
JobSatisfaction
1 197 53
2 196 39
3 308 60
4 349 48
----------------------------------------------------------------------------------------------------
카이제곱통계량 9.63151465436614
p-value 0.021972649369306214
기대빈도
[[210. 40. ]
[197.4 37.6 ]
[309.12 58.88]
[333.48 63.52]]④ 시각화와 가설검정을 통해서 파악한 내용을 적어 봅시다.
- 직업만족도에 따른 이직률의 차이가 있음을 확인할 수 있음.
- 전체 만족도를 높은편(3, 4), 낮은편(1, 2)로 보았을 때 둘의 비율이 크게 차이 나지 않음.
- 따라서 업무 만족도를 높이기 위한 방안이 필요해 보임.
(2) 숫자형 Feature --> target
- 숫자형 Feature에 대해서 Y와 비교하여 차트를 그리고 수치화 하시오.
① 그래프 : histogram, densityplot
② 수치화 : 로지스틱회귀
1) Age --> Attrtion
feature = 'Age'① 그래프 : histogram, densityplot
sns.histplot(x=feature, data = data, hue = target)
plt.show()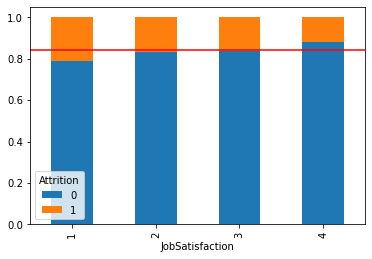
sns.kdeplot(x=feature, data = data, hue = target, common_norm = False)
plt.show()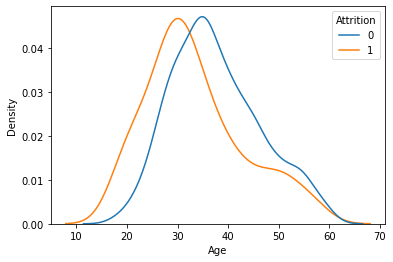
시각화를 통해 파악한 내용을 적어 봅시다.
연령대에 따른 이직률의 관계가 보임
- 20대 중반부터 30대 중반까지의 이직률이 높게 분포해 있음을 알 수 있음.
- 40대 역시 전후 나이대보다 높은 이직률을 보임.
- 이후 높은 연령대에서의 이직률은 점차 감소함
② 수치화 : 로지스틱회귀
model = sm.Logit(data[target], data[feature])
result = model.fit()
print(result.pvalues)Optimization terminated successfully.
Current function value: 0.424660
Iterations 5
Age 4.667821e-100
dtype: float64③ 시각화와 수치화를 통해 파악한 내용을 적어 봅시다.
- 연령대에 따른 이직률의 관계가 존재함.
- 20대 중반부터 30대 중반의 연령대는 회사에서 실무를 담당하는 인재들임.
- 그런데 이들의 이직률이 고르고 높게 분포되어 있다는 것은 주변 회사에서 더 높은 연봉을 제시해 스카웃해가는 것이라 볼 수 있음.
- 또한 40대의 경우 회사의 중역을 맡는 관리자 급이기 때문에 타 회사에 역시 스카웃 제의가 올 확률이 높음.
2) DistanceFromHome --> Attrtion
feature = 'DistanceFromHome'
temp = data.loc[data[feature].notnull()]① 그래프 : histogram, densityplot
sns.histplot(x=feature, data = temp, hue = target)
plt.show()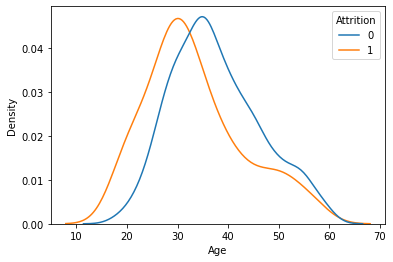
sns.kdeplot(x=feature, data = temp, hue = target, common_norm = False)
plt.show()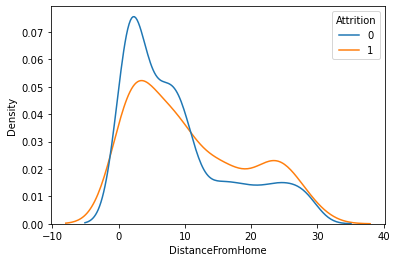
시각화를 통해 파악한 내용을 적어 봅시다.
- 거주지에서 직장으로부터의 거리가 짧을수록 이직률이 낮음을 알 수 있음.
- 대체적으로 직장에서 거주지로부터의 거리가 15 이하에 많이 분포되어 있음
- 그러나 15 ~ 25 처럼 점점 회사에서 거주지가 멀어질수록 이직하는 비율도 높아짐.
- 이후 완전 멀리 있는 25 이후 부터는 이직률이 다시 감소함 (가족들과 사는 직원일 수 있음)
② 수치화 : 로지스틱회귀
temp = data.loc[data[feature].notnull()]
model = sm.Logit(temp[target], temp[feature])
result = model.fit()
print(result.pvalues)Optimization terminated successfully.
Current function value: 0.568793
Iterations 6
DistanceFromHome 2.694280e-44
dtype: float64③ 시각화와 수치화를 통해 파악한 내용을 적어 봅시다.
- 거주지에서 직장으로부터의 거리가 짧을 수록 이직률이 낮음을 알 수 있음.
- 전체 직원중 매우 가까이 살고 있는 직원들이 많기 때문에 회사에서 따로 제공하는 기숙사가 존재할 수도 있음.
- 그렇지 않은 이들의 경우 주로 이직률이 높은 15 ~ 20만큼의 거리에 있는 거주지에 지내고 있을 확률도 있음.
- 또한 많이 떨어진 곳에 살고 있는 이들의 이직률은 낮은데 이는 가족 구성원(자녀 학교 등) 때문에 그런 것일 수 있음.
3) MonthlyIncome --> Attrtion
feature = 'MonthlyIncome'① 그래프 : histogram, densityplot
sns.histplot(x = feature, data = data, hue = target)
plt.show()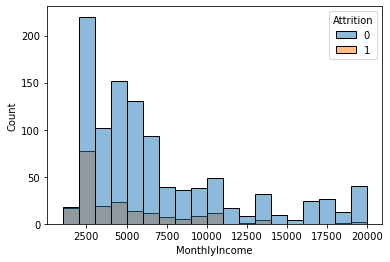
sns.kdeplot(x = feature, data = data, hue = target, common_norm = False)
plt.show()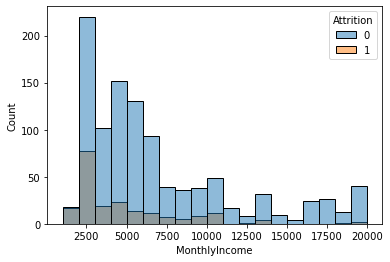
시각화를 통해 파악한 내용을 적어 봅시다.
- 월별 소득이 낮은 (0 ~ 3000) 구간의 이직률이 매우 높음을 알 수 있음.
- 또한 5000~ 10000대 구간 역시 관리자 급들이 분포하고 있는 구간으로 추측 가능하며 경쟁사의 스카웃 제의가 들어올 가능성이 높음.
- 고액의 연봉을 받는 임원일수록 이직률이 기하급수적으로 낮아짐.
② 수치화 : 로지스틱회귀
model = sm.Logit(data[target], data[feature])
result = model.fit()
print(result.pvalues)Optimization terminated successfully.
Current function value: 0.437401
Iterations 6
MonthlyIncome 1.922717e-71
dtype: float64③ 시각화와 수치화를 통해 파악한 내용을 적어 봅시다.
- 이직률과 월급 간에는 관계가 존재한다.
- 월급이 매우 적은 구간이 보이는데, 혹시 회사 환경관리를 해주는 청소부분들의 연봉도 포함인건지 확인해 봐야함.
- 신입부터 관리자급의 연봉(2500 ~ 7500)의 경우 해당 업무에 맡는 임금을 주고 있는지 경쟁사와 비교해 볼 필요가 있음.
4.관계 정리
1) 강한관계의 변수
MaritalStatus, Age, DistanceFromHome, MonthlyIncome
2) 중간관계의 변수
Gender, JobSatisfaction
