[프로그래머스][87946] 피로도
완전탐색 (brute force) & 깊이우선탐색 (DFS)
일주일만에 완전 탐색 문제 푸니까 살짝 헷갈렸다.
그냥 무식하게 전부 다 검색하는 방법으로 해결!
좀 더 세세한 조건을 걸어서 해보고 싶으나, 던전의 최대 개수가 8개로 적기 때문에 완전 탐색으로 단순히 해결했다.
# k = 현재 피로도
# dungeons = [최소필요피로도, 소모피로도]의 2차원 배열
# 예: 80, [[80, 20], [50, 40], [30, 10]]
def dfs(k, cnt, dungeons, visited):
global answer
answer = max(answer, cnt)
for i in range(len(dungeons)):
req, con = dungeons[i]
if visited[i] == False and req <= k:
visited[i] = True
dfs(k-con, cnt+1, dungeons, visited)
visited[i] = False
def solution(k, dungeons):
global answer
visited = [False] * len(dungeons)
answer = 0
dfs(k, 0, dungeons, visited)
return answer[프로그래머스][49189] 가장 먼 노드
그래프 & 너비우선탐색(BFS)
DFS, BFS 하면서 다 한 번씩 해봤던 개념이라 어렵지 않다고 생각했는데,
이리저리 에러가 꽤 나서, 생각보다 시간은 꽤 걸렸다.
문제에서 요구하는대로, 노드 1에서 각 노드까지의 거리를 저장하기 위해 distances 리스트를 만들고,
각 노드에서 연결된 노드 번호 리스트인 graph를 만들었다.
양방향 그래프이므로, 양쪽 노드에 모두 연결되어있음이 기록되어야 한다.
[[3, 6], [4, 3], [3, 2], [1, 3], [1, 2], [2, 4], [5, 2]]
위와 같은 입력값이 들어오면,
graph는 [[],[3,2],[3,1,4,5],[6,4,2,1],[3,2],[2],[3]] 이 된다.
그리고 너비 우선 탐색(BFS)을 하기 위해, queue를 만들고 큐가 빌 때까지 반복하면 된다.
# 노드의 개수 n, 간선에 대한 정보가 담긴 2차원 배열 edge
# 예시 : [[3, 6], [4, 3], [3, 2], [1, 3], [1, 2], [2, 4], [5, 2]]
from collections import deque
def solution(n, edge):
# 노드 1부터 각 노드까지의 거리 리스트
distances = [0] * (n+1)
# 각 노드에서 연결된 노드 번호 리스트
graph = [[] for _ in range(n+1)]
# 연결된 노드 정보 저장
for e in edge:
graph[e[0]].append(e[1])
graph[e[1]].append(e[0])
queue = deque()
queue.append(1)
distances[1] = 1
while queue:
now = queue.popleft()
for linked in graph[now]:
if distances[linked] == 0:
distances[linked] = distances[now] + 1
queue.append(linked)
answer = distances.count(max(distances))
return answer[프로그래머스][12977] 소수 만들기
def solution(nums):
answer = 0
for i in range(len(nums)-2): # 첫번째 숫자
for j in range(i+1, len(nums)-1): # 두번째 숫자
for k in range(j+1, len(nums)): # 세번째 숫자
sum = nums[i] + nums[j] + nums[k]
for n in range(2, sum//2):
if sum % n == 0:
break
else: # for문 다 돌고 나서 실행 (break 있으면 실행 안함)
answer += 1
return answer[프로그래머스][49191] 순위
나는 wins 와 loses 리스트에 각자 이긴 사람과 진 사람 리스트를 담아서 문제를 해결했다.
N번 선수가 이긴 선수 M번에게 진 선수들은 N번도 이기게 되므로,
그렇게 N이 이기고 지는 선수들을 각각 담아,
결과적으로 N이 이기고 질 수 있는 선수들의 수가 전체 선수의 수 - 1 이면 해당 선수의 순위를 알 수 있다.
구글링을 해보니 플로이드 워셜 알고리즘을 써서 해결할 수 있다는데, 내가 이 알고리즘을 아직 모르다보니 적용할 수가 없었다.
공부할 게 하나 더 늘었다...!
# 예시 n = 5, results = [[4, 3], [4, 2], [3, 2], [1, 2], [2, 5]]
def solution(n, results):
answer = 0
wins = [[] for _ in range(n+1)] # 1번 인덱스에는 1이 이긴(1에게 진) 선수가 담김
loses = [[] for _ in range(n+1)] # 1번 인덱스에서는 1이 진(1에게 이긴) 선수가 담김
for winner, loser in results:
wins[winner].append(loser)
loses[loser].append(winner)
# wins = [[], [2], [5], [2], [3, 2], []]
# loses = [[], [], [4, 3, 1], [4], [], [2]]
for i in range(1, n+1):
for w in wins[i]:
# 1 > 2 > 5 (1이 2에게 이겼다면, 2에게 진 애들도 모두 1이 이긴다)
for a in wins[w]:
if a not in wins[i]:
wins[i].append(a)
# 한 바퀴 돌면 [[], [2, 5], [5], [2], [3, 2], []]
for l in loses[i]:
for b in loses[l]:
if b not in loses[i]:
loses[i].append(b)
# 3이 4에게 졌다면, 4에게 이긴 애들도 모두 3을 이긴다 (3이 짐)
print(wins)
print(loses)
# wins = [[], [2, 5], [5], [2, 5], [3, 2, 5], []]
# loses = [[], [], [4, 3, 1], [4], [], [2, 4, 3, 1]]
for i in range(1, n+1):
if len(wins[i]) + len(loses[i]) == n-1:
answer += 1
return answer[백준][1743] 음식물 피하기
너비우선탐색(BFS) 활용
예전에 전투 문제랑 비슷했다.
전투 때 고생해서 풀었더니, 이제 BFS는 그래도 무난하게 쉽게 푼 듯!
import sys
from collections import deque
sys.stdin = open("sample_input.txt", "r")
# 세로 길이 n, 가로 길이 m, 음식물 쓰레기 개수 k
n, m, k = map(int, sys.stdin.readline().split())
graph = [[0] * m for _ in range(n)]
for _ in range(k):
x, y = map(int, sys.stdin.readline().split())
x, y = x-1, y-1
graph[x][y] = 1
# graph = [[1, 0, 0, 0], [0, 1, 1, 0], [1, 1, 0, 0]]
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
size = 0
def bfs(x, y):
queue = deque([(x, y)])
graph[x][y] = 2 # 방문한 곳은 2로 바꿈
count = 1
while queue:
x, y = queue.popleft()
for i in range(4):
nx, ny = x + dx[i], y + dy[i]
if 0 <= nx < n and 0 <= ny < m:
if graph[nx][ny] == 1:
queue.append((nx, ny))
graph[nx][ny] = 2
count += 1
return count
for i in range(n):
for j in range(m):
if graph[i][j] == 1:
size = max(bfs(i, j), size)
print(size)[프로그래머스][43105] 정수 삼각형
from collections import deque
def solution(triangle):
height = len(triangle)
answers = [[0 for _ in range(len(tri))] for tri in triangle]
for i in range(height):
for j in range(len(triangle[i])):
before = 0
if i - 1 >= 0:
if j == 0:
before = answers[i-1][j]
elif 0 < j < len(triangle[i])-1:
before = max(answers[i-1][j-1], answers[i-1][j])
elif j == len(triangle[i]) - 1:
before = answers[i-1][j-1]
sum = triangle[i][j] + before
answers[i][j] = sum
# [[7], [10, 15], [18, 16, 15], [20, 25, 20, 19], [24, 30, 27, 26, 24]]
return max(answers[-1])[프로그래머스][49190] 방의 개수
와 이거 짱 어려웠다..

처음에 이렇게만 해결했는데..
그랬더니 실패가 떴다..
구글링을 해봤더니 대각선끼리 만나는 경우가 해결이 되지 않기 때문!!
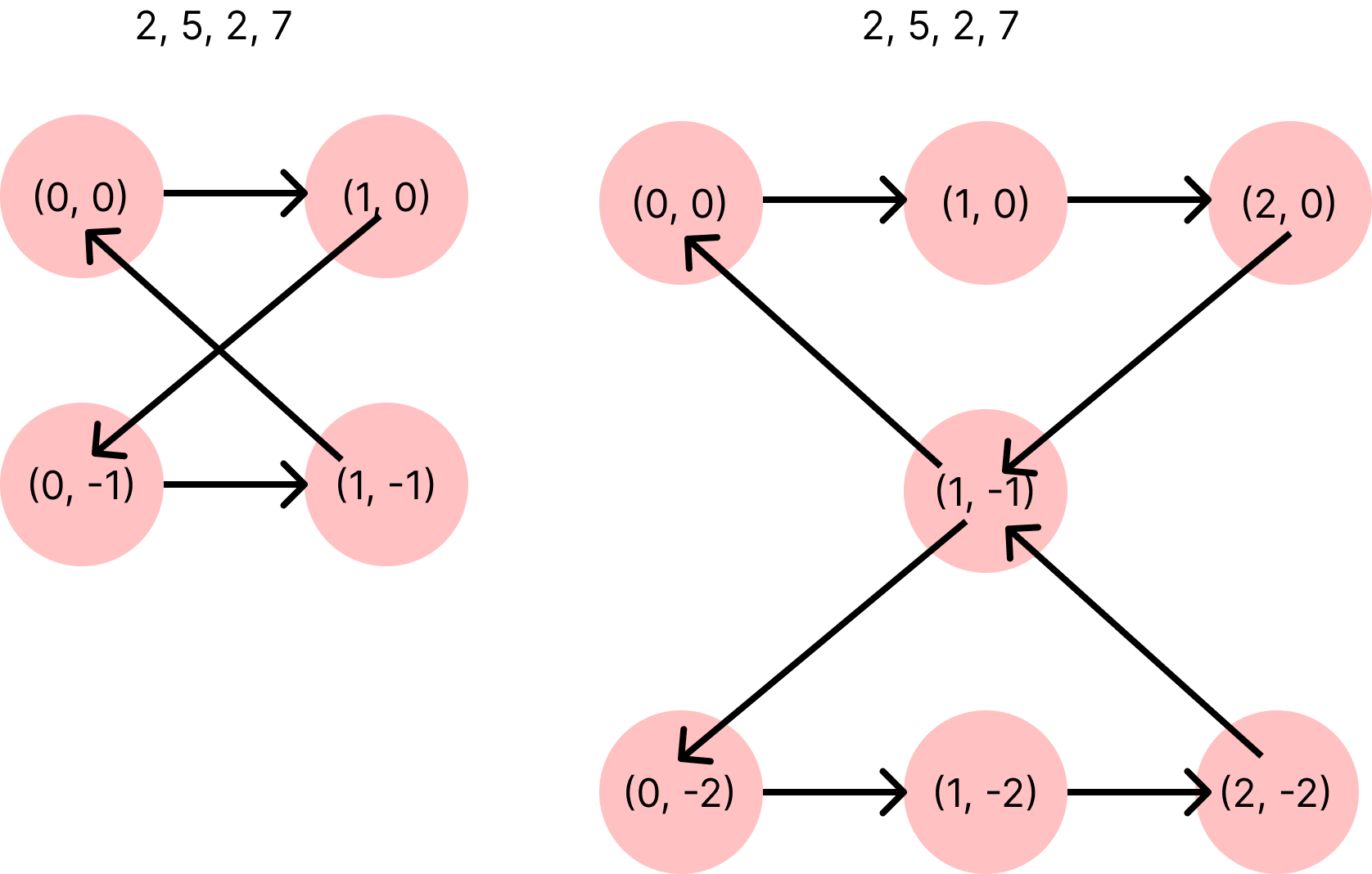
그래서 이렇게 각 이동당 두번씩 움직이게 해서 점을 찍으면,
대각선이 만나는 경우에도 체크를 할 수 있다.
def solution(arrows):
graph = {(0, 0): []} # 시작점 (0,0)
move = {
0: [0, 1],
1: [1, 1],
2: [1, 0],
3: [1, -1],
4: [0, -1],
5: [-1, -1],
6: [-1, 0],
7: [-1, 1]
}
room = 0
x, y = 0, 0
# print((0, 0) in graph) -> True
# print((1, 0) in graph) -> False
for arr in arrows:
for _ in range(2):
nx, ny = x + move[arr][0], y + move[arr][1]
if (nx, ny) in graph and (x, y) not in graph[(nx, ny)]:
room += 1
graph[(nx, ny)].append((x, y))
graph[(x, y)].append((nx, ny))
elif (nx, ny) not in graph:
graph[(nx, ny)] = [(x, y)]
graph[(x, y)].append((nx, ny))
x, y = nx, ny
# print(graph)
return room[프로그래머스][43162] 네트워크
BFS로 시도하다가 삽질하고, DFS로 해결함.
BFS로도 가능은 할 것 같은데.. 일단은 스루한닷!
def solution(n, computers):
answer = 0
visited = [False for _ in range(n)]
def dfs(com):
if visited[com]:
return
visited[com] = True
for w in range(n):
if w != com and computers[com][w] == 1:
if visited[w] == False:
dfs(w)
for i in range(n):
if visited[i] == False:
dfs(i)
answer += 1
return answer[백준][11724] 연결 요소의 개수
깊이우선탐색(DFS), 너비우선탐색(BFS)
DFS와 BFS 모두 적용 가능하다.
이미지에서 위가 BFS, 아래가 DFS로 푼 것이고,
메모리 면에서는 DFS가, 시간 면에서는 BFS가 성능이 좋았다.
BFS 코드
import sys
from collections import deque
# sys.setrecursionlimit(10**7)
# sys.stdin = open("sample_input.txt", "r")
# 정점 개수 n, 간선 개수 m
n, m = map(int, sys.stdin.readline().split())
graph = [[] for _ in range(n+1)]
visited = [False for _ in range(n+1)]
for _ in range(m):
x, y = map(int, sys.stdin.readline().split())
graph[x].append(y)
graph[y].append(x)
# graph : [[], [2, 5], [1, 5], [4], [3, 6], [2, 1], [4]]
count = 0
def bfs(node):
queue = deque([node])
visited[node] = True
while queue:
now = queue.popleft()
for n in graph[now]:
if not visited[n]: # False라면
queue.append(n)
visited[n] = True
for i in range(1, n+1):
if not visited[i]:
bfs(i)
count += 1
print(count)DFS 코드
import sys
# from collections import deque
sys.setrecursionlimit(10**7)
# sys.stdin = open("sample_input.txt", "r")
# 정점 개수 n, 간선 개수 m
n, m = map(int, sys.stdin.readline().split())
graph = [[] for _ in range(n+1)]
visited = [False for _ in range(n+1)]
for _ in range(m):
x, y = map(int, sys.stdin.readline().split())
graph[x].append(y)
graph[y].append(x)
# graph : [[], [2, 5], [1, 5], [4], [3, 6], [2, 1], [4]]
count = 0
def dfs(node):
if visited[node]: # 탈출 조건
return
visited[node] = True
for n in graph[node]:
if visited[n] == False:
dfs(n)
for i in range(1, n+1):
if visited[i] == False:
dfs(i)
count += 1
print(count)[백준][2644] 촌수계산
깊이우선탐색 (DFS)
괜히 꼬아서 생각해서 시간이 오래 걸렸는데, 그냥 무난무난한 문제였던 것 같다.
하지만 난 BFS보다 DFS가 더 어려운 것 같다 ㅠㅠ
import sys
# sys.setrecursionlimit(10**7)
# sys.stdin = open("sample_input.txt", "r")
# 전체 사람의 수 n
n = int(sys.stdin.readline())
# 촌수 계산을 하는 두 사람
p1, p2 = map(int, sys.stdin.readline().split())
# 부모 자식 간의 관계의 개수 m
m = int(sys.stdin.readline())
graph = [[] for _ in range(n+1)] # n번 인덱스의 부모가 담김
visited = [False for _ in range(n+1)]
for _ in range(m):
x, y = map(int, sys.stdin.readline().split())
graph[y].append(x)
graph[x].append(y)
# graph : [[], [2, 3], [1, 7, 8, 9], [1], [5, 6], [4], [4], [2], [2], [2]]
def dfs(node, count=0):
# global answer
# print(node, count)
visited[node] = True
if node == p2:
# answer = count
return count
for g in graph[node]:
if not visited[g]:
temp = dfs(g, count+1)
if temp != -1:
return temp
return -1
print(dfs(p1))