Dynamic Programming (DP)
큰 문제를 작은 문제로 나눠서 푸는 알고리즘으로 피보나치 수열이 한 종류이다.
DP로 문제를 풀려면,
1. Overlapping Subproblem
- 큰 문제와 작은 문제를 같은 방법으로 해결 가능하다.
- 큰 문제를 작은 문제로 쪼갤 수 있다.
2. Optimal Substructure
큰 문제의 정답을 작은 문제의 정답에서 구할 수 있다.
따라서 같은 문제를 여러번 풀 필요가 없다 → 답을 저장해 놓으면 된다!
- Tabulation → dp[i][j]와 같은 dp 테이블을 만들 수 있다.
- Memoization
피보나치 수열
-
Memoization 없을 때,
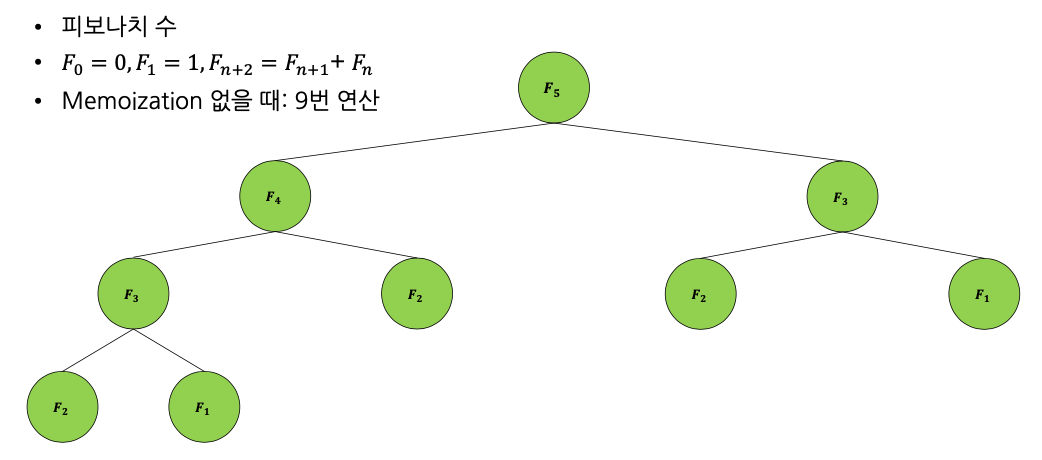
-
Memoization 있을 때,
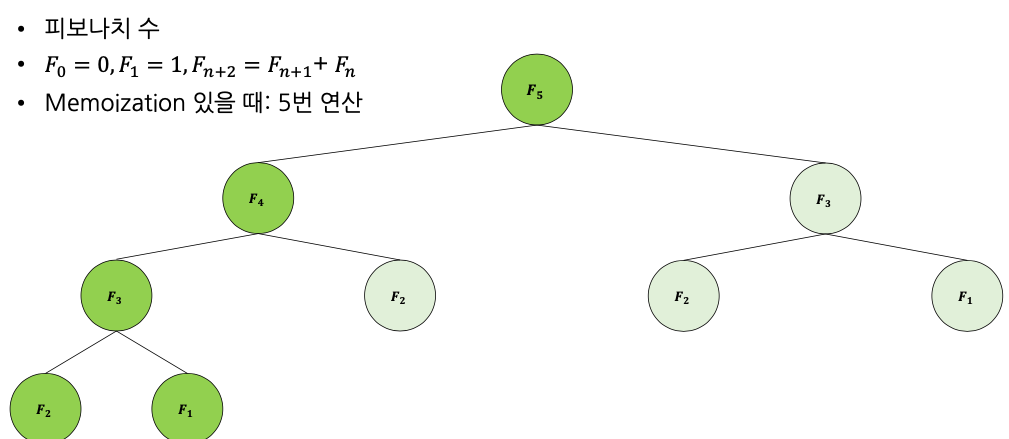
피보나치 수에서 DP 이용해 시간 복잡도의 차이
O(2^n) → O(N)
DP 문제 풀이 전략
- DP식 정의
- 초기 조건 찾기
- 점화식 세우기
dp[i] := i번째 피보나치 수열
dp[0] = 0, dp[1] = 1
dp[i] = dp[i-1] + dp[i-2]
DP 구현하기
- 코드의 실행 순서로 구분한다.
- Top-Down : 큰 문제부터 시작
주로 재귀 함수를 이용해 구현, 시간이 더 걸리지만 구현이 더 직관적이다.
int dp[100];
int f(int n) {
if (dp[i] != -1) return dp[i];
if (i <= 1) return dp[i] = i; // 초기조건
return dp[i] = f(i-1) + f(i-2); // 점화식
}dp 테이블의 값을 -1로 초기화한 후, 재귀함수를 부른다.
왜냐하면 어떤 답을 구했으면 다시 계산할 필요가 없기 때문에 그걸 구분하는 요소로 -1을 사용한다.
- Bottom-Up : 작은 문제부터 시작
주로 반복문을 이용해 구현
int dp[100];
int f(int n) {
dp[0] = 0, dp[1] = 1; // 초기조건
for (int i = 2; i <= n; i++) {
dp[i] = dp[i-1] + dp[i-2]; // 점화식
}
return dp[n];
}-
LIS(Longest Increasing Sequence) : DP로 풀 때, O(N^2)
dp[i] := i번째 원소를 마지막으로 하는 LIS 길이
dp[1] = 1
dp[i] = max(dp[j] + 1) (0 <= j < i, a[i] > a[j]) -
LCS(Longest Common Sequence) : DP로 풀 때, O(N^2)
dp[i][j] := a[i], b[j]까지의 LCS
dp[i][j] = 0 (i = 0, j = 0)
dp[i][j]
= max(dp[i-1][j], dp[i][j-1], dp[i-1][j-1] + 1) (a[i] = b[j])
= max(dp[i-1][j], dp[i][j-1]) (a[i] =/= b[j])
실제 DP 테이블을 채워보면,
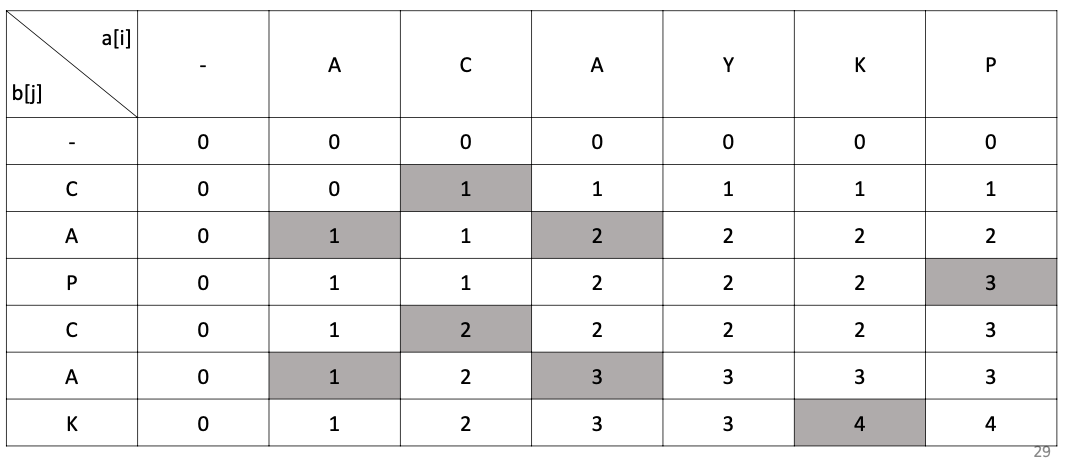

좋은 글 감사합니다. 자주 방문할게요 :)