[Algorithm] day6. Binary Search, Divide and Conquer

이분탐색

• 선형 탐색
  데이터를 처음부터 끝까지 차례대로 순회하면서 자료를 탐색하는 방법
  자료의 수가 N개면, O(N)

이분 탐색 (Binary Search)

정렬된 자료에서만 사용가능하다.
매번 탐색 범위를 절반씩 줄이면서 탐색하기 때문에 원하는 자료가 있는지 O(logN)에 판별할 수 있다.
탐색을 여러번 해야할 때 효율적이다.

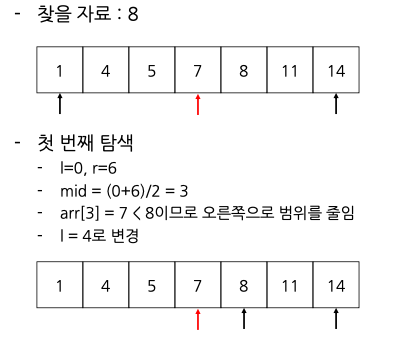
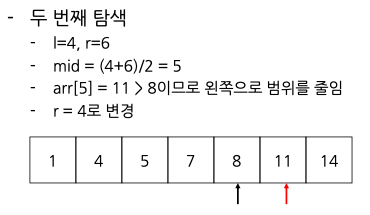
이분 탐색 과정

• 찾으려고 하는 자료의 값을 x라고 하면
• 처음 탐색 범위는
  start = 1, end = N(N은 자료의 길이)
• start <= end인 동안 탐색 과정을 계속 반복한다.
  mid = (start + end) / 2
  case)
  arr[mid] < x 이면, [l, mid]에는 원하는 자료가 없다. 따라서 start = mid + 1로 변경한다.
  arr[mid] = x 이면, 원하는 자료를 찾았다.
  arr[mid] > x 이면, [mid, r]에는 원하는 자료가 없다. 따라서 end = mid - 1로 변경한다.

시간복잡도는 O(logN)이다.

이분 탐색 코드

a.sort()

for num in b:
    start = 0
    end = n - 1
    isExist = False

    while start <= end:
        mid = (start + end) // 2
        if (num == a[mid]):
            isExist = True
            print(1)
            break
        elif num > a[mid]:
            start = mid + 1
        else:
            end = mid - 1

    if not isExist:
        print(0)

파라메트릭 서치 (Parametric Search, 매개 변수 탐색)

• 최적화 문제 : 가능한 답 중에서 최솟값 또는 최댓값을 구하는 문제
• 결정 문제 : 네 또는 아니요로 답할 수 있는 문제

최적화 문제를 결정 문제로 바꾸어 푸는 기법으로
특정 문제 상황(최적화 문제)에서 답을 직접 구하는 것이 아니라, "이게 답이 될 수 있는가? [Y/N]"(결정 문제)를 반복 확인하여 최솟값 또는 최댓값을 구한다.

이때, 결정 문제에 대한 답이 단조성을 가지는 경우(계속 YES가 나오다가 그 이후로 쭉 NO만 나오거나 그 반대여야 한다.)에만 이분탐색으로 해결할 수 있다.

분할정복

큰 문제를 더 작은(쉬운) 문제로 분할하고 부분 문제의 답을 결합하여 큰 문제의 답을 구하는 알고리즘으로
보통 재귀함수로 구현하면 편리하다.

• 분할 : 재귀 함수를 다시 호출
• 정복 : 재귀 함수의 종료 조건 (base case)
• 결합 : 재귀 함수의 결과값을 바탕으로 답을 계산

분할정복 예시

• 정렬 : 병합 정렬, 퀵 정렬
• 탐색 : 이분 탐색

분할정복 응용
빠른 거듭제곱 : 정수 a, n에 대하여 a^n을 계산하는 방법
재귀함수를 아래와 같이 정의해보면,
F(a, n) = a^n

• base case ) n = 0이면, 1을 반환한다.
• general case
  n이 짝수라면, 지수 법칙에 의해 a^n = a^(n/2) a^(n/2)
  n이 홀수라면, 비슷하게 a^n = a^(n/2) a^(n/2) a
  n이 짝수, F(n) = F(n/2)^2
  n이 홀수, F(n) = F(n/2)^2 a

따라서 n이 계속 절반씩 감소하기 때문에 시간복잡도는 O(logN)이다.