[자료구조] 그래프 (1)

10.1 그래프란?

연결되어 있는 객체 간의 관계를 표현하는 자료구조. 많은 문제들은 서로 연결되어 있는 구조로 표현해야 하는데, 선형리스트나 트리의 구조로는 복잡한 문제를 표현할 수 없다. 그래프는 광범위한 분야의 다양한 문제드를 표현해 컴퓨터 프로그램이에 의해 해결할 수 있다.

🌟 트리도 그래프의 특수한 경우(사이클이 없다), 전기회로 소자 간 연결 상태, 지도에서 도시들의 연결 상태

📕오일러

• 오일러 문제: 모든 다리를 한 번만 건너서 처음 출발했던 장소로 돌아오는 문제
• 특정 지역은 정점(node)로, 다리는 간선(Edge)로 표현해 그래프 문제로 변환했다.
• 오일러 경로: 그래프에 존재하는 모든 간선을 한 번만 통과하면서 처음 정점으로 되돌아오는 경로
• 오일러 정리: 모든 정점에 연결된 간선의 수가 짝수이면 오일러 경로가 존재한다.

그래프 ex) 도로망, 선수 과목 관계, 미로

10.2 그래프의 정의와 용어

(1) 용어
그래프 G = (V, E)
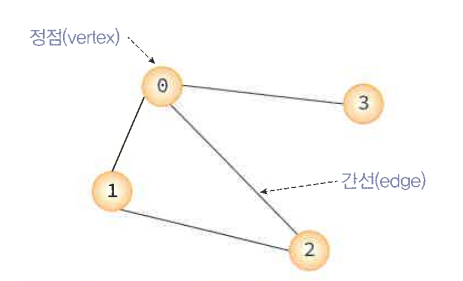
정점 (Vertices) = 노드 (node) = 여러 가지 특성을 가질 수 있는 객체
V(G) = 그래프 G의 정점들의 집합
간선(Edge) = 링크 (link) = 정점들 간의 관계
E(G) = 그래프 G의 간선들의 집합

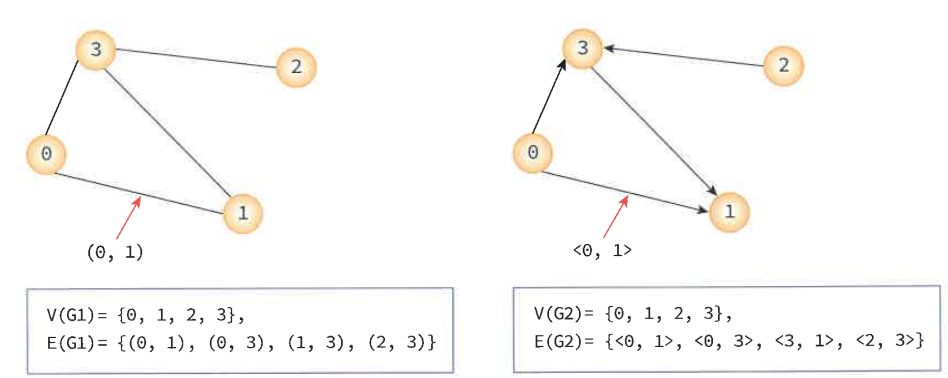
(2) 종류

무방향 그래프, 양방향 그래프

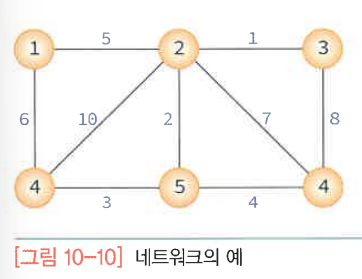
네트워크 = 가중치 그래프 = 간선에 비용이나 가중치가 할당된 그래프
도시를 연결하는 도로의 길이, 회로 소자의 용량, 통신망의 사용료 등을 추가로 표현할 수 있어 응용 분야가 광번위 하다.

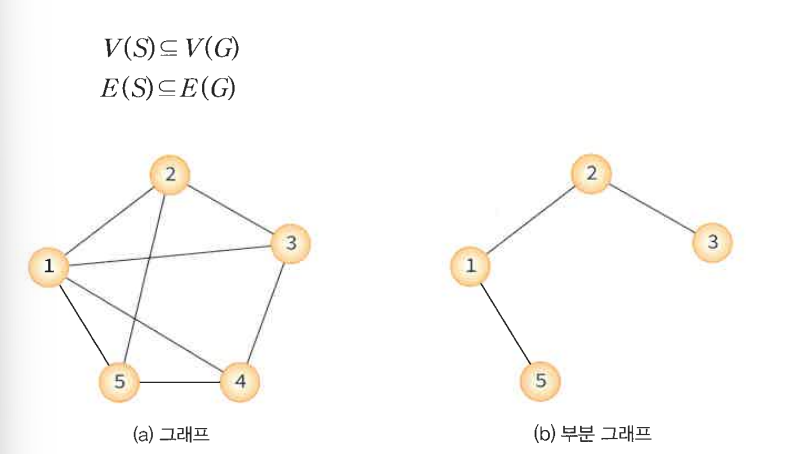
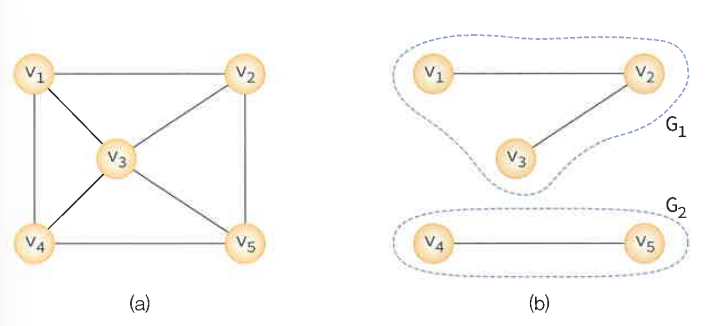
부분 그래프

정점 집합 V(G)와 간선 집합 E(G)의 부분 집합으로 이루어진 그래프

인접 정점(adjacent vertex) = 하나의 정점에서 간선에 의해 직접 연결된 정점

정점의 차수 = 인접 정점의 수
무방향 그래프의 차수 = 간선 수의 두배
방향 그래프의 차수 = 진입 차수, 진출 차수
방향 그래프의 모든 진입(진출) 차수의 합은 간선의 수

경로로 나열된 정점들 간에는 반드시 간선이 존재한다.
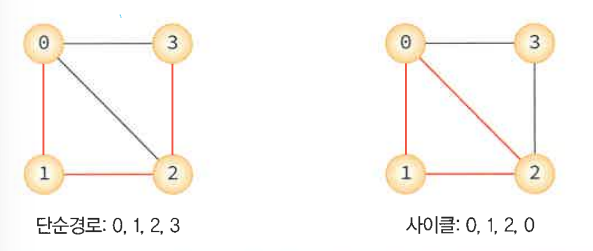
단순 경로는 경로 중에서 반복되는 간선이 없는 경로
사이클은 단순 경로의 시작 정점과 종료 정점이 동일한 경루이다.

연결 그래프
무방향 그래프 G에 있는 모든 정점쌍에 대하여 항상 경로가 존재하는 것. 그렇지 않은 그래프는 비연결 그래프

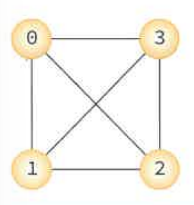
완전 그래프
그래프에 속해있는 모든 정점이 서로 연결되어있는 그래프
n개의 정점을 가진 무방향 완전그래프의 간선의 수 = n(n-1)/2
n=4 => (4*3)/2 = 6

(3) 그래프의 표현 방법

1. 인접 행렬 (Adjacent Matrix)

2차원 배열을 사용해 그래프를 표현한다. 그래프의 정점 수가 n이라면 n*n의 2차원 배열인 인접 행렬 M의 각 원소를 규칙에 의해 할당해 그래프를 메모리에 표현한다.

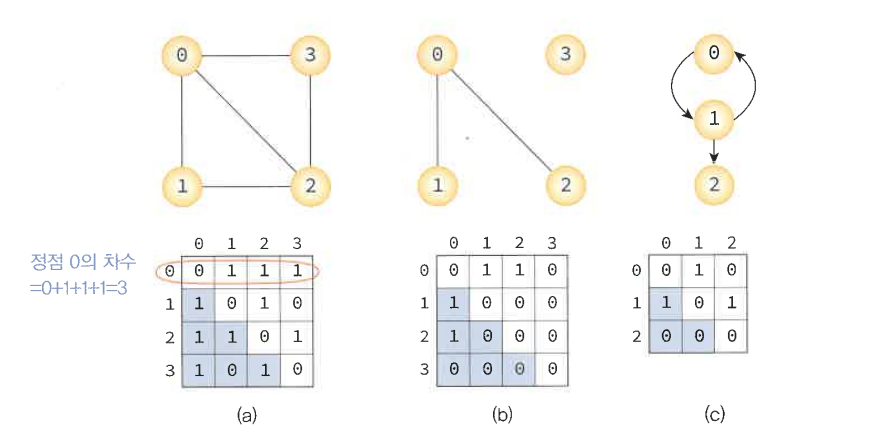
무방향 그래프의 인접 행렬은 대칭이 된다. 간선의 수와 무관하게 항상 n*n의 메모리 공간이 필요하기 때문에, 그래프 내에 적은 숫자의 간선만을 가지는 희소 그래프의 경우에는 메모리 낭비가 크므로 적합하지 않다.

💡인접 행렬을 이용하면 두 정점을 연결하는 간선의 존재 여부를 O(1) 시간 안에 즉시 알 수 있다. 정점의 차수는 인접 행렬의 행이나 열을 조사하면 알 수 있으므로 O(n)의 연산에 의해 알 수 있다. 즉 정점 i에 대한 차수는 인접 배열 i번째 행에 있는 값을 모두 더하면 된다.

💡반면에 그래프에 존재하는 모든 간선의 수를 알아내려면 인접 행렬 전체를 조사해야 하므로 n*n번의 조사가 필요하게 되어 O(n^2)의 시간이 요구된다.

#define N 
typedef struct 
{
	int n; //정점의 개수
    int adjMat[N][N]; //인접 행렬
}GraphType;

한정된 개수의 정점까지만 그래프에 삽입할 수 있다.

#include <stdio.h>
#include <stdlib.h>
#define N 10 //정점의 개수, 인접 배열 사이즈
// #define TRUE 1
// #define FALSE 0 

typedef int element;
int visited[N]; //방문 여부를 조사하는 배열

typedef struct 
{
    int n; // 활성화 시킬 배열의 인덱스 개수
    int adjMat[N][N];
}GraphType;

//그래프 초기화
void initGraph(GraphType *G)
{
    G->n = 0;
    for(int i=0;i<N;i++)
        for(int j=0;j<N;j++)
            G->adjMat[i][j] = 0;
}

//정점 삽입 연산
void makeVertex(GraphType *G)
{
    G -> n ++;
}

void insertEdge(GraphType *G, int u, int v) //간선 삽입 연산
{
    G->adjMat[u][v] = G->adjMat[v][u] = 1; //무방향 그래프니까 U와 V간의 간선이 있으면 V와 U사이도
}

void print(GraphType* G)
{
	for (int i = 1; i <= G->n; i++)
	{
		printf("(");
			for (int j = 1; j <= G->n; j++)
			{
				printf("%d", G->adjMat[i][j]);
			}
			printf(")\n");
	}
}

int main()
{
    GraphType G;
	initGraph(&G);

	int n;
	scanf("%d", &n); //정점의 개수를 입력받는다.

	for (int i = 0; i < n; i++)
		makeVertex(&G);
    
    insertEdge(&G, 1, 2); insertEdge(&G, 1, 3); insertEdge(&G, 1, 5);
	insertEdge(&G, 2, 3); 
	insertEdge(&G, 3, 4); insertEdge(&G, 3, 5);
	insertEdge(&G, 4, 5); print(&G);
}

2. 인접 리스트 (adjacency list)

각각의 정점에 인접한 정점들을 연결 리스트로 표시한 것. 각 연결 리스트의 노드들은 인접 정점을 저장하게 된다. 각 연결 리스트들은 헤더 노드를 가지고 있고 이 헤더 노드들은 하나의 배열로 구성되어있다. 즉, 정점의 번호만 알면 이 번호를 배열의 인덱스로 하여 각 정점의 연결 리스트에 쉽게 접근할 수 있다.

각 연결 리스트에 정점들이 입력되는 순서에 따라 연결 리스트 내에서 정점들의 순서가 달라질 수 있다.

n개의 헤더 노드와 2e개의 노드가 필요하다. 간선의 개수가 적은 희소 그래프의 표현에 적합하다.

💡그래프에 간선 (i, j)의 존재 여부나 정점 i의 차수를 알기 위해서는 인접 리스트에서의 정점 i의 연결 리스트를 탐색해야 하므로, 연결 리스트에 있는 노드의 수만큼의 시간이 필요하다.

=> n개의 정점과 e개의 간선을 가진 그래프에서 전체 간선의 수를 알아내려면 헤더 노드를 포함하여 모든 인접 리스트를 조사해야 하므로 O(n+e)의 연산이 요구된다.

그래프와 관련된 변수 -> GraphType
정점의 개수 n, 포인터 배열, 연결 리스트의 하나의 노드는 GraphNode 구조체로

#include <stdio.h>
#include <stdlib.h>

#define TRUE 1
#define FALSE 0

typedef char element;

typedef struct AdjacentVertex //인접 정점 리스트
{
    element aName; //인접 리스트의 이름
    struct AdjacentVertex* next; 
}AdjacentVertex;

typedef struct Vertex //정점의 연결 리스트
{
    element vName;
    AdjacentVertex* aHead; //인접 정점 리스트를 가리킴
    struct Vertex* next;
}Vertex;

typedef struct
{
    Vertex* vHead;
}GraphType;

void init(GraphType* G)
{
    G->vHead = NULL;
}

void makeVertex(GraphType* G, element vName)
{
    Vertex* v = (Vertex*)malloc(sizeof(Vertex));
    v->vName = vName;
    v->aHead = NULL;
    v->next = NULL;

    Vertex* p = G->vHead;

    if(p==NULL)
        G->vHead = v;
    else
    {
        while(p->next!=NULL)
            p=p->next;
        p->next = v;
    }
}

void makeAdjacentVertex(Vertex *v, element aName)
{
    AdjacentVertex* a = (AdjacentVertex*)malloc(sizeof(AdjacentVertex));
    a->aName = aName;
    a->next = NULL;

    AdjacentVertex* p = v->aHead;

    if(p == NULL)
        v->aHead = a;
    else
    {
        while(p->next!=NULL)
            p=p->next;
        
        p->next = a;
    }
}

Vertex* findVertex(GraphType* G, element vName)
{
    Vertex* p = G->vHead;
    while(p->vName != vName)
        p=p->next;
    
    return p;
}

void insertEdge(GraphType*G, element v1, element v2)
{
    Vertex* v = findVertex(G, v1);
    makeAdjacentVertex(v, v2);

    v = findVertex(G, v2);
    makeAdjacentVertex(v, v1);
}

void print(GraphType *G)
{
    Vertex* p = NULL;
    AdjacentVertex* q = NULL;

    for(p=G->vHead;p!=NULL;p=p->next)
    {
        printf("[%c]: ", p->vName);
        for(q=p->aHead;q!=NULL;q=q->next)
            printf("[%c] ", q->aName);
        
        printf("\n");
    }
}
int main()
{
	GraphType G;
	init(&G);

	//정점이 A~G
	makeVertex(&G, 'a'); makeVertex(&G, 'b');
	makeVertex(&G, 'c'); makeVertex(&G, 'd');
	makeVertex(&G, 'e'); makeVertex(&G, 'f');
	makeVertex(&G, 'g'); //정점 생성 완료
	
	insertEdge(&G, 'a', 'b'); insertEdge(&G, 'a', 'f');//그래프와 정점의 이름. 왼쪽부터 알파벳 순, 간선 추가
	insertEdge(&G, 'b', 'c'); insertEdge(&G, 'b', 'g');
	insertEdge(&G, 'c', 'd');
	insertEdge(&G, 'd', 'e'); insertEdge(&G, 'd', 'g');
	insertEdge(&G, 'e', 'f'); insertEdge(&G, 'e', 'g');
	
	print(&G);

	return 0;
}