[자료구조] 우선순위 큐

9.1 우선순위 큐 추상 데이터 타입

우선순위 큐: 우선순위를 가진 항목들을 저장하는 큐, FIFO순서가 아니라 우선순위가 높은 데이터가 먼저 나가게 된다.
(도로에서 구급차가 먼저 이동하는 걸 생각하자)

💡가장 일반적인 큐: 스택이나 FIFO 큐를 우선순위 큐로 구현할 수 있다. 즉, 스택이나 큐는 우선순위 큐의 부분집합이다. (적절한 우선순위를 설정하면 우선순위 큐는 스택이나 큐로 동작할 것이다.)

• 스택 - 우선순위 = 최신
• 큐 - 우선순위 = 최초
• 우선순위큐 - 가장 우선순위가 높은 데이터

🖥️ 응용분야: 네트워크 트래픽 제어, 운영 체제에서의 작업 스케줄링 등, 시뮬레이션 시스템

insert, delete 연산이 중요. 최소 우선순위 큐는 가장 우선순위가 낮은 요소를 먼저 삭제하고, 최대 우선순위 큐는 우선순위가 가장 높은 요소가 먼저 삭제된다.

(1) 우선순위 큐 구현 방법

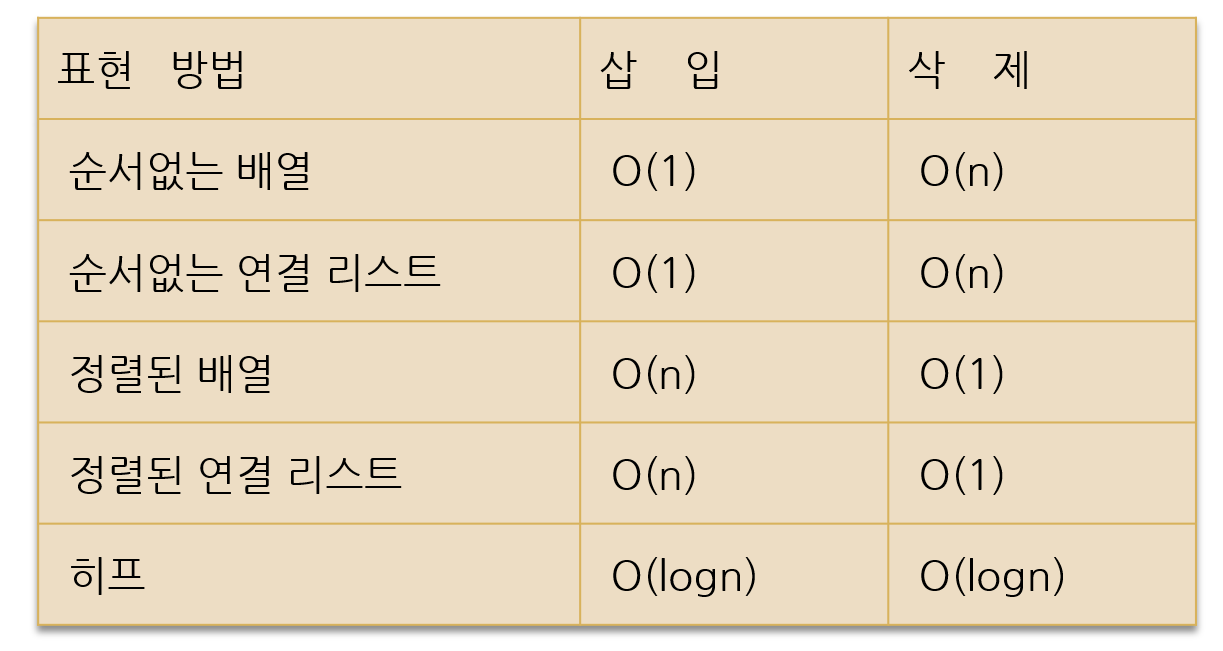
💡정렬이 되어있지 않으면, 그냥 맨끝에 요소를 추가하면 되기 때문에 시간 복잡도는 O(1)이다. 삭제를 할 때는 가장 우선순위가 높은 요소를 찾아야 하는데, 정렬이 되어있지 않기 때문에 모든 요소를 탐색해야해서 O(n)이 된다.
💡정렬이 되어있다면, 다른 요소와 값을 비교해 삽입 위치를 찾아야 하기 때문에 순차탐색이나 이진탐색과 같은 방법을 이용한다. 그 다음 요소를 이동시켜 빈자리를 만든다음 삽잉ㅂ한다. 삭제시에는 맨 뒤만 삭제하면 된다.

(2) 히프

📕히프 Heap란?
노드의 키들이 부모노드의 키 >= 자식노드의 키를 만족하는 완전 이진 트리. (h-1 레벨 까지는 포화이진트리, h레벨은 맨 왼쪽부터 순서대로 집어넣는다.)

• 최대 히프: 부모 노드의 키값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
  

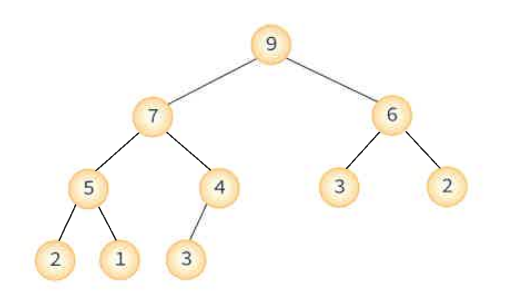
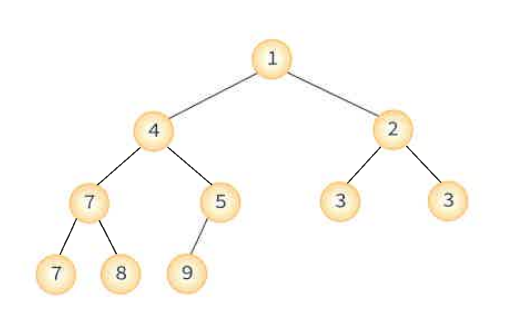
• 최소 히프: 부모 노드의 키 값이 자식 노드의 키값보다 작거나 같은 완전 이진 트리
  

(3) 히프의 구현

히프는 완전 이진 트리이기 때문에 각각의 노드에 차례대로 번호를 붙일 수 있다. 이 번호를 배열의 인덱스로 생각하면 배열에 히프의 노드들을 저장할 수 있다.

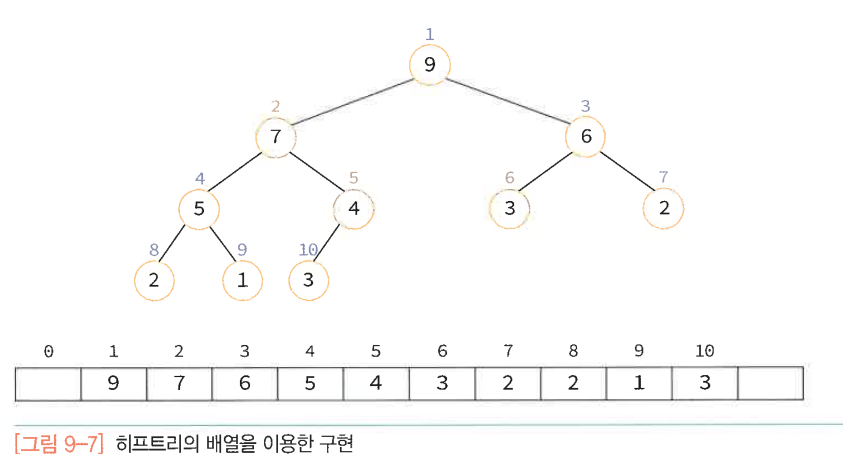
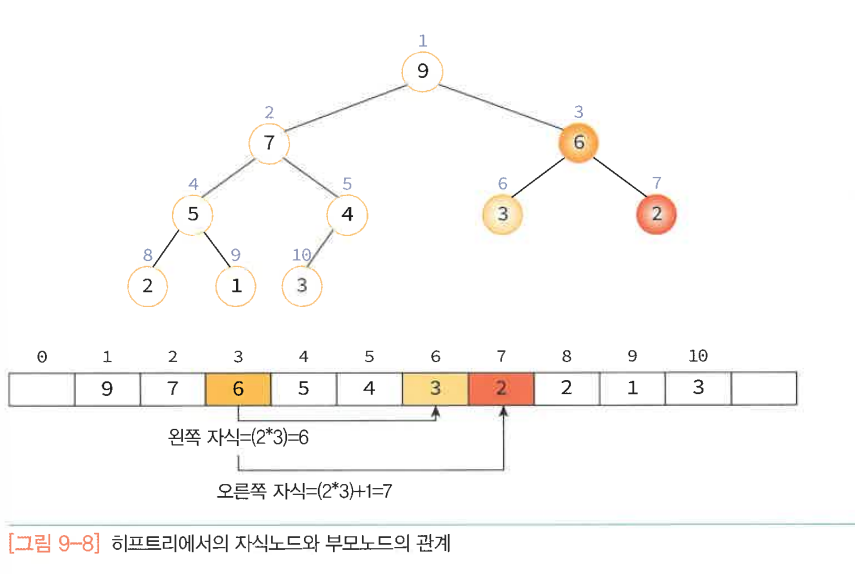
부모의 인덱스 = 자식의 인덱스/2

(3-1) 히프의 정의

1차원 배열을 만들어 히프를 구현한다.

#include <stdio.h>
#include <stdlib.h>

#define N 100

typedef int element;

typedef struct
{
    element heap[N]; //heap을 배열로
    int heapSize; //stack에서의 top과 같은 역할, 마지막 데이터의 인덱스를 가리킬 것임
}HeapType;

(3-2) 히프의 삽입 연산

우선순위에 따른 값을 빨리 찾아야 하는 경우

1. 히프에 새로운 요소가 들어오면, 일단 새로운 노드를 히프의 마지막 노드에 이어서 삽입한다.
2. 삽입 후에 새로운 노드를 부모 노드들과 교환해서 히프의 성질을 만족한다. 우선순위에 따라 바꾸는 것이다.

히프의 정의

#define N 100

typedef int element;

typedef struct
{
    element heap[N]; //heap을 배열로
    int heapSize; //stack에서의 top과 같은 역할, 마지막 데이터의 인덱스를 가리킬 것임
}HeapType;

upheap 연산

void upheap(HeapType* H)
{
    int i = H->heapSize;
    element key = H->heap[i];
    
    //내 부모가 있는지 확인해야 함.
    while((i != 1) && (key > H -> heap[i/2])) //i가 루트가 아니고, 부모 노드의 값보다 key값이 크면
    {
        H -> heap[i] = H -> heap[i/2]; //부모노드의 값을 삽입하려는 위치에 넣는다
        i/=2;
    }
    
    H->heap[i] = key; //원래 부모노드의 자리에 key값이 들어간다.
}

void InsertHeap(HeapType* H, int key)
{
    H->heapSize++; 
    H->heap[H->heapSize] = key; //새 노드 삽입
    upheap(H); //재구성
}

(3-2) 히프의 삭제 연산

최대 히프에서의 삭제는 가장 큰 키 값을 가진 노드를 삭제하는 것. 즉, 루트 노드가 삭제된다. 삭제 후 히프의 성질을 만족하기 위해 위, 아래 노드를 교환하는 재구성을 한다.

1. 루트 노드를 삭제한다
2. 마지막 노드를 루트 노드로 이동한다.
3. 루트에서부터 단말 노드까지의 경로에 있는 노드들을 교환하여 히프 성질을 만족시킨다.

void downHeap(HeapType* H)
{
    element key = H->heap[1];
    int parent = 1, child = 2;
    //내 위치에서 자식노드가 있는 동안 downHeap
    
    while(child <= H->heapSize) //downHeap을 할 수 있는 범위 안에 있네, child 가 마지막 노드이다.
    {
        if((child < H->heapSize) && (H->heap[child+1] > H->heap[child])) //child는 오른쪽 형제 노드를 최소한 한 개 가지고 있다.  
            child++;
        if(key >= H->heap[child])
            break; //한 단계 아래로 이동
        H->heap[parent] = H->heap[child];
        parent = child;
        child *= 2;
    }
    H->heap[parent] = key;
}

element removeHeap(HeapType* H)
{
    element key = H -> heap[1]; //루트 노드.
    
    H->heap[1] = H->heap[H->heapSize]; //말단 노드를 루트 노드로 옮김
    H->heapSize--;
    downHeap(H); //루트의 자식과 비교 시작, 재구성
    
    return key; 
}

전체코드

#include <stdio.h>
#include <stdlib.h>

#define N 100

typedef int element;

typedef struct
{
    element heap[N]; //heap을 배열로
    int heapSize; //stack에서의 top과 같은 역할, 마지막 데이터의 인덱스를 가리킬 것임
}HeapType;

void init(HeapType *H)
{
    H->heapSize = 0;
}

//현재 요소의 개수가 heapSize인 히프 H에 삽입한다.
void upheap(HeapType* H)
{
    int i = H->heapSize;
    element key = H->heap[i];
    
    //내 부모가 있는지 확인해야 함.
    while((i != 1) && (key > H -> heap[i/2])) //i가 루트가 아니고, 부모 노드의 값보다 key값이 크면
    {
        H -> heap[i] = H -> heap[i/2]; //부모노드의 값을 삽입하려는 위치에 넣는다
        i/=2;
    }
    
    H->heap[i] = key; //원래 부모노드의 자리에 key값이 들어간다.
}

void downHeap(HeapType* H)
{
    element key = H->heap[1];
    int parent = 1, child = 2;
    //내 위치에서 자식노드가 있는 동안 downHeap
    
    while(child <= H->heapSize) //downHeap을 할 수 있는 범위 안에 있네, child 가 마지막 노드이다.
    {
        if((child < H->heapSize) && (H->heap[child+1] > H->heap[child])) //child는 오른쪽 형제 노드를 최소한 한 개 가지고 있다.  
            child++;
        if(key >= H->heap[child])
            break; //한 단계 아래로 이동
        H->heap[parent] = H->heap[child];
        parent = child;
        child *= 2;
    }
    H->heap[parent] = key;
}

void InsertHeap(HeapType* H, int key)
{
    H->heapSize++;
    H->heap[H->heapSize] = key;
    upheap(H);
}

element removeHeap(HeapType* H)
{
    element key = H -> heap[1]; //루트 노드.
    
    H->heap[1] = H->heap[H->heapSize]; //말단 노드를 루트 노드로 옮김
    H->heapSize--;
    downHeap(H); //루트의 자식과 비교 시작, 재구성
    
    return key; 
}

void print(HeapType* H)
{
    for(int i=1;i<=H->heapSize;i++)
        printf("[%d] ", H->heap[i]);
    printf("\n");
}
int main()
{
    HeapType H;
    init(&H);
    
    InsertHeap(&H, 9); InsertHeap(&H, 7); InsertHeap(&H, 6);
    InsertHeap(&H, 5); InsertHeap(&H, 4); InsertHeap(&H, 3);
    InsertHeap(&H, 2); InsertHeap(&H, 2); InsertHeap(&H, 1);
    InsertHeap(&H, 3); 
    
    print(&H);
    
    removeHeap(&H); print(&H);
    removeHeap(&H); print(&H);
    //InsertHeap(&H, 8); print(&H);
    return 0;
}

(4) 히프의 복잡도 분석

🌟삽입 연산에서 새로운 요소 히프트리를 타고 올라가면서 부모 노드들과 교환을 하게 되는데, 최악의 경우, 루트 노드까지 올라가야 하므로 거의 트리의 높이에 해당하는 비교 연산 및 이동 연산이 필요하다. 히프가 완전 이진트리임을 생각하면 히프의 높이는 log2n이 되고 따라서 삽입의 시간복잡도는 O(log2n)

🌟삭제도 마찬가지로 마지막 노드를 루트로 가져온 후에 자식 노드들과 비교하여 교환하는 부분이 가장 오래걸리므로, 최악의 경우 가장 아래 레벨까지 내려가야 하므로 트리의 높이만큼의 시간이 걸린다. 따라서 삭제의 시간복잡도도 O(log2n)이 된다.

(5) Heap 정렬

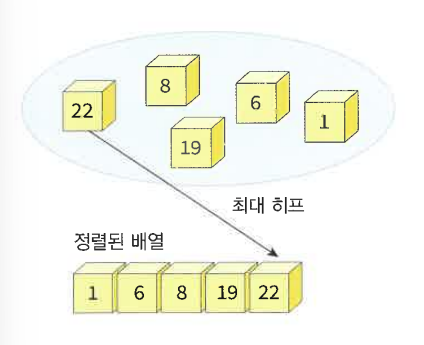
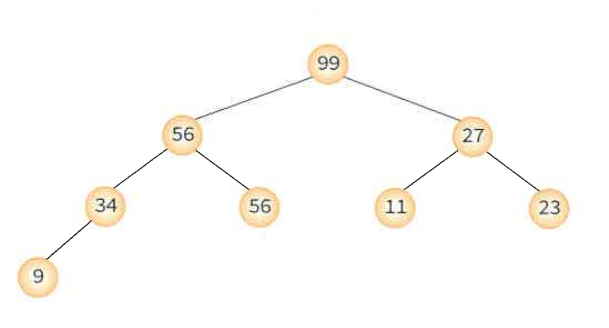
최대 히프를 이용하면 정렬할 수 있다.
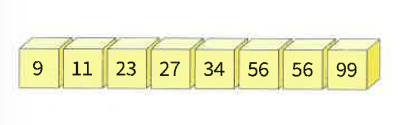
정렬해야 할 n개의 요소를 최대 히프에 삽입하고, 한번에 하나씩 요소를 히프에서 삭제하여 저장한다. 삭제되는 요소들은 값이 증가되는 순서이다(최소히프의 경우).
하나의 요소를 히프에 삭제하거나 삽입할때는 o(log2n)이 걸리고, 삽입되는 요소의 개수가 n개이므로 전체적으로 O(nlogn)의 시간이 걸린다.

🌟히프 정렬이 최대로 유용한 경우는 전체 자료를 정렬하는 것이 아니라, 가장 큰 값 몇 개만 필요할 때다.

void heapSort(HeapType* H)
{
    int n = H->heapSize;
    element A[n]; //별도의 배열을 생성한 것임. 이렇게 말고  H->heap[] 배열에 바로 정렬 시키기. 제자리 정렬
    
    for(int i = n-1 ; i >=0 ; i--)
        A[i] = removeHeap(H);
        
    for(int i=0;i <n;i++)
        printf("[%d] ", A[i]);
    printf("\n");
}