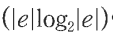- 최소 비용 신장 트리 (Minimum spanning tree)
신장 트리(spanning tree): 그래프 내의 모든 정점을 포함하는 트리. 사이클을 포함해서는 안되고 n개의 정점을 가지는 그래프의 신장 트리는 n-1개의 간선을 가진다. MST는 신장 트리 중에서 사용된 간선들의 가중치 합이 최소인 신장트리다.
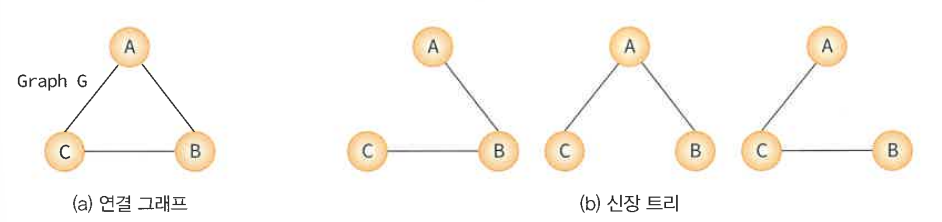
신장 트리는 그래프의 최소 연결 부분 그래프가 된다. 네트워크 구축에 많이 사용된다. 단순히 가장 적은 링크만이 아닌, 간선에 비용을 붙여서 링크의 구축 비용까지를 고려해 최소 비용의 신장 트리를 선택할 필요가 있다.
ex) 도로 건설(길이 최소), 전기 회로(전선 길이 최소), 통신(전화선 길이 최소), 배관(파이프의 총 길이 최소)
//간선의 가중치를 부여해 출력하는 코드
#include <stdio.h>
#include <stdlib.h>
#define TRUE 1
#define FALSE 0
#define N 10
typedef char element;
typedef struct Edge
{
element v1, v2;
int weight; //가중치
struct Edge* next; //연결리스트 표현 위해서
}Edge;
typedef struct AdjacentVertex //빨간색 리스트의 관리의 주체는 각각의 Vertex
{
element aName; //인접 정점 리스트의 이름
Edge* e; //헤더역할이 아님, 엣지를 가리키게 하는 역할. (aHead, Vhead와는 역할이 다름, 하나의 간선을 가리키는 포인터)
struct AdjacentVertex* next;
}AdjacentVertex;
typedef struct Vertex //단순 연결 리스트, 정점의 연결 리스트, 까만색 리스트의 관리의 주체는 그래프
{
element vName;
//각각의 Vertex는 첫번째 인접 정점 adjacentvertex 노드를 가르키는, aHead를 갖게 한다.
//visited 배열을 사용할 필요 없이, 방문 여부를 검사하는 필드를 추가한다 => isVisit
int isVisit;
AdjacentVertex* aHead;
struct Vertex* next;
}Vertex;
typedef struct //간선은 그래프가 관리, 정점 뿐만 아니라 간선까지
{
Vertex* vhead;
Edge* eHead;
int vCount, eCount;
}GraphType;
//최단 경우 알고리즘의 경우, 그래프에서 트리로 만들어질 때의 조건(정점의 개수 - 1개의 간선을 찾는것)
//간선의 개수를 기억하고 있어야 함
void init(GraphType* G)
{
G->vhead = NULL;
G->eHead = NULL;
G->vCount = G->eCount = 0;
}
void makeVertex(GraphType* G, element vName) //insertLast
{
Vertex* v = (Vertex*)malloc(sizeof(Vertex)); //정점
v->vName = vName;
v->aHead = NULL; //정점이 만들어 졌을 때 나와 연결된 정점은 아직 없음.
v->isVisit = FALSE; //방문하지 않았다.
v->next = NULL; //여기까지는 정점이 하나 만들어졌다. vCount가 증가 된다.
G->vCount++;
//자기 자리까지 찾아주기
Vertex* p = G->vhead;
if (p == NULL) //다 비어있는 상태, 초기상태이면, 현재로서 첫번째 노드라면
G->vhead = v; //나를 가르켜야한다.
else
{
while (p->next != NULL)
p = p->next;
p->next = v;
}
}
void makeAdjacentVertex(Vertex* v, element aName, Edge* e) //aName = 인접 정점의 이름
{
AdjacentVertex* a = (AdjacentVertex*)malloc(sizeof(AdjacentVertex));
a->aName = aName;
a->e = e;
a->next = NULL; //insertLast
AdjacentVertex* p = v->aHead; //각각의 관리자는 vertex니까 G대신 v가 넘어옴
if (p == NULL)
v->aHead = a;
else
{
while (p->next != NULL)
p = p->next;
p->next = a;
}
}
Vertex* findVertex(GraphType* G, element vName) //정점의 이름으로 정점 객체 찾는 함수. 기억하기
{
Vertex* p = G->vhead;
while (p->vName != vName)
p = p->next;
return p;
}
void insertEdge(GraphType* G, element v1, element v2, int weight)
{
Edge* e = (Edge*)malloc(sizeof(Edge)); //간선 노드를 생성
e->v1 = v1;
e->v2 = v2;
e->weight = weight;
e->next = NULL; //간선의 다음 간선은 insertlast니까 NULL
G->eCount++;
Edge* p = G->eHead; //화살표, 그래프를 가리키는 첫번째 간선
if (p == NULL) //간선이 하나도 없는 경우, 그래프의 첫번째 간선일 경우
G->eHead = e;
else
{
while (p->next != NULL)
p = p->next;
p->next = e;
}
Vertex* v = findVertex(G, v1);
makeAdjacentVertex(v, v2, e); //누가 정점과 간선을 연결해줬는지 전달해줘야함 (e)
v = findVertex(G, v2);
makeAdjacentVertex(v, v1, e);
}
void print(GraphType* G)
{
Vertex* p = NULL;
AdjacentVertex* q = NULL;
for (p = G->vhead; p != NULL; p = p->next)
{
printf("[%c] : ", p->vName);
for (q = p->aHead; q != NULL; q = q->next) //현재 정점의 인접 정점 리스트의 첫 노드를 가리키고
{
printf("[%c, %d] ", q->aName, q->e->weight); //q->e는 초록색 화살표, 따라가면 간선이 나옴
}
printf("\n");
}
}
int main()
{
GraphType G;
init(&G);
//정점이 A~G
makeVertex(&G, 'a'); makeVertex(&G, 'b');
makeVertex(&G, 'c'); makeVertex(&G, 'd');
makeVertex(&G, 'e'); makeVertex(&G, 'f');
makeVertex(&G, 'g'); //정점 생성 완료
insertEdge(&G, 'a', 'b', 29); insertEdge(&G, 'a', 'f', 10);//그래프와 정점의 이름. 왼쪽부터 알파벳 순, 간선 추가
insertEdge(&G, 'b', 'c', 16); insertEdge(&G, 'b', 'g', 15);
insertEdge(&G, 'c', 'd', 12);
insertEdge(&G, 'd', 'e', 22); insertEdge(&G, 'd', 'g', 18);
insertEdge(&G, 'e', 'f', 27); insertEdge(&G, 'e', 'g', 25);
print(&G);
return 0;
}- Kruskal의 MST 알고리즘
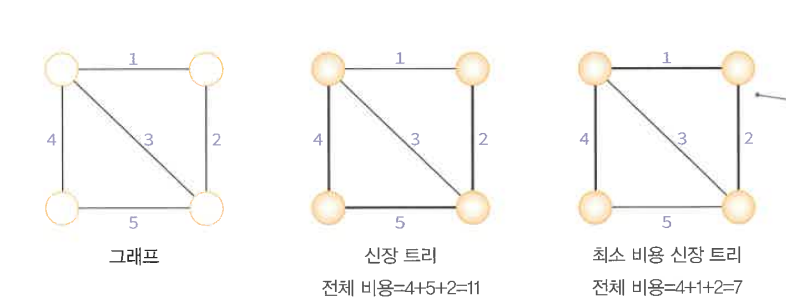
탐욕적인 방법, 각 단계에서 최선의 답을 선택하는 과정을 반복함으로써 최종적인 해답에 도달하는 방법. 순간의 선택은 그 당시에는 최적이나, 그 해답을 모은 최종적인 해답이 전역적으로 치적이라는 보장은 없다. kruskal은 최적의 해답을 준다.
=> 정점에서 뻗어나가면서 연결, 트리가 확장되면서 MST를 찾는 형태
Kruskal 알고리즘은 MST가 최소 비용의 간선으로 구성됨과 도잇에 사이클을 포함하지 않는 조건에 근거하여, 각 단계에서 사이클을 이루지 않는 최소 비용 간선을 선택한다.
(1) 그래프의 간선들을 가중치의 오름차순으로 정렬한다.
(2) 정렬된 간선들의 리스트에서 사이클을 형성하지 않는 간선을 찾아서 현재의 최소 비용 신장 트리의 집합에 추가한다.
(3) 사이클을 형성하면 그 간선은 제외된다.
💡 새로운 간선이 이미 다른 경로에 의하여 연결되어 있는 정점들을 연결하는지 체크, 추가하고자 하는 간선의 양끝 정점이 같은 집합에 속해 있는지 먼저 검사한다.
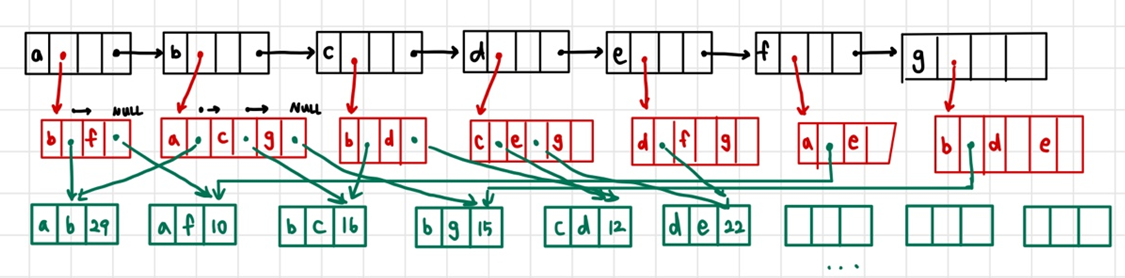
- union-find 알고리즘
원소가 어떤 집합에 속하는 지 알아낸다. 트리 형태를 사용하며, 부모 노드만 알면 되므로 부모 포인터 표현을 사용한다. (노드에 대해 노드의 부모에 대한 포인터만 저장)
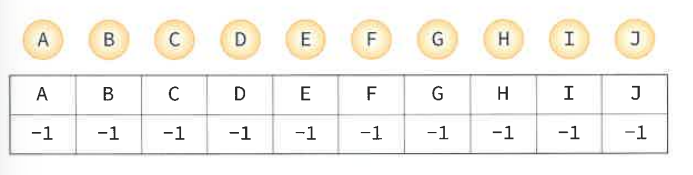
1차원 배열로 구현, -1은 부모 노드가 없는 상태
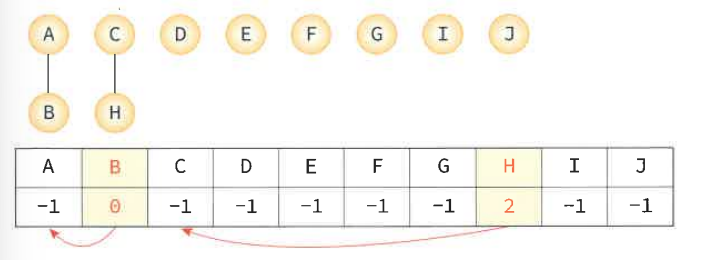
union(a,b) union(c,h)
#include <stdio.h>
#include <stdlib.h>
#define TRUE 1
#define FALSE 0
#define N 10
typedef char element;
typedef struct Edge
{
element v1, v2;
int weight; //가중치
struct Edge* next; //연결리스트 표현 위해서
}Edge;
typedef struct AdjacentVertex //빨간색 리스트의 관리의 주체는 각각의 Vertex
{
element aName; //인접 정점 리스트의 이름
Edge* e; //헤더역할이 아님, 엣지를 가리키게 하는 역할. (aHead, Vhead와는 역할이 다름, 하나의 간선을 가리키는 포인터)
struct AdjacentVertex* next;
}AdjacentVertex;
typedef struct Vertex //단순 연결 리스트, 정점의 연결 리스트, 까만색 리스트의 관리의 주체는 그래프
{
element vName;
//각각의 Vertex는 첫번째 인접 정점 adjacentvertex 노드를 가르키는, aHead를 갖게 한다.
//visited 배열을 사용할 필요 없이, 방문 여부를 검사하는 필드를 추가한다 => isVisit
int isVisit;
AdjacentVertex* aHead;
struct Vertex* next;
}Vertex;
typedef struct //간선은 그래프가 관리, 정점 뿐만 아니라 간선까지
{
Vertex* vhead;
Edge* eHead;
int vCount, eCount;
}GraphType;
//최단 경우 알고리즘의 경우, 그래프에서 트리로 만들어질 때의 조건(정점의 개수 - 1개의 간선을 찾는것)
//간선의 개수를 기억하고 있어야 함
void init(GraphType* G)
{
G->vhead = NULL;
G->eHead = NULL;
G->vCount = G->eCount = 0;
}
void makeVertex(GraphType* G, element vName) //insertLast
{
Vertex* v = (Vertex*)malloc(sizeof(Vertex)); //정점
v->vName = vName;
v->aHead = NULL; //정점이 만들어 졌을 때 나와 연결된 정점은 아직 없음.
v->isVisit = FALSE; //방문하지 않았다.
v->next = NULL; //여기까지는 정점이 하나 만들어졌다. vCount가 증가 된다.
G->vCount++;
//자기 자리까지 찾아주기
Vertex* p = G->vhead;
if (p == NULL) //다 비어있는 상태, 초기상태이면, 현재로서 첫번째 노드라면
G->vhead = v; //나를 가르켜야한다.
else
{
while (p->next != NULL)
p = p->next;
p->next = v;
}
}
void makeAdjacentVertex(Vertex* v, element aName, Edge* e) //aName = 인접 정점의 이름
{
AdjacentVertex* a = (AdjacentVertex*)malloc(sizeof(AdjacentVertex));
a->aName = aName;
a->e = e;
a->next = NULL; //insertLast
AdjacentVertex* p = v->aHead; //각각의 관리자는 vertex니까 G대신 v가 넘어옴
if (p == NULL)
v->aHead = a;
else
{
while (p->next != NULL)
p = p->next;
p->next = a;
}
}
Vertex* findVertex(GraphType* G, element vName) //정점의 이름으로 정점 객체 찾는 함수. 기억하기
{
Vertex* p = G->vhead;
while (p->vName != vName)
p = p->next;
return p;
}
void insertEdge(GraphType* G, element v1, element v2, int weight)
{
Edge* e = (Edge*)malloc(sizeof(Edge)); //간선 노드를 생성
e->v1 = v1;
e->v2 = v2;
e->weight = weight;
e->next = NULL; //간선의 다음 간선은 insertlast니까 NULL
G->eCount++;
Edge* p = G->eHead; //화살표, 그래프를 가리키는 첫번째 간선
if (p == NULL) //간선이 하나도 없는 경우, 그래프의 첫번째 간선일 경우
G->eHead = e;
else
{
while (p->next != NULL)
p = p->next;
p->next = e;
}
Vertex* v = findVertex(G, v1);
makeAdjacentVertex(v, v2, e); //누가 정점과 간선을 연결해줬는지 전달해줘야함 (e)
v = findVertex(G, v2);
makeAdjacentVertex(v, v1, e);
}
void print(GraphType* G)
{
Vertex* p = NULL;
AdjacentVertex* q = NULL;
for (p = G->vhead; p != NULL; p = p->next)
{
printf("[%c] : ", p->vName);
for (q = p->aHead; q != NULL; q = q->next) //현재 정점의 인접 정점 리스트의 첫 노드를 가리키고
{
printf("[%c, %d] ", q->aName, q->e->weight); //q->e는 초록색 화살표, 따라가면 간선이 나옴
}
printf("\n");
}
}
void incSort(GraphType* G, Edge* edges[])
{
int i, least; //i는 outerloop, least는 매 단계 범위가 줄어들때, 전체 범위에서 젤 범위가 작은것을 기억하는 변수
Edge* p = G->eHead; //그래프의 간선 연결리스트에서 순서대로 방문할 화살표
for (i = 0; i < G->eCount; i++)
{
edges[i] = p; //순서대로간선 주소를 집어넣음
p = p->next;
}
for (i = 0; i < G->eCount - 1; i++) //i는 7번까지 돌고 (0~7), i가 7번까지만 가면 j가 8로 가서 마지막 두개를 비교할 수 있다
{
least = i;
for (int j = i + 1; j < G->eCount; j++) //j는 8번까지 돌음 (1~8)
{
if (edges[j]->weight < edges[least]->weight) //배열 안에 있는건 간선 구조체 포인터, weight에 접근하려면 ->.
least = j;
}
p = edges[least];
edges[least] = edges[i];
edges[i] = p;
}
for (i = 0; i < G->eCount; i++)
printf("[%c%c%d] ", edges[i]->v1, edges[i]->v2, edges[i]->weight);
printf("\n");
}
int vFind(int vertices[], int vNum)
{
if (vertices[vNum] == -1) //속해있는 집합이 없으면
return vNum; //리턴된 인덱스의 값이 다르면 서로 다른집합임
while (vertices[vNum] != -1)
vNum = vertices[vNum];
return vNum;
}
void vUnion(int vertices[], int vNum1, int vNum2)
{
vertices[vNum2] = vNum1; //5번 인덱스에 0을 집어넣는다.
}
void kruskal(GraphType* G, Edge* edges[], int vertices[])
{
int eCnt = 0, i = 0; //k대신에 i 사용
int vNum1, vNum2; //정점의 이름, 숫자 타입으로 바꿔줄려고
Edge* e; //끄집어 낼 간선 포인터
while (eCnt < G->vCount - 1) //전체 정점의 개수 -1개의 간선 개수만큼 반복됨
{
//이미 정렬이 되어 있는상태의 간선
e = edges[i]; //af10이 날라옴, 가중치가 제일 작았으니까
//이제 정점 a와 f의 집합을 찾음 vfind가 각 집합을 찾아
vNum1 = vFind(vertices, e->v1 - 97); //v1이 a, v2가 f, 집합 번호 리턴, e->v1이 알파벳이여서 숫자로 변환
vNum2 = vFind(vertices, e->v2 - 97); //서로 다른집합일 때 유니온
if (vNum1 != vNum2)
{
eCnt++;
//간선을 추가하는 건 화면에 출력하는 방식으로
printf("%d, [%c%c %d]\n", eCnt, e->v1, e->v2, e->weight);
//같은 집합으로 만들어줌
vUnion(vertices, vNum1, vNum2);
}
i++;
}
}
int main()
{
GraphType G;
init(&G);
//정점이 A~G
makeVertex(&G, 'a'); makeVertex(&G, 'b');
makeVertex(&G, 'c'); makeVertex(&G, 'd');
makeVertex(&G, 'e'); makeVertex(&G, 'f');
makeVertex(&G, 'g'); //정점 생성 완료
insertEdge(&G, 'a', 'b', 29); insertEdge(&G, 'a', 'f', 10);//그래프와 정점의 이름. 왼쪽부터 알파벳 순, 간선 추가
insertEdge(&G, 'b', 'c', 16); insertEdge(&G, 'b', 'g', 15);
insertEdge(&G, 'c', 'd', 12);
insertEdge(&G, 'd', 'e', 22); insertEdge(&G, 'd', 'g', 18);
insertEdge(&G, 'e', 'f', 27); insertEdge(&G, 'e', 'g', 25);
print(&G);
//간선 주소들의 배열 생성
Edge* edges[N];
printf("\n");
incSort(&G, edges); //오름차순 배열
int vertices[N] = { -1, -1, -1, -1, -1, -1, -1, -1, -1, -1 }; //unionFind 위해 사용하는 배열
kruskal(&G, edges, vertices); //정렬된 간선배열과 -1로 초기화 되어있는 vertices 정점 관련 배열 전달
return 0;
}시간복잡도 분석
kruskal의 알고리즘의 시간복잡도는 간선들을 정렬하는 시간에 좌우된다. 따라서 효율적인 정렬 알고리즘을 사용한다면 Kruskal의 알고리즘의 시간 복잡도는