- Prim의 MST 알고리즘
시작 정점에서 출발하여 신장 트리 집합을 단계적으로 확장해나가는 방법.
신장 트리 집합에 인접한 정점 중에서 최저 간선으로 연결된 정점을 선택해 신장 트리 집합에 추가한다.
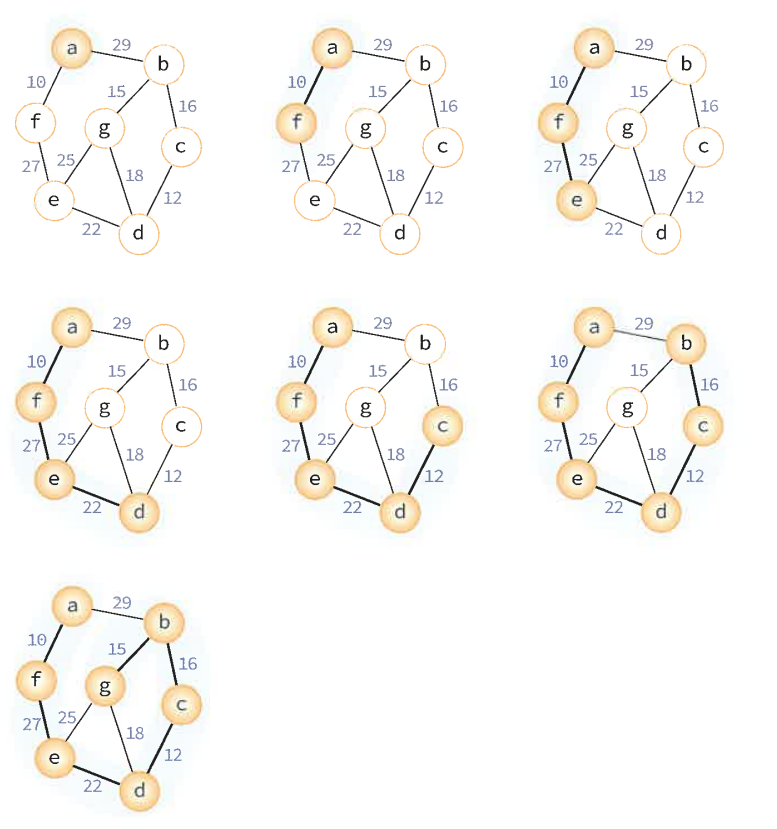
신장 트리 집합에 정점의 개수가 n-1개가 될 때 까지 반복한다.
💡 Kruskal의 알고리즘은 간선 기반인 반면 Prim의 알고리즘은 정점을 기반으로 하는 알고리즘이다. 또한 kruskal은 이전 단계에서 만들어진 신장 트리와는 상관없이 무조건 최저 간선만을 선택하는 방법이지만 Prim의 알고리즘은 이전 단계에서 만들어진 신장 트리를 확장하는 방식이다.
🖥️ 알고리즘
(1) distance[] = 정점의 개수 크기의 배열, 신장 트리 정점 집합에서 각 정점까지의 거리를 가지고 있다. 처음에 시작 정점 노드의 값만이 0이고 다른 노드는 전부 무한대의 값을 가진다.
(2) 트리 집합에 새로운 정점 u가 추가되면, u에 인접한 정점 v들의 distance 값을 변경시켜준다. distance[v]의 값보다 간선 (u,v)의 가중치 값이 적으면 변경한다
(3) Q에 있는 모든 정점들이 소진될 때 까지 되풀이한다.
#include <stdio.h>
#include <stdlib.h>
#define TRUE 1
#define FALSE 0
#define N 20
#define INF 100
int dist[N];
typedef char element;
typedef struct Edge
{
element v1, v2;
int weight;
struct Edge* next;
}Edge;
typedef struct AdjacentVertex
{
element aName;
struct AdjacentVertex* next;
Edge* e;
}AdjacentVertex;
typedef struct Vertex
{
element vName;
int isvisit;
struct Vertex* next;
AdjacentVertex* aHead;
}Vertex;
typedef struct
{
Vertex* vHead;
Edge* eHead;
int vCount, eCount;
}GraphType;
void init(GraphType* G)
{
G->vHead = NULL;
G->eHead = NULL;
G->eCount = G->vCount = 0;
for(int i=0 ; i<N ; i++)
dist[i] = INF;
}
void makeVertex(GraphType* G, element vName)
{
Vertex* v = (Vertex*)malloc(sizeof(Vertex));
v->vName = vName;
v->isvisit = FALSE;
v->next = NULL;
v->aHead = NULL;
G->vCount++;
Vertex* p = G->vHead;
if(p==NULL)
G->vHead = v;
else
{
while(p->next != NULL)
p=p->next;
p->next = v;
}
}
void makeAdjacentVertex(Vertex* v, element aName, Edge* e)
{
AdjacentVertex* a = (AdjacentVertex*)malloc(sizeof(AdjacentVertex));
a->aName = aName;
a->next = NULL;
a->e = e;
AdjacentVertex* p = v->aHead;
if(p == NULL)
v->aHead = a;
else
{
while(p->next != NULL)
p=p->next;
p->next = a;
}
}
Vertex* findVertex(GraphType* G, element vName)
{
Vertex* p = G->vHead;
while(p->vName != vName)
p=p->next;
return p;
}
void insertEdge(GraphType *G, element v1, element v2, int weight)
{
Edge* e = (Edge*)malloc(sizeof(Edge));
e->v1 = v1;
e->v2 = v2;
e->next = NULL;
e->weight = weight;
G->eCount++;
Edge* p = G->eHead;
if(p==NULL)
G->eHead = e;
else
{
while(p->next != NULL)
p=p->next;
p->next = e;
}
Vertex* v = findVertex(G, v1);
makeAdjacentVertex(v, v2, e);
v = findVertex(G, v2);
makeAdjacentVertex(v, v1, e);
}
void print(GraphType* G)
{
Vertex* p = NULL;
AdjacentVertex* q = NULL;
for(p=G->vHead;p!=NULL;p=p->next)
{
printf("[%c] : ", p->vName);
for(q=p->aHead;q!=NULL;q=q->next)
printf("[%c, %d]", q->aName, q->e->weight);
printf("\n");
}
}
element getMinVertex(GraphType* G)
{
Vertex* v = NULL;
element minName;
for(v=G->vHead;v!=NULL;v=v->next)
{
if(v->isvisit == FALSE)
{
minName = v->vName;
break;
}
}
for(v=G->vHead; v!=NULL ; v=v->next)
if((v->isvisit == FALSE) && dist[v->vName-97]<dist[minName-97])
minName = v->vName;
return minName;
}
void prim(GraphType* G, element vName)
{
Vertex* v =NULL;
AdjacentVertex* a = NULL;
element minName;
dist[vName-97] = 0;
for(int i=0;i<G->vCount;i++)
{
minName = getMinVertex(G);
v=findVertex(G, minName);
v->isvisit = TRUE;
printf("[%c] ", v->vName);
for(a=v->aHead;a!=NULL;a=a->next)
{
v=findVertex(G, a->aName);
if(v->isvisit==FALSE && a->e->weight < dist[a->aName-97])
dist[a->aName-97] = a->e->weight;
}
}
}
int main()
{
GraphType G;
init(&G);
//정점이 A~G
makeVertex(&G, 'a'); makeVertex(&G, 'b');
makeVertex(&G, 'c'); makeVertex(&G, 'd');
makeVertex(&G, 'e'); makeVertex(&G, 'f');
makeVertex(&G, 'g'); //정점 생성 완료
insertEdge(&G, 'a', 'b', 29); insertEdge(&G, 'a', 'f', 10);//그래프와 정점의 이름. 왼쪽부터 알파벳 순, 간선 추가
insertEdge(&G, 'b', 'c', 16); insertEdge(&G, 'b', 'g', 15);
insertEdge(&G, 'c', 'd', 12);
insertEdge(&G, 'd', 'e', 22); insertEdge(&G, 'd', 'g', 18);
insertEdge(&G, 'e', 'f', 27); insertEdge(&G, 'e', 'g', 25);
print(&G);
prim(&G, 'c');
return 0;
}💡 알고리즘 분석
prim의 알고리즘은 주 반복문이 정점의 수 n만큼 반복하고, 내부 반복문이 n번 반복하므로 O(n^2)의 복잡도를 가진다. kruskal의 알고리즘은 O(elog2e)이므로 희소그래프를 대상으로 할 경우에는 kruskal의 알고리즘이 적합하고, 밀집 그래프의 경우에는 prim의 알고리즘이 유리하다.
- 최단 경로
네트워크에서 정점 i와 정점 j를 연결하는 경로 중에서 간선들의 가중치 합이 최소가 되는 경로를 찾는 문제. 간선의 가중치는 비용, 거리, 시간등을 나타낸다.
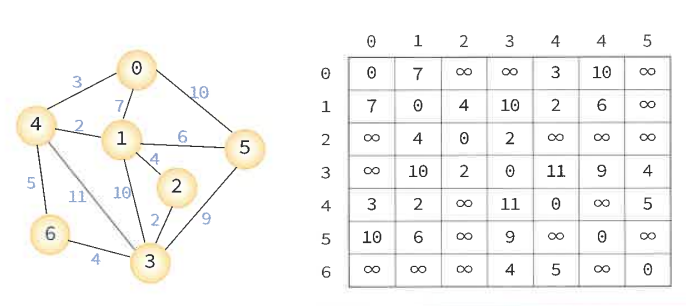
정점 0에서 정점 3으로 가는 최단 경로는 0, 4, 1, 2, 3 이고, 다른 경로도 존재하지만 이 경로가 가장 최단 거리이다.
- Dijkstra의 최단 경로 알고리즘
네트워크에서 하나의 시작 정점으로부터 모든 다른 정점까지의 최단 경로를 찾는 알고리즘. 최단 경로는 경로의 길이 순으로 구해진다.
distance[] = 시작정점에서 집합 S에 있는 정점만을 거쳐서 다른 정점으로 가는 최단 거리를 기록하는 배열
가중치는 가중치 인접 행렬에 저장되므로 가중치 인접 행렬이 weight이면 distance[w] weight[v][w]가 된다. 정점 v에서 정점 w로의 직접 간선이 없을 경우에는 무한대의 값을 저장한다.
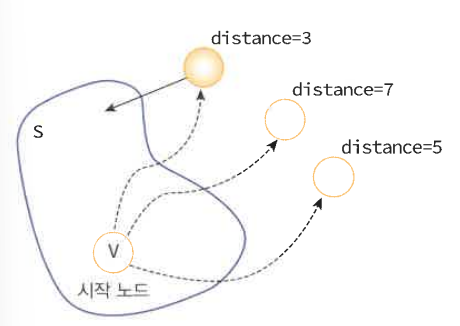
알고리즘의 각 단계에서 S안에 있지 않은 정점 중 가장 dist값이 작은 정점을 S에 추가한다.
새로운 정점 u가 S에 추가되면, S에 있지 않은 다른 정점들의 distance 값을 수정한다. 새로 추가된 정점 u를 거쳐서 정점까지 가는 거리와 기존의 거리를 비교하여 더 작은 거리로 dist 값을 수정한다.


void dijkstra(GraphType* G, element vName)
{
Vertex* v = findVertex(G, vName);
Vertex* p = NULL;
AdjacentVertex* a = NULL;
element minName;
dist[vName - 97] = 0; //시작 정점의 거리를 0으로 설정
for (int i = 0; i < G->vCount - 1; i++)
{
minName = getMinVertex(G); //방문하지 않은 정점 중에 distance가 제일 작은 점
v = findVertex(G, minName);
v->isVisit = TRUE; //방문 처리
printf("[%c](%d) ", v->vName, dist[v->vName - 97]); //점 방문을 출력으로 표시
printf("dist: ");
for (int i = 0; i < G->vCount; i++)
{
printf("[%d]", dist[i]);
}
printf("\n");
//방문한 점을 통해 인접 정점으로 이동할 것임임
for (a = v->aHead; a != NULL; a = a->next)
{
p = findVertex(G, a->aName); //인접 정점의 방문 여부를 검사하기 위해서
if (p->isVisit == FALSE && dist[v->vName - 97] + a->e->weight < dist[a->aName - 97])
dist[a->aName - 97] = dist[v->vName - 97] + a->e->weight;
}
}
}네트워크에 n개의 정점이 있다면, dijkstra의 최단경로 알고리즘은 주 반복문을 n번 반복하고 내부 반복문을 2n번 반복하므로 O(n^2)의 복잡도를 가진다.
