[자료구조] 트리(1) - 링크 표현법, 순회

8.1 트리

리스트, 스택, 큐 등은 선형 구조 이지만 트리는 계층적인 구조를 나타내는 비 선형구조다. 제약조건이 있는 그래프(사이클이 없는 연결 그래프

✨ 트리의 응용 분야: 계층적인 조직, 컴퓨터 디스크의 디렉토리 구조, 인공지능에서의 결정트리, 책의 목차 등

(1) 트리의 용어

노드: 트리의 구성요소, 데이터 저장 단위
루트: 부모가 없는 노드
서브트리: 하나의 노드와 그 노드들의 자손들로 이루어진 트리
단말노드: 자식이 없는 노드
비단말노드: 적어도 하나의 자식을 가지는 노드
레벨: 트리의 각 층의 번호
높이: 트리의 최대 레벨
차수: 노드가 가지고 있는 자식 노드의 개수(차수의 제한이 없으면 구현이 불가능하다)

✨순환적인 트리? 문제의 사이즈가 서브트리로 작아진다.

(2) 이진 트리

모든 노드가 2개의 서브 트리를 가지고 있으며, 서브트리는 공집합일 수 있다. 2개의 링크필드를 가지고 있으나 실존하는 자식 노드를 가지고 있냐 없냐의 차이. 없으면 단말노드이다. 서브 트리간의 순서가 존재한다. 왼 > 오

• 이진트리는 공집합일 수 있다.
• 루트와 왼쪽 서브트리, 오른쪽 서브트리로 구성된 노드들의 유한집합으로 정의된다. 이진 트리의 서브트리들은 모두 이진트리다.
• 노드의 개수가 n개 이면 간선의 개수는 n-1개
• 높이가 h인 경우, 최소 h개의 노드를 가지며 최대 2^h-1개의 노드를 가진다.
• n개의 노드를 가지는 이진트리의 높이는 최대 n이거나 최소 log2(n+1)의 상한이다.

(3) 이진트리의 분류

-포화 이진 트리: 트리의 각 레벨에 노드가 꽉 차있는 이진트리, 2^k-1개의 노드
-완전 이진 트리: 높이가 k일때 레벨 1부터 k-1까지는 노드가 모두 채워져 있고, 마지막 레벨 k에서는 왼쪽부터 오른쪽으로 노드가 순서대로 채워져 있는 이진트리. 마지막 레벨에서는 노드가 꽉차잇지 않아도 되지만 중간에 빈 곳이 있어서는 안된다. 포화이진트리는 항상 완전 이진 트리이다.

(4) 이진 트리의 표현

<4.1> 배열을 이용하는 방법

모든 이진 트리를 포화 이진 트리라고 가정하고, 각 노드에 번호를 붙여서 그 번호를 배열의 인덱스로 삼아 노드의 데이터를 배열에 저장하는 방법

• 완전 이진트리는 배열이 효율적이다.
• 곱하기 계산이 있어야 편하기 때문에, 인덱스 0은 사용하지 않는다.
• 기억공간의 낭비가 심하다.

✨ 노드 i의 부모 노드 인덱스 = i/2
✨ 노드 i의 왼쪽 자식 노드 인덱스 = 2i
✨ 노드 i의 오른쪽 자식 노드 인덱스 = 2i+1

<4.2> 링크 표현법

트리에서의 노드가 구조체로 표현되고, 각 노드가 포인터를 가지고 있어서 포인터를 이용해 노드와 노드를 연결하는 방법.

링크 표현법으로 구현된 트리는 루트 노드를 가리키는 포인터만 있으면 트리안의 모든 노드들을 접근할 수 있다. 연결리스트와 유사한 방법이다.

(5) 이진 트리 순회방법

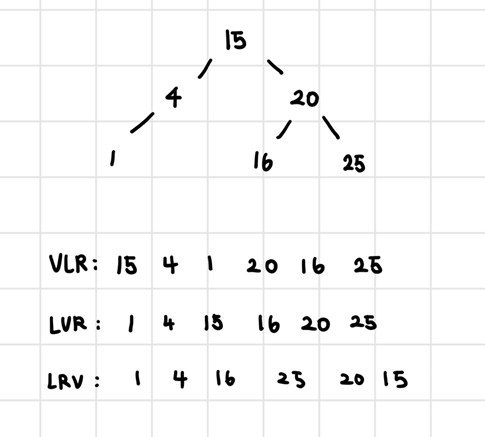
전위 순회(VLR): 자손 노드보다 루트 노드를 먼저 방문한다. 구조화된 문서출력에 응용
중위 순회(LVR): 왼쪽, 루트, 오른쪽 자손 순으로 방문한다. 수식트리에 응용
후위 순회(LRV): 루트노드보다 자손 노드를 먼저 방문한다. 디렉토리 용량 계산에 응용

// 링크 표현법 구현 방식

#include <stdio.h>
#include <stdlib.h>

typedef int element;
typedef struct TreeNode
{
    element data;
    struct TreeNode* left, * right; //왼쪽 자식노드, 오른쪽 자식 노드
}TreeNode;

이 전의 구현에서는, 노드를 표현할때 type을 만들었었다. 각각의 처리 함수에서 TreeNode의 주소를 리턴하지 않고, 이중 포인터를 리턴하지 않으려고 사용했었다. 그런데 트리에서는 모든 연산이 재귀적이기 때문에 노드를 타입으로 감싸면 매번 재귀호출이 이루어질 때마다 노드가 아닌 루트가 들어가게 된다. ✨반복문은 type이 편하고 순환문은 안하는게 편하다.

TreeNode* makeNode(element data, TreeNode* left, TreeNode* right) //노드를 생성하는 함수, 만든 노드의 주소를 리턴
{
    TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));
    node->data = data;
    node->left = left;
    node->right = right;

    return node;
}

void preOrder(TreeNode* root) //VLR
{
    if (root != NULL)
    {
        printf("[%d] ", root->data); //V
        preOrder(root->left); //L
        preOrder(root->right); //R
    }
}

void inOrder(TreeNode* root) //LVR
{
    if (root != NULL)
    {
        inOrder(root->left); //L
        printf("[%d] ", root->data); //V
        inOrder(root->right); //R
    }
}

void postOrder(TreeNode* root) //LVR
{
    if (root != NULL)
    {
        postOrder(root->left); //L
        postOrder(root->right); //R
        printf("[%d] ", root->data); //V
    }
}

int main()
{
    TreeNode* N4 = makeNode(1, NULL, NULL);
    TreeNode* N6 = makeNode(16, NULL, NULL);
    TreeNode* N7 = makeNode(25, NULL, NULL);
    TreeNode* N2 = makeNode(4, N4, NULL);
    TreeNode* N3 = makeNode(20, N6, N7);
    TreeNode* N1 = makeNode(15, N2, N3); //루트 노드
    //N1의 왼쪽자식은 N2, 오른쪽은 N3 아직 N2와 N3가 만들어 지기 전, 전방 참조 문제
    //N2, N3를 쓰려면 N1을 쓰기 전에 N2와 N3가 먼저 만들어져야 함

    // TreeNode *root = N1; 이라고 이름 붙여서 해도 됨. 근데 굳이임

    printf("pre : "); preOrder(N1); printf("\n");
    printf("In  : "); inOrder(N1); printf("\n");
    printf("post: "); postOrder(N1); printf("\n");
    return 0;
}

// 반복적인 순회 구현 코드, 스택 사용

#include <stdio.h>
#include <stdlib.h>
#define N 10

typedef int element;
typedef struct TreeNode
{
    element data;
    struct TreeNode* left, * right; //왼쪽 자식노드, 오른쪽 자식 노드
}TreeNode;

TreeNode* makeNode(element data, TreeNode* left, TreeNode* right) //노드를 생성하는 함수, 만든 노드의 주소를 리턴턴
{
    TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));
    node->data = data;
    node->left = left;
    node->right = right;

    return node;
}

typedef struct
{
    //스택에 들어가는건 노드
    TreeNode* data[N]; //트리노드를 집어넣는 스택 배열
    int top;
}StackType;

void init(StackType* S)
{
    S->top = -1;
}

int isEmpty(StackType* S)
{
    return S->top == -1;
}

int isFull(StackType* S)
{
    return S->top == N - 1;
}

void push(StackType* S, TreeNode* e)
{
    if (isFull(S))
    {
        printf("Overflow!\n");
        return;
    }
    S->top++;
    S->data[S->top] = e;
}

TreeNode* pop(StackType* S)
{
    if (isEmpty(S))
        return NULL;

    TreeNode* e = S->data[S->top];
    S->top--;
    return e;
}

//왼쪽 방문을 L, 오른쪽 방문을 R, 노드의 데이터 필드를 방문하는 것을 V
//L, R의 순서는 바뀔 수 없고, 할 수 있는건 V를 언제 방문하느냐.
//VLR, LVR, LRV 에 따라서 전 중 후위 순회

void preOrder(TreeNode* root) //VLR
{
    if (root != NULL)
    {
        printf("[%d] ", root->data); //V
        preOrder(root->left); //L
        preOrder(root->right); //R
    }
}

void iterInOrder(TreeNode* root)
{
    StackType S;
    init(&S);

    while (1)
    {
        for (; root != NULL; root = root->left)
            push(&S, root);

        root = pop(&S);

        if (root == NULL)
            break; //단말 노드를 찾았다.

        printf("[%d] ", root->data);
        root = root->right; //중위 순회, 왼쪽 순회하고 값도 출력했으니 오른쪽으로
    }
}
int main()
{
    TreeNode* N4 = makeNode(1, NULL, NULL);
    TreeNode* N6 = makeNode(16, NULL, NULL);
    TreeNode* N7 = makeNode(25, NULL, NULL);
    TreeNode* N2 = makeNode(4, N4, NULL);
    TreeNode* N3 = makeNode(20, N6, N7);
    TreeNode* N1 = makeNode(15, N2, N3); //루트 노드
    //N1의 왼쪽자식은 N2, 오른쪽은 N3 아직 N2와 N3가 만들어 지기 전, 전방 참조 문제
    //N2, N3를 쓰려면 N1을 쓰기 전에 N2와 N3가 먼저 만들어져야 함

    // TreeNode *root = N1; 이라고 이름 붙여서 해도 됨. 근데 굳이임
    //모든 정점을 방문하는 것이 가장 중요한, 기본적인 연산

    printf("Iter  : "); iterInOrder(N1); printf("\n");
    return 0;
}

이진트리의 왼쪽 노드들은 NULL노드에 도달할 때까지 스택에 추가되었다가 NULL노드에 도달하면 스택에서 하나씩 삭제된다. 이 삭제된 노드를 방문한 후에 노드의 오른쪽노드로 이동한다. 다시 이 노드의 왼쪽 노드들을 NULL 노드에 도달할 때까지 스택에 추가한다. 이 과정을 공백 스택이 될 때까지 되풀이 하면 이진 트리를 중위 순회할 수 있다.