[자료구조] 트리 (2) - 큐 레벨 오더

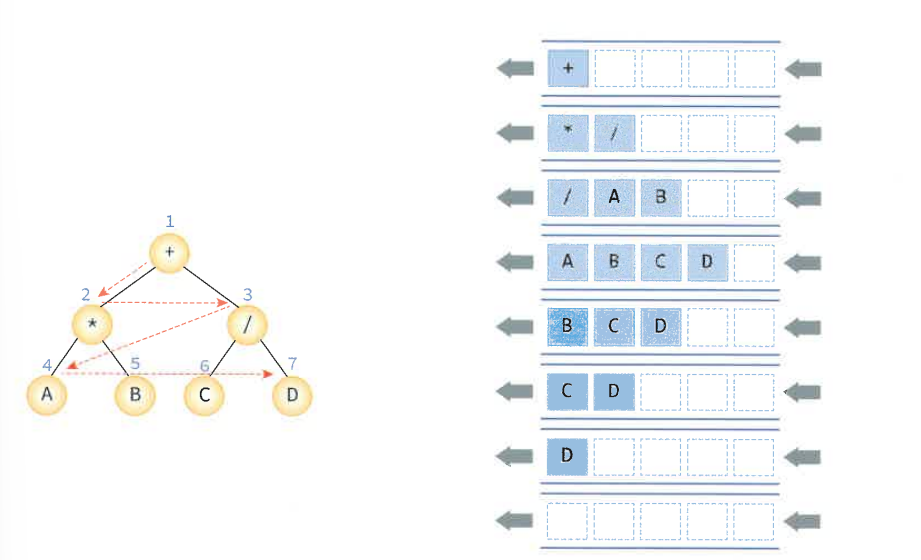
1. 레벨 순회

각 노드를 레벨 순으로 검사하는 순회 방법. 루트 노드의 레벨이 1이고 아래로 내려갈수록 레벨은 증가한다. 동일한 레벨의 경우에는 좌에서 우로 방문한다. 큐를 사용하는 순회 법이다. 큐에 있는 노드를 꺼내어 방문한 다음 그 노드의 자식 노드를 큐에 삽입하는 것으로 한번의 반복을 끝낸다. 이 반복은 큐에 더이상 노드가 없을 때까지 계속한다.

#include <stdio.h>
#include <stdlib.h>
#define N 10

typedef int element;
typedef struct TreeNode
{
    element data;
    struct TreeNode *left, *right;
}TreeNode;

TreeNode* makeNode(element data, TreeNode *left, TreeNode *right)
{
    TreeNode *node = (TreeNode*)malloc(sizeof(TreeNode));
    node->data = data;
    node->left = left;
    node->right = right;

    return node;
}

typedef struct
{
    TreeNode *data[N];
    int front , rear;
}QueueType;

void init(QueueType *Q)
{
    Q->front = Q->rear = -1;
}

int isEmpty(QueueType *Q)
{
    return Q->rear == Q->front;
}
int isFull(QueueType *Q)
{
    return Q->front == (Q->rear+1)%N;
}

void enqueue(QueueType *Q, TreeNode *e)
{
    if(isFull(Q))
        return;

    Q->rear = (Q->rear+1) % N;
    Q->data[Q->rear] = e;
}

TreeNode* dequeue(QueueType *Q)
{
    if(isEmpty(Q))
        return NULL;
    Q->front = (Q->front+1) % N;
    return Q->data[Q->front];
}

void levelOrder(TreeNode *root)
{
    QueueType Q;
    init(&Q);

    enqueue(&Q, root);

    while(!isEmpty(&Q))
    {
        root = dequeue(&Q);
        printf("[%d] ", root->data);

        if(root->left)
            enqueue(&Q, root->left);
        if(root->right)
            enqueue(&Q, root->right);
    }
}
void preOrder(TreeNode *root)
{
    if(root != NULL)
    {
        printf("[%d] ", root->data);
        preOrder(root->left);
        preOrder(root->right);
    }
}

자식 노드를 처리한 다음에 부모 노드를 처리해야 한다면 => 후위순회 부모 노드를 처리한 다음에 자식 노드를 처리해야 한다면 => 전위순회

현재 디렉토리 용량을 알려면 하위 디렉토리의 용량을 알아야지 계산할 수 있으니까

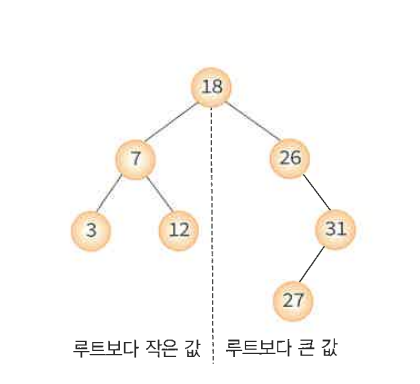
2. 이진 탐색 트리

이진 트리 기반의 탐색을 위한 자료 구조. 컴퓨터 프로그램에서 많이 사용되므로 탐색을 효율적으로 수행하는 것이 중요.

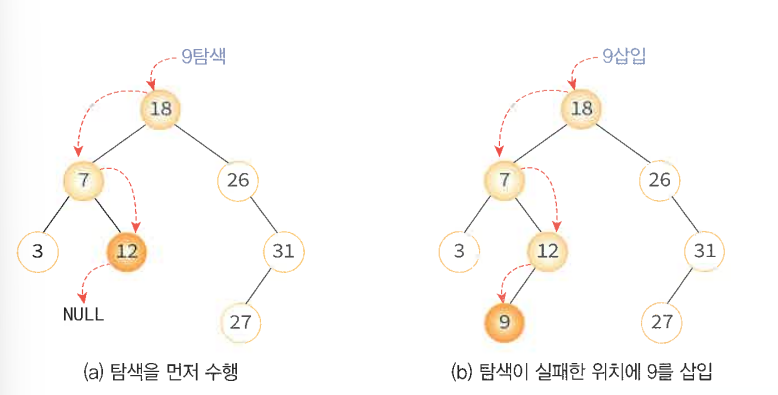
(1) 이진 탐색 트리 삽입 연산

삽입하기 전에 탐색을 수행한다. 같은 키 값을 갖는 노드가 없어야 하기 때문이고, 탐색에 실패한 위치가 바로 새로운 노드를 삽입하는 위치다. 키가 트리안에 없으면 유일한 키 값이기 때문에 탐색은 실패하고, 실패한 위치에 노드가 만들어 진다.

TreeNode* insertNode(TreeNode *root, element key)
{
	if(root == NULL)
    	return makeNode(key);
    
    if(key < root->key)
    	root->left = insertNode(root->left, key);
    
    else if(key > root ->key)
    	root->right = insertNode(root->right, key);
    
    return root;
}

(2) 노드 개수 구하기

탐색 트리 안의 노드 개수를 계산한다. 각 서브트리에 대해 순환 호출한 다음, 반환되는 값에 1을 더하여 반환한다.

int getNode(TreeNode* node)
{
    int count = 0;
    if(node !=NULL)
        count = 1 + getNode(node->left)+getNode(node->right); //노드를 방문할때 마다 1씩 증가.
    return count;
}

(3) 트리의 높이 구하기
서브트리의 반환 값 중에서 최대 값을 구하여 반환 + 1

int getHeight(TreeNode *node)
{
    int height = 0;
    if(node != NULL)
        height = 1 + max(getHeight(node->left), getHeight(node->right)); //일단 노드를 방문하는데, 방문한 노드가 단말 노드일떄만 1을 더한다.
        
    return height;
}

(4) 단말 노드 개수

트리안의 노드들을 전체적으로 순회하면서 왼쪽 자식과 오른쪽 자식이 동시에 0이 되면 단말노드이므로 1을 반환한다. 그렇지 않으면 비단말 노드이므로 각각의 서브트리에 대하여 순환 호출한 다음, 반환되는 값을 서로 더한다.

int getLeafCount(TreeNode *node)
{
    int count = 0;

    if(node != NULL)
    {
        if(node->left == NULL && node->right == NULL)
            return 1;
        else
            count = getLeafCount(node->left)+getLeafCount(node->right);
    }

    return count;
}

(5) 탐색

<5-1>순환적인 탐색 함수

TreeNode* search(TreeNode *node, element key)
{
	if(node == NULL) return NULL;
   if(key == node->key) return node;
   else if(key <node->key)
   	returnsearch(node->left , key);
   else
   	return search(node->right, key);
}

<5-1>반복적인 탐색 함수

 TreeNode* search(TreeNode *node, element key)
{
	while(node != NULL)
   {
   	if(key == node->key) return node;
       else if(key < node->key)
       	node = node->left;
       else
       	node = node->right;
   }
   return NULL; //탐색에 실패했을 경우 NULL 반환
}

(6) 이진 탐색 트리 삭제 연산

1. 삭제하려는 노드의 왼쪽 자식 노드가 없는 경우 (오른쪽 자식노드가 있을 수도, 단말 노드 일수도 있다)
✨ 이 노드의 부모 노드에 내 오른쪽 노드를 연결한다.
2. 오른쪽 자식 노드가 NULL이고, 왼쪽 자식 노드만 가지고 있을 때
✨ 부모노드에 내 왼쪽 서브트리의 루트를 연결한다. (어차피 항상 큰 값이다)
3. 왼쪽, 오른쪽 서브트리를 모두 가지고 있을 때
✨ 삭제하려는 값보다 큰 값중에 제일 작은 값을 데려와 덮어 씌우기 (연결 상태는 그대로) (또는 작은 값중에 제일 큰 값)

  #include <stdio.h>
#include <stdlib.h>
#include <time.h>

#define max(a,b) (((a)> (b)) ? (a) : (b))

typedef int element;
typedef struct TreeNode
{
  element key;
  struct TreeNode* left, *right; //왼쪽 자식노드, 오른쪽 자식 노드
}TreeNode;

TreeNode* makeNode(element key) //노드를 생성하는 함수, 만든 노드의 주소를 리턴턴
{
  TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));
  node -> key = key;
  node -> left = NULL;
  node -> right = NULL;
  
  return node;
}

void preOrder(TreeNode* root) //VLR
{
  if(root != NULL)
  {
      printf("[%d] ", root -> key); //V
      preOrder(root->left); //L
      preOrder(root->right); //R
  }
}

TreeNode* insertNode(TreeNode* root, element key)
{
  //루트를 움직여서 key를 찾고, NULL이면 넣는다.
  if(root == NULL)
     return makeNode(key); //노드를 만들었으면, 명령을 내린쪽에 만든 노드를 던져줘야함. 
     
  if(key < root->key)
      root->left = insertNode(root->left, key);
      
  else if(key > root->key)
      root->right = insertNode(root->right, key);
      
  return root;
  
}

int getNode(TreeNode* node)
{
  int count = 0;
  if(node !=NULL)
      count = 1 + getNode(node->left)+getNode(node->right); //노드를 방문할때 마다 1씩 증가.
  return count;
}

int getHeight(TreeNode *node)
{
  int height = 0;
  if(node != NULL)
      height = 1 + max(getHeight(node->left), getHeight(node->right)); //일단 노드를 방문하는데, 방문한 노드가 단말 노드일떄만 1을 더한다.
      
  return height;
}

TreeNode* minValueNode(TreeNode* root)
{
  TreeNode* p = root;
  while(p ->left != NULL)
  {
      p=p->left;
  }
  return p;
}

TreeNode* deleteNode(TreeNode* root, element key) //삭제할 키 값
{
  if(root == NULL) //삭제할 노드가 없다.
      return NULL;
  
  if(key < root->key)
      root->left = deleteNode(root->left, key); //재귀 호출
  else if(key > root->key)
      root->right = deleteNode(root->right, key);
  else 
  {
      //찾았을 경우, 실제 노드 삭제가 일어나는 곳
      //3가지 경우에 따라 삭제하는 방식이 다르다.
      if(root->left == NULL)
          {
              TreeNode* temp = root->right;
              free(root); //key 값이 없어짐
              return temp;
          }
      else if(root->right == NULL)
          {
              TreeNode* temp = root->left;
              free(root);
              return temp;
          }
      else
          {
              TreeNode* temp = minValueNode(root->right);//덮어 쓸 노드
              root->key = temp->key ; //값을 덮어 쓴다.
              root->right = deleteNode(root->right, temp->key); //덮어 쓰고, 오른쪽 서브 트리에 남아있는 값을 삭제한다.
          }
  }
  return root;
}

int main()
{
  TreeNode *root = NULL; //이진트리의 정의에서, 공집합도 이진트리임.
  //처음 트리가 만들어졌을때는 아무런 노드도 없는 상태
  srand(time(NULL));
  
  // for(int i=0;i<15;i++)
  //     root = insertNode(root, rand() % 50);
  //루트 노드를 삭제하는 경우도 있으니까, insert, delete 노드는 어떤 노드가 루트인지 주소를 리턴해줘야함.
  
  root = insertNode(root, 35); //현 시점에서의 트리를 주고, 35가 없으면 삽입
  root = insertNode(root, 68);
  root = insertNode(root, 99);
  root = insertNode(root, 18);
  root = insertNode(root, 7); root = insertNode(root, 3);
  root = insertNode(root, 12); root = insertNode(root, 26);
  root = insertNode(root, 22); root = insertNode(root, 30);
  
  
  
  preOrder(root); printf("\n");
  root = deleteNode(root, 30); preOrder(root); printf("\n");
  root = deleteNode(root, 26); preOrder(root); printf("\n");
  root = deleteNode(root, 18); preOrder(root); printf("\n");
  
  return 0;
}

(7) 이진 탐색 트리의 성능 분석

✨이진 탐색 트리의 탐색, 삽입, 삭제 연산의 시간 복잡도는 트리의 높이 h에 비례한다. O(h)
✨n개의 노드를 가지는 이진 탐색 트리의 평균적인 경우의 시간 복잡도는 O(log2h)이다. h = log2n의 상한 (최선의 경우)

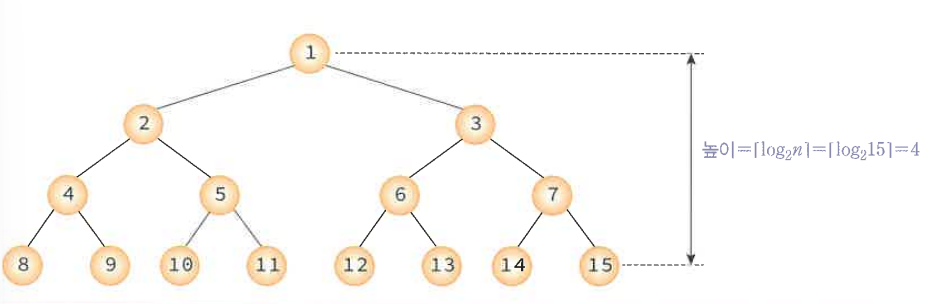
✨최악의 경우, h=n이 될때 O(n)

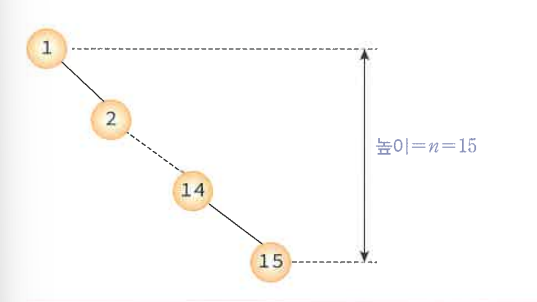
💡최악의 경우, 선형 탐색에 비하여 시간적 이득이 없다. 이를 방지하기 위해 트리를 균형지게 만드는 기법으로 AVL트리를 비롯한 여러 기법들이 개발되었다.