- 시간복잡도 (time complexity) : 얼마나 빠르게 결과를 출력하는가 ? : T(n)
int[] multiply ( int inputs, int multiplier){
int[] nums = new int[inputs.length];
for (int i = 0; i < inputs.length; i++) {
nums[i] = inputs[i] * multiplier;
}
retrun nums;
}이 함수를 실행했을때 실행 시간이 어느 정도일지 표현해 보고싶다.
int[] multiply ( int inputs, int multiplier){
int[] nums = new int[inputs.length];
for (int i = 0; i < inputs.length; i++) {
nums[i] = inputs[i] * multiplier;
}
retrun nums;
}실행시간 (running time) 이란 함수/알고리즘에 수행에 필요한 step수 라고 할수있다.
각 라인을 수행하기 위해 필요한 스텝 수는 상수라고 가정해보자
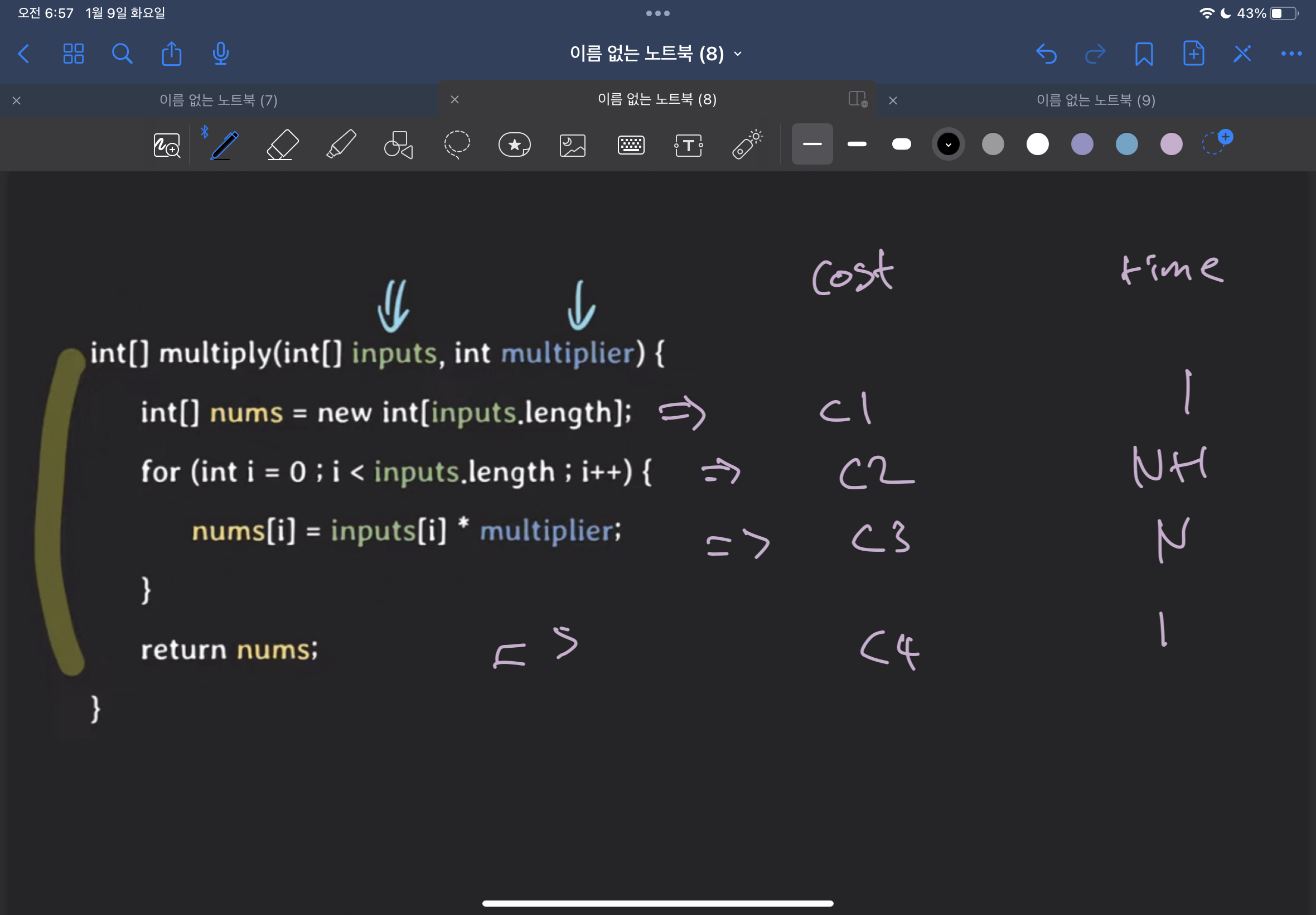
그림을 그려보면 이렇게 된다
각 라인별로 몇개의 스텝이 필요한지 상수로 표현해주었다.
옆에 time은 몇번 실행되는가 를 표현한것이다.
inputs 의 size 가 N이라 가정 했을때.
c1 은 한번
c2 는 N+1 이유 loop 를 탈출 할 때 검사를 한번 더 하기 때문이다
c3은 input size만큼 돌기 때문에 N번 돌 것이고
c4 는 한번만 실행된다.
이제 최종 적으로는 어떻게 계산해야 하는지 보겠다.
공식은 간단하다
cost 값과 time의 값을 곱하고 더하면 되는 것 이다
정확하게 수식으로 나타내 보겠다.
c1 x 1 + c2 x N+1 + c3 x N + c4 x 1 이렇게 나타낼 수 있다.
이제 수식을 정리해보겠다.
T(N) = c1 + c2 x (N+1)+ c3 x N+1
= (c2+c3) x N+1 + c1 + c2 + 1
= a x N + b
여기서 N은 input size 이다.
이렇게 최종적인 공식이 나올것이다.
여기서 갑자기 어? 왜 a가 나오지 할 수 있다 .
여기서 a는 (c2+c3) 이고 b는 (c1+c2) 이다.
이후 알아둬야 할 것 이 3가지 있다.
- 여기서 더 정확한 계산은 어렵다.
- N이 작을때엔 실행 시간이 의미가 없다.
N -> ∞ 일 때 실행 시간이 궁금하다.중요
여기서 제일 중요한 3번째를 알아보자.
우선 N -> ∞ 일때 일단 3가지를 꼭 머리속으로 생각하자
- N이 커질수록 덜 중요한 것은 제거.
- 최고차항만 의미가 있다.
- 최고차항의 계수는 의미가 없다.
이 3가지의 의미가 무엇인가?
위에 세운 공식을 다시 꺼내오자
T(N) = c1 + c2 x (N+1)+ c3 x N+1
= (c2+c3) x N+1 + c1 + c2 + 1
= a * N + b
이렇게 공식에 마지막
N이 커질수록 a * N + b 일때 최고차항 만 의미가 있기에.
a*N 만 의미가 있다는 것이다. b를 배제해 주도록 하자.
그리고 최고차항에서도 계수는 의미가 없기때문에 a를 배제해도 상관없다.
결국 N만 남는다 이때 우리는 θ(N) 세타N이라고 읽는다.
다시한번 정리해보자
N -> ∞ 으로 갈때 T(N) (input size) 가 계속 커질때 이 함수의 실행시간을 어떻게 표현할수있는가? θ(N) 이렇게 표현 할 수 있다는것을 알아보았다.
결국
- N이 커질수록 덜 중요한 것은 제거.
- 최고차항만 의미가 있다.
- 최고차항의 계수는 의미가 없다.
이 3가지 접근법 이런 분석방식을
점근적 분석(Asymptotic analysis) 이라고 한다.
임의의 함수가 N -> ∞ 일때 어떤 함수 형태에 근접해지는지 분석할수있다.
이때 표현방법은 θ(N) 점근적 표기법이라고 할 수있다.
마지막으로 정리해보자
시간 복잡도란?
함수의 실행 시간을 표현하는 것
주로 점근적 분석을 통해
실행 시간을 단순하게 표현하며
이 떄 점근적 표기법으로 표현한다.
결국 점근적 분석을 통해 점근적 표기법으로 표현한다고 많이들 말한다고 한다.
