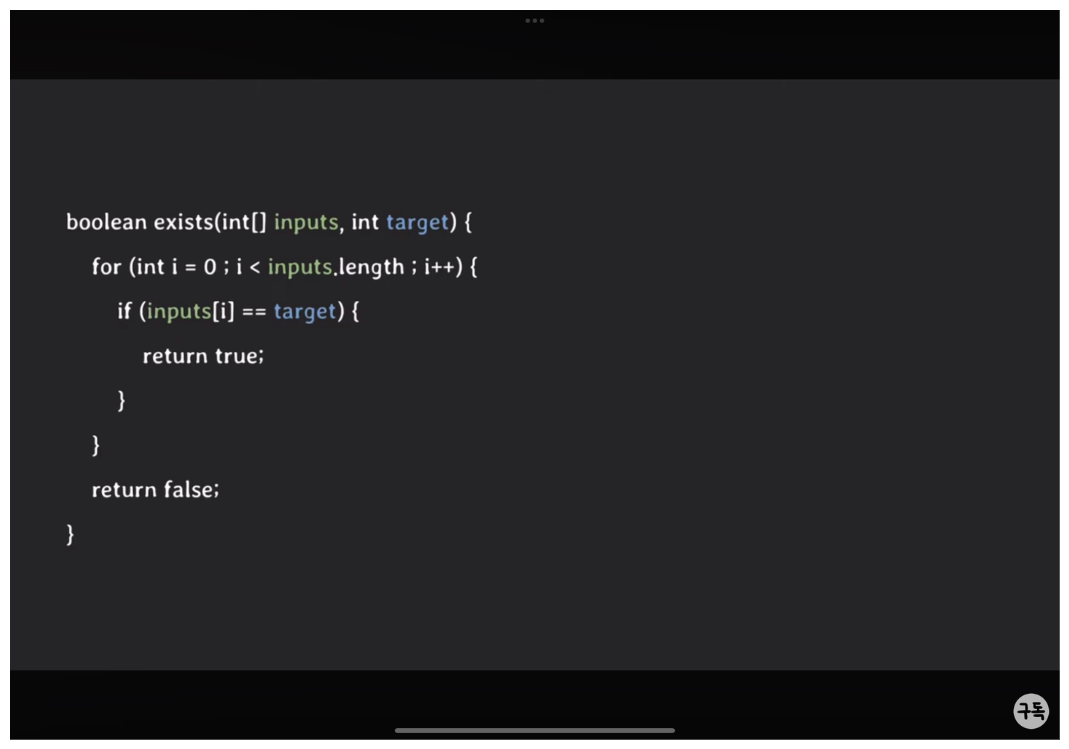
boolean exists(int[] inputs, int target){
for (int i = 0; i < inputs.length; i++) {
if(inputs[i] == target){
return true;
}
}
return false;
}새로운 코드를 봐보도록하자
이 함수는 inputs 에 target이 있는지 없는지 확인하는 코드이다.
이제 이 함수의 시간 복잡도를 구해보자.
주의
함수의 파라미터 데이터에 따라 실행 시간이 조금씩 다르다.
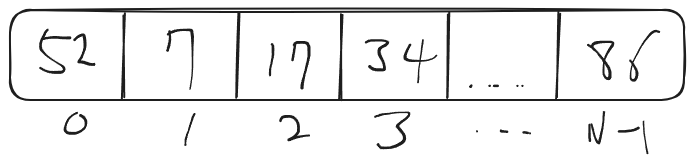
예를 들어서 이런 배열이 있다고 해보자
찾으려는 숫자가 52 즉 앞에 있다면 이 함수의 실행시간 은 빠를것이다.
하지만 찾으려는 숫자가 86 즉 마지막에 있다면 실행시간 은 느릴것이다.
이럴경우엔 case 를 분류해서 확인해보는 것 이 좋다.
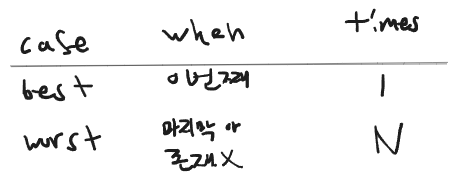
이렇게 표현해보았다.
best case는 찾으려는 값이 0번째 일 때
위에 배열에서 값이 52일 경우 함수는 딱 한번만 확인 할 것이다.
worst case 의 경우 찾으려는 값이 86 이거나 값이 없다면 이 배열의 size가 N이기 때문에
N번을 돌아야 한다.
이 함수 실행시간 을 문장으로 표현을 해보자면
lower bound (하한선)
함수 실행 시간은 아무리 빨라도 상수 시간 이상입니다.upper bound(상한선)
함수 실행 시간은 아무리 빨라도 상수 시간 이상입니다.하한선 부터 보자면 첫번째에 있든 두번째에있든 아무리 빨라도 상수 시간 그 자체를 말하는것이고
즉 아무리 빨라도 ~정도는 걸린다 라고 이해할 수 있으며.
상한선은 함수 실행 시간이 아무리 오래 걸려도 input size 값 에 비례하는 정도 거나 이하이고 아무리 오래걸려도 ~ 정도는 넘어서지않는다 라고 이해 할 수 있다.
이 하한선과 상한선을 점근적 표현으로 보자면
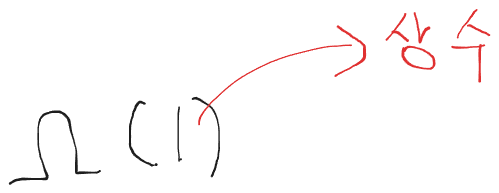
하한선은 이렇게 점근적 표현으로 나타낼수 있으며 빅 오메가 1로 읽을수 있다.
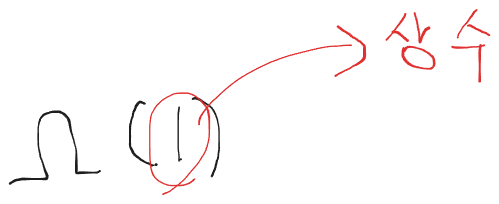
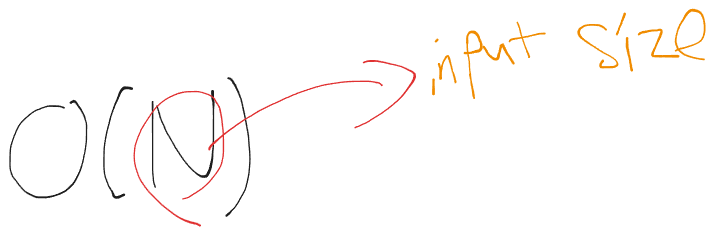
상한선은 이렇게 점근적 표현으로 나타낼수있다 빅오N으로 읽을 수 있다.
여기 하한선에
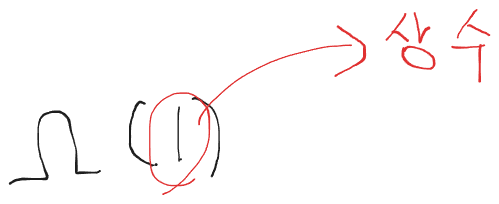
1이라고 되어있는부분은 상수 시간만큼 걸린다는것이다 즉 input size에 상관없이 상수 만큼 실행시간이 걸린다는것이고
상한선에 N이 의미하는것은 input size N에 비례하는 성질을 띈다라고 이해하면 된다.
결국
boolean exists(int[] inputs, int target){
for (int i = 0; i < inputs.length; i++) {
if(inputs[i] == target){
return true;
}
}
return false;
}이 코드를 표현하였을때
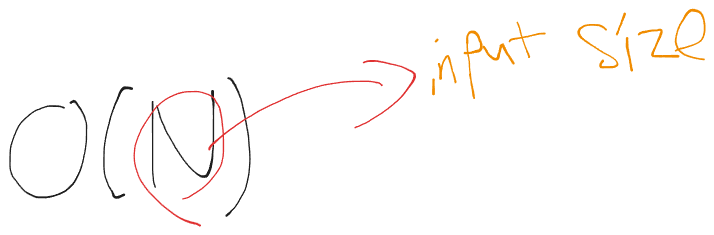
로 표현하거나

로 표현 할수도 있다.
둘다 맞는 표현이지만
우리는 worst case 를 의미깊게 보기때문에
보통은 빅오표기법 으로 많이 표현한다 .
