int findPositon(int[] sortedInputs , int target){
            ...
 }

정렬이 된 배열을 받는 값에서 내가 원하는 값(target)의 위치를 반환하는 그 검색을 binary search 라고 한다.

이때 binary search 하는 findPostion이라는 함수가 있다고 가정해보자.

이 경우 findPosition 에 대한 시간 복잡도는 어떻게 구할까?

worst case : 찾는게 없을 경우

로 가정해보자

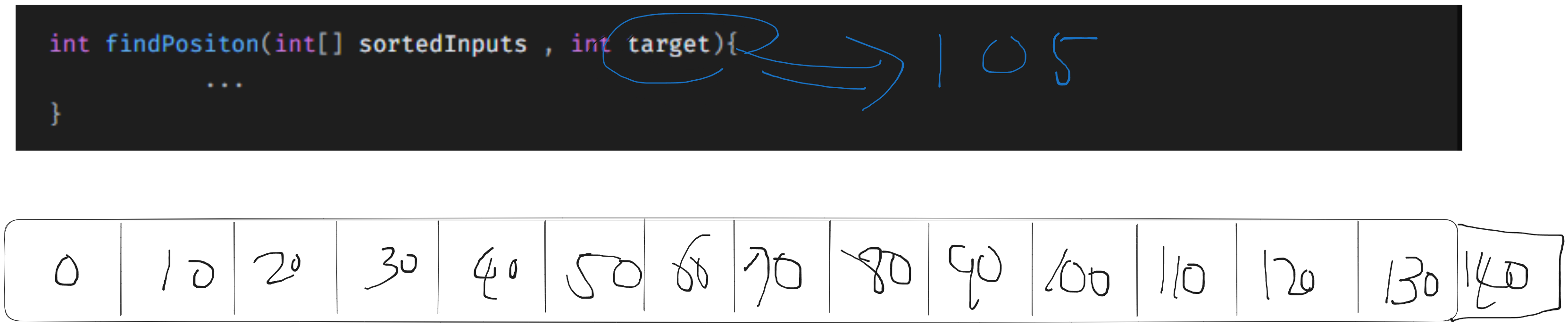
이때 배열을 탐색했을때

이렇게 하나씩 차근차근 확인 할 필요가 없다 이미 정렬된 배열이기 때문에 이렇게 확인하는 순간 성능이 떨어진다.

이럴 경우엔 가운데 부분부터 시작하면 된다.

이때 가운데에 있는 값과 내가 찾으려는 target(105)의 값을 비교를 해보자 이 경우에는

105가 더 크기때문에

70 보다 더 아래인 숫자에서는 찾을 필요가 없다 왜냐하면 이미 정렬이 된 배열이기 때문이다.

그 다음부분은 어떻게 해야하냐면

이런식으로 값을 제외시키면 된다

이때 제외시킨 값에서도 가운데 부분(110) 에서 확인을 해보면된다.

이때 110은 target(105)보다 큰 수 이기 때문에

80 90 100 / 110 / 120 130 140

가운데 110 을 기준으로 110이랑 110보다 큰수들을 제외 시키고 나머지 값들에서 확인해보면된다.

마지막으로 또 가운데 부분을 확인을 하면 된다.

가운데 숫자와 target 의 수를 비교해보자 이번엔 target이 가운데 수 보다 크다 이때는

왼쪽에 있는 수를 버리고 오른쪽에 있는 수랑 비교하면 된다.

최종적으로 100 과 target(105)를 비교해보자 이때 target의 값이 더 크기때문에 찾으려는 값이 나오지 않는걸 알수있다.

이때

worst case에서 몇번의 횟수로 이 함수가 끝이 났냐? 이것이 궁금한것이다.

이것을 알아야 이 함수의 worst case에서 시간복잡도를 구할수있을 태니깐..

이 규칙을 보면 한번 씩 돌아갈때마다 배열이 절반씩 사라지는 패턴을 가지고 있는이 보인다.

즉

매번 실행할 때 마다 1/2 씩 사이즈가 줄어든다 몇 번 만에 사이즈는 1이 되는가?

이것이 중요한것이다.

이것을 수식으로 나타내게 된다면

input size 를 N이라고 했을 때

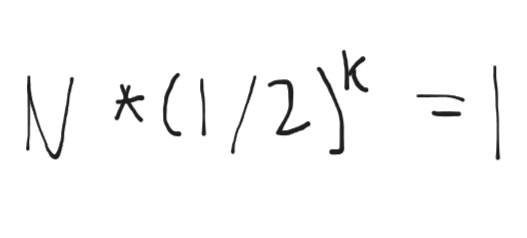
N을 k 번 1/2로 나누어 주 었더니 최종적으로 1 이 나오더라 이때 k를 구하는게 목적이다

수식을 적어보겠다.

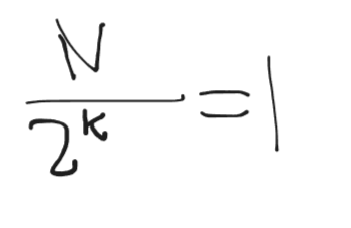
2.

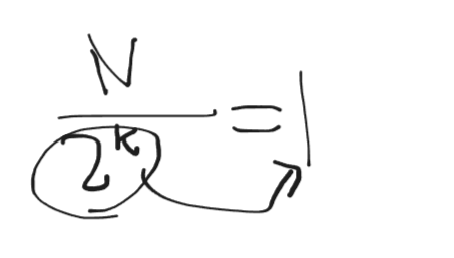
3.

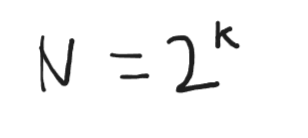
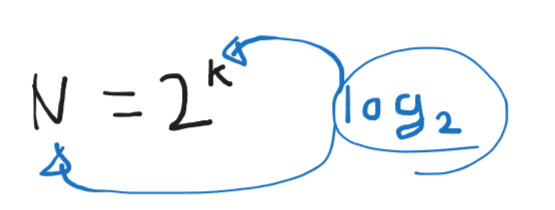
양쪽에 log2를 붙이게 되면

최종적으로

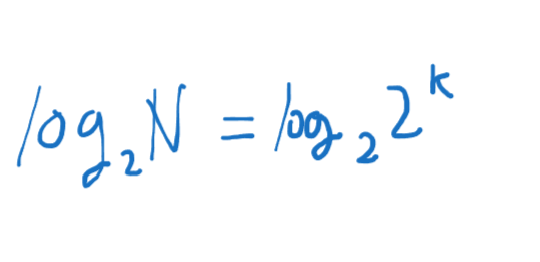
이렇게 된다 최종적으로 log2가 날라가기 때문에

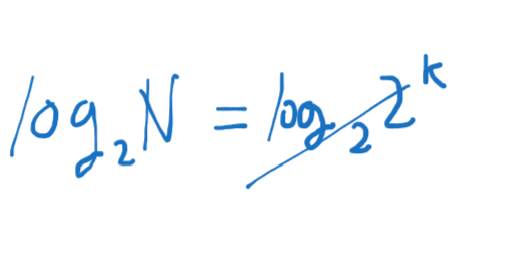
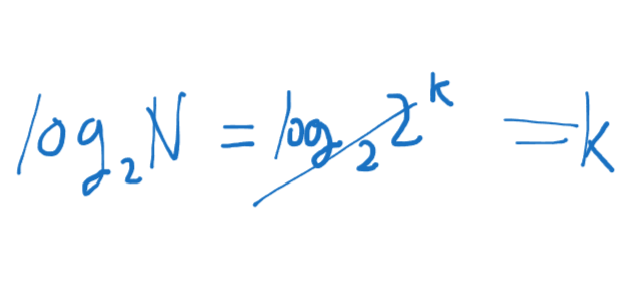
k가 남게 된다

최종수식은 worst case 일 경우 몇 번을 실행 하였는가를 구하고 싶은경우

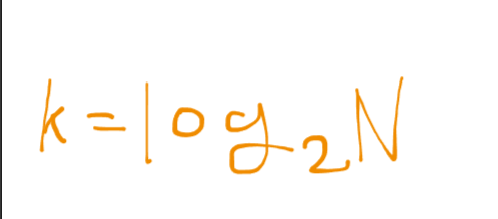
이렇게 나올것이다 이 것을 점근적 표현으로 나타나게 되면

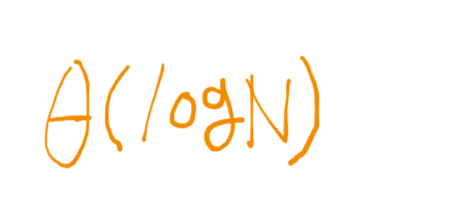
으로 나타낼수 있게 된다.

그렇다면 best case일 경우에는 ?

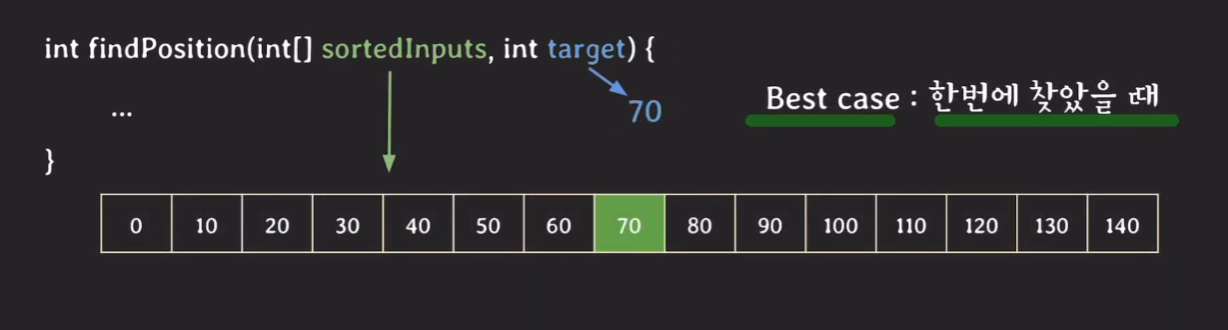
target의 값이 70일때 가운데 숫자가 70이므로 한번에 찾게된다

이 경우에 시간복잡도는

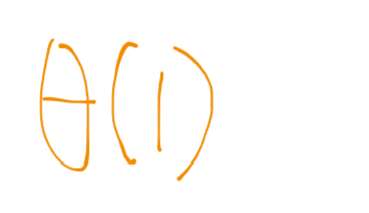
가 된다.

결국

 int findPositon(int[] sortedInputs , int target){
            ...
 }

이 함수의 시간복잡도는?

lower bound를 사용하여

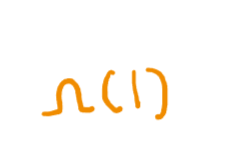
으로도 표현할수 있고.

upper bound 를 사용하여

이렇게 표현할수있다.

case별 시간 복잡도는 ?

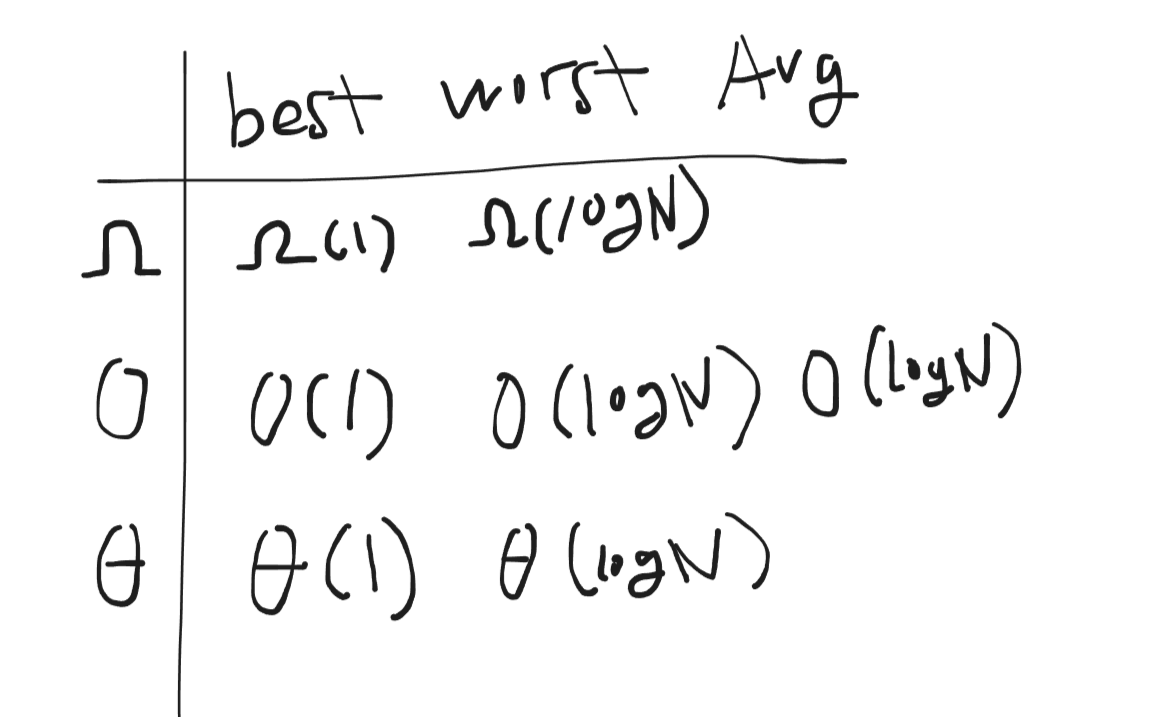
이렇게 나타낼수 있다.