시간 복잡도 를 알아보자 - 03 case별로 시간복잡도를 구해보자

저번 시간에 다루웠던 코드를 다시 가져와 시간 복잡도를 구해보자

boolean exists(int[] inputs, int target){  
    for (int i = 0; i < inputs.length; i++) {  
        if(inputs[i] == target){  
            return true;  
        }  
    }  
    return false;  
}

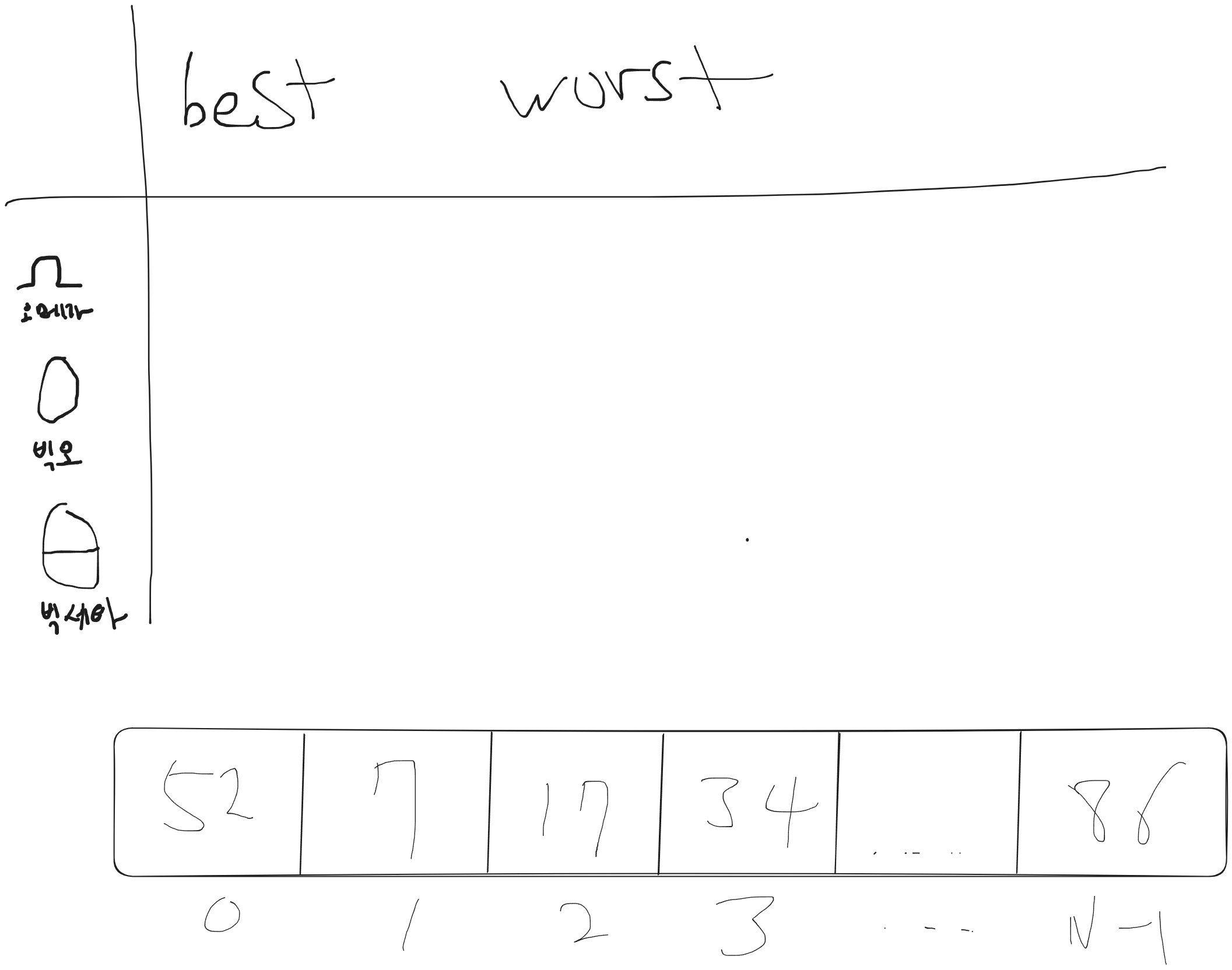
그림으로 배열을 만들고 case별로 나누어보았다.

오메가와 빅오 는 저번 게시글에서 다뤘다 이번에는 세타까지 알아보자.

일단 첫번째 best case에서 오메가와 빅오는 둘다 찾으려는값이 첫번째에 있을 경우다.

이 경우에는 upper bound 로 표현을하든 lower bound 로 표기을 하든 둘다 상수 시간에 끝날것이다.

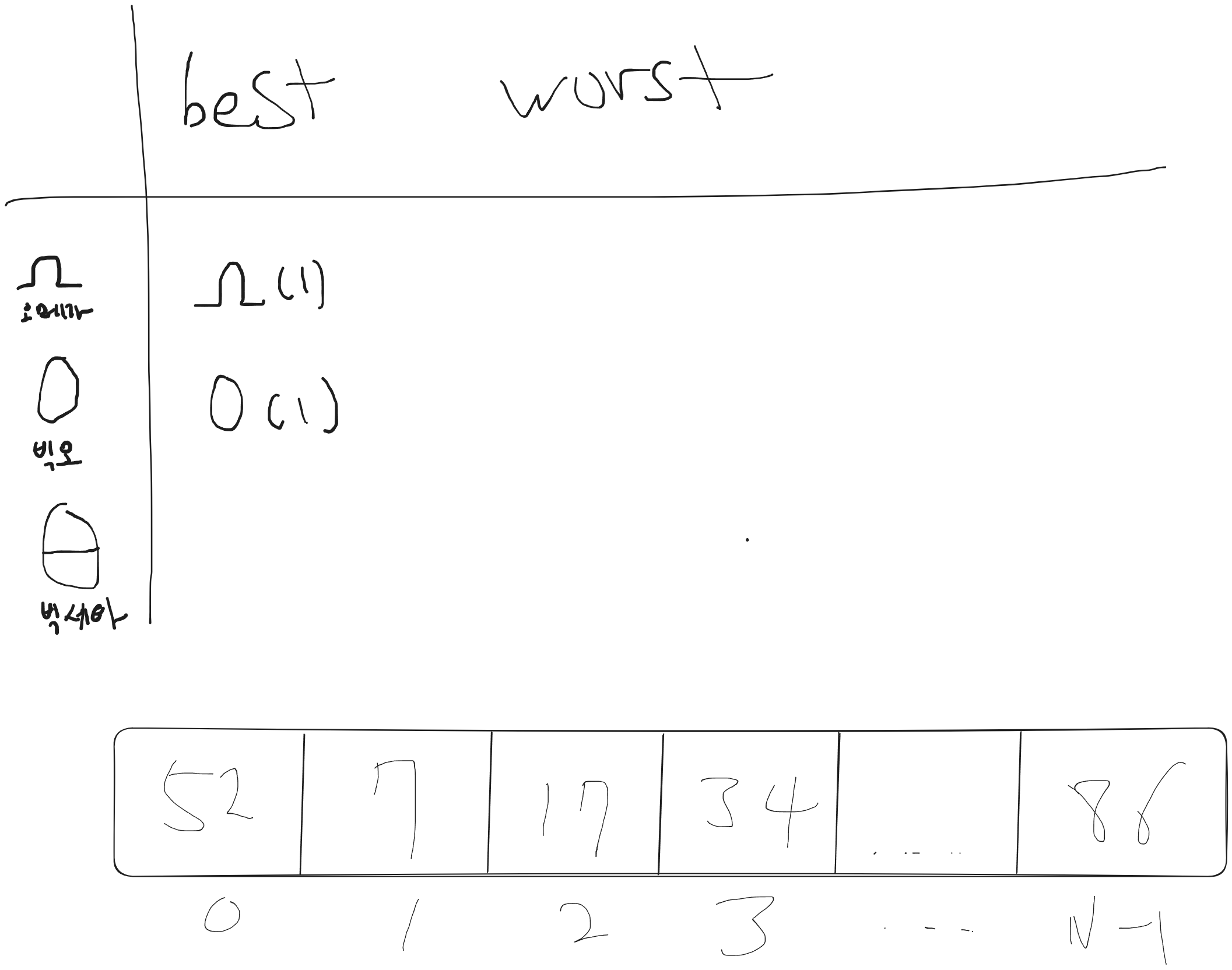
즉 이렇게 표기를 하면 lower bound 도 상수시간 upper bound 도 상수 시간이라는 것이다.

그러므로 둘다 똑같다 라는것이다 이 경우에는 세타로도 표현이 가능하다.

이 세타 표기법은 lower bound 와 upper bound가 즉 하한선과 상한선이 같을때 세타 표기로도 표현 할 수 있는것이다.

이 개념은 worst도 같다.

worst 의 조건은 찾으려는 값이 마지막에 있거나 또는 값이 존재하지 않거나 이다.

즉 lower bound 도 N만큼 찾아야하는것이고 upper bound 도 N만큼 찾아야하는것이다.

이 말은 즉 lower bound 와 upper bound가 같을때

이런 식으로 하한과 상한선이 같은 값을 돌아야할때 세타표기법 으로 상한선과 하한선이 아주 가깝게 같은 형태를 띈다 라고 하여 tight bound 라고 할수있다.

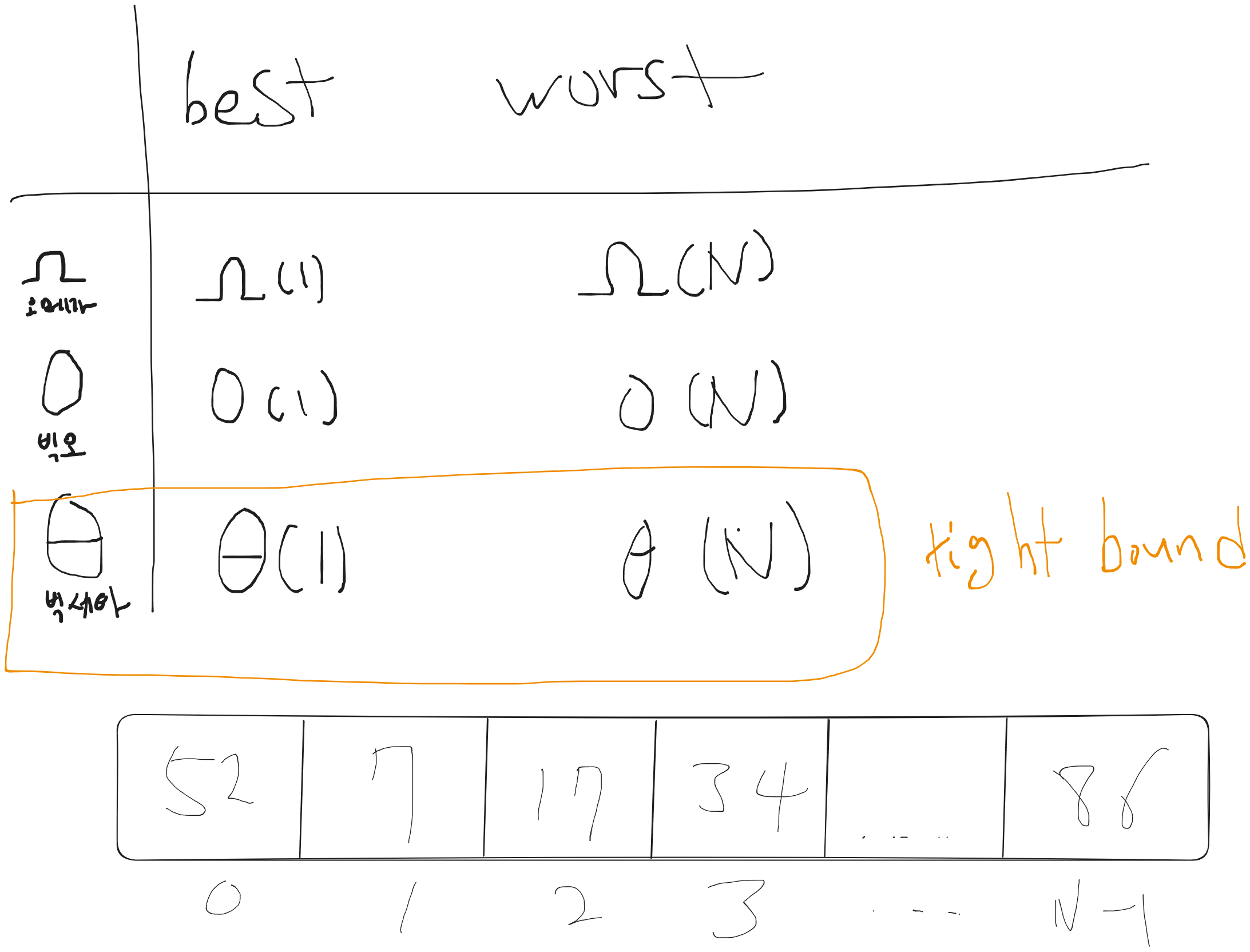
즉 우리는 이걸보고 해석을하자면

worst 일경우 세타(N)으로 표기하게 된다면 아 lower bound 와 upper bound 가 input size 즉 N을 비례하는 형태를 띄는구나 라고 해석 할 수 있다.

이것을 보고 상한선과 하한선을 알수있게 된다.

이제 마지막으로 Avg (에버리지) case에 대해서 알아보자

Avg(에버리지)란?

best case 와 worst case 를 제외한 즉 평균적으로 일반적으로 실행시간이 되는가 ?

라고 할수있다 하지만 조금 애매하다.

그림으로 설명해보겠다

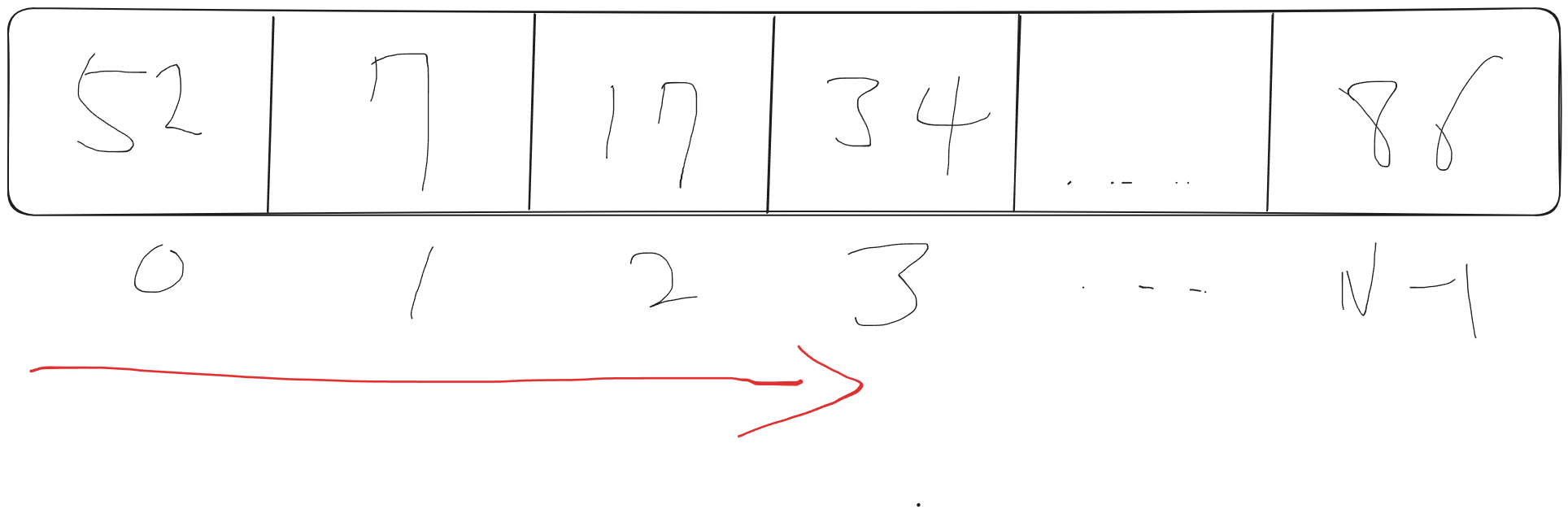
이 배열에서 찾아가다 절반정도 갔을때 내가 찾는 값이 있었다 라고 가정해보자

적어도 절반정도 찾아보았기 때문에.

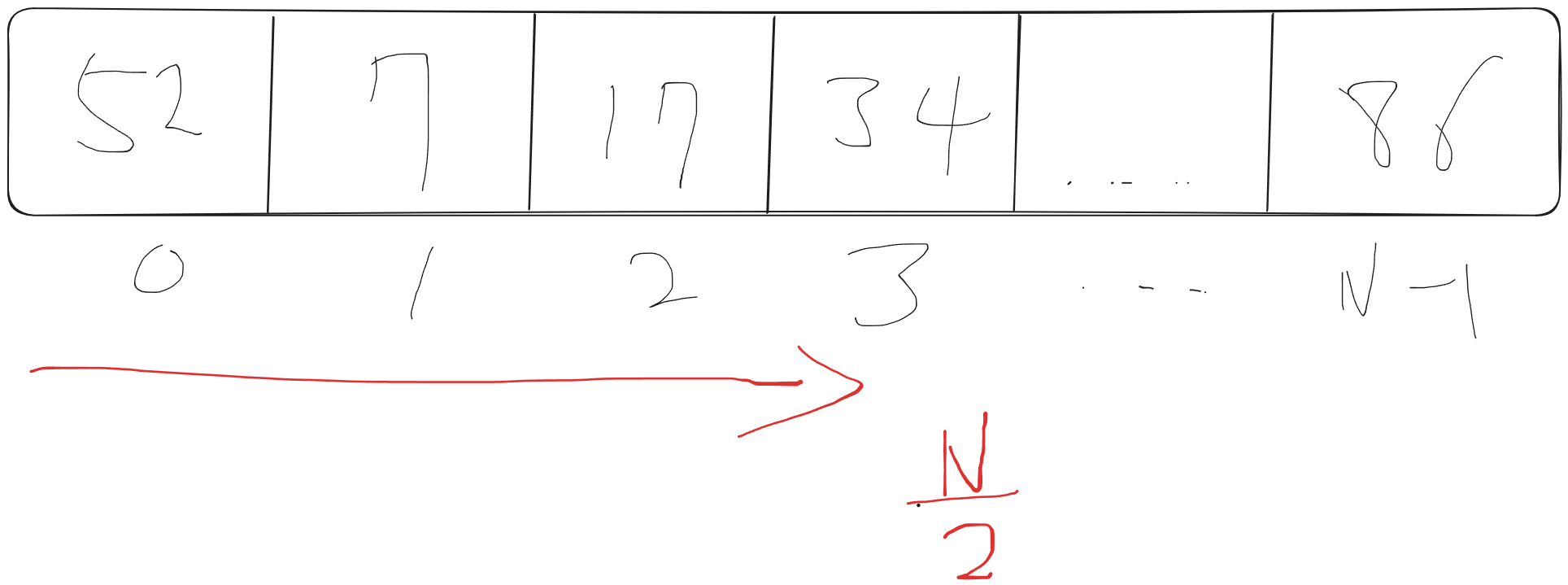
2/N 이라 표현할수 있다 하지만 최종적으로 점근적으로 접근하기 때문에 계수는 필요없다.

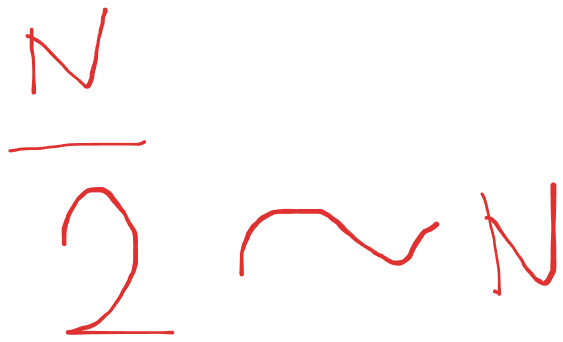
이런 성질을 나타낼 것이다.

이때 어떤 표현방법으로 나타낼것인가 하면.

바로 빅오(N)으로 표현 할수 있다.

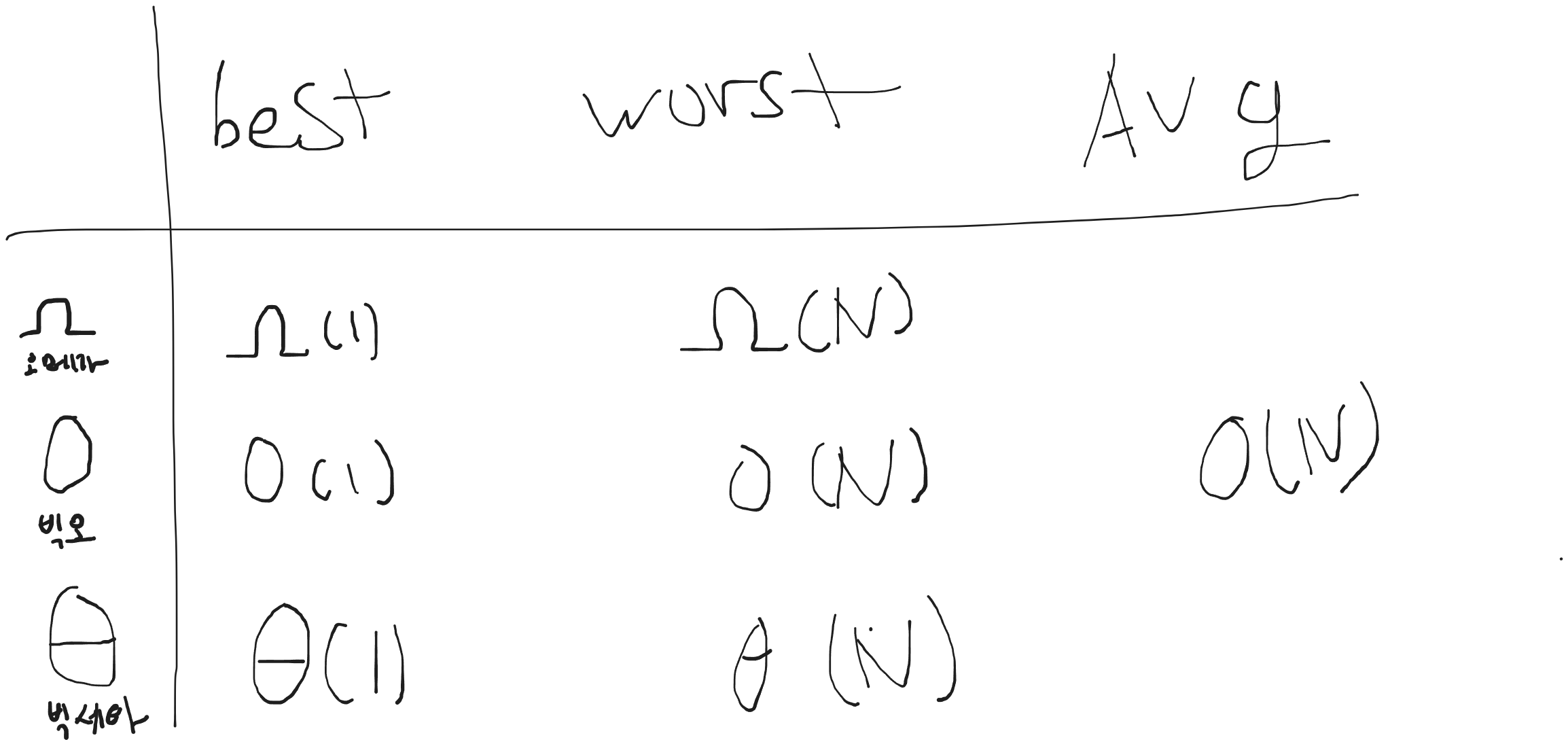
여기서 빅 오메가로 표현하거나 세타로 표현하기는 조금 애매하다

avg case 의 upper bound가 N으로 확실할거 같은데 lower bound 를 어떻게 봐야하냐가 애매해다.

이런 경우에는 빅오(N) 만 사용하여 upper bound만 표현하는것이다.

마지막으로 정리 해보자

점근적 표기법

Ω	O	Θ
lower bound	upper bound	tight bound

case 분류

best	worst	average
최단 시간 실행	최장 시간 실행	일반적인 실행