Lec 01. Introduction; Machine Learning for Graphs

<Course Outline>
- Why Graphs
- Applications of Graph ML
- Choice of Graph Representation
1.1 - Why Graphs
: Graphs are a general language for describing and analyzing entities with relations/interactions.
Types of Networks and Graphs
- Networks ( = Natural Graphs, 자연적으로 그래프 구조로 생긴 것)
- Social networks
- Communications and transactions
- Biomedicine (genes/proteins)
- Brain connections
- Graphs (as a representation of relational structure, 관계를 표현하기 위해 그래프로 모델링 한 것)
- Information/knowledge
- Software
- Similarity networks: Connect similar data points
- Relational structures: Molecules, Scene graphs, 3D shapes, Particle-based physics simulations
💡 Main question : How do we take advantage of relational structure for better prediction?
복잡한 + 많은 관계를 relational graph로 모델링함으로써 더 좋은 성능을 기대할 수 있음!
⇒ But, 현대의 딥러닝 기법은 단순한 sequences & grid 구조의 데이터 타입을 위해 디자인 됨.
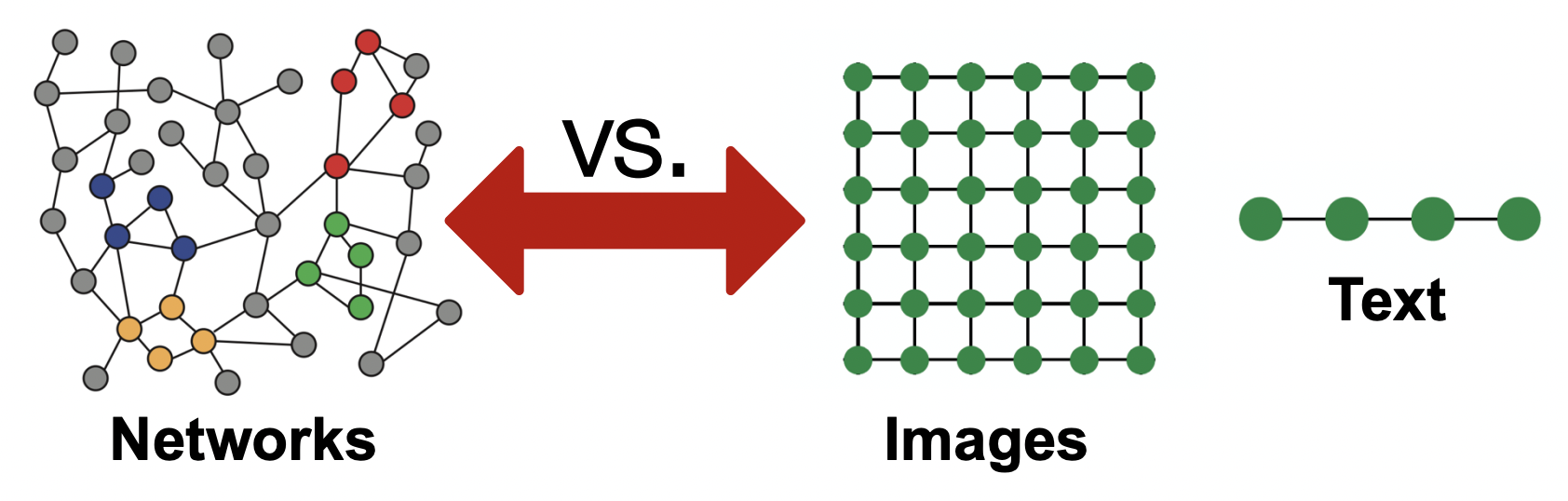
대표적으로 sequence & grid한 데이터 구조인 Images / Texts 에 비해 네트워크는 더 복잡한 구조를 가지고 있음
- 크기가 다양하고, 복잡한 모양을 가짐
- 위, 아래, 왼쪽, 오른쪽과 같은 공간상의 위치(spartial locality)가 없음
- 정해진 순서나 (출발점 같은) 기준점이 없음
- dynamic하며 multimodal features를 동시에 포함하기도 함
This Course ...
💡 question : 어떻게 하면 Graph와 같은 complex한 data에 딥러닝을 적용할 수 있을까?
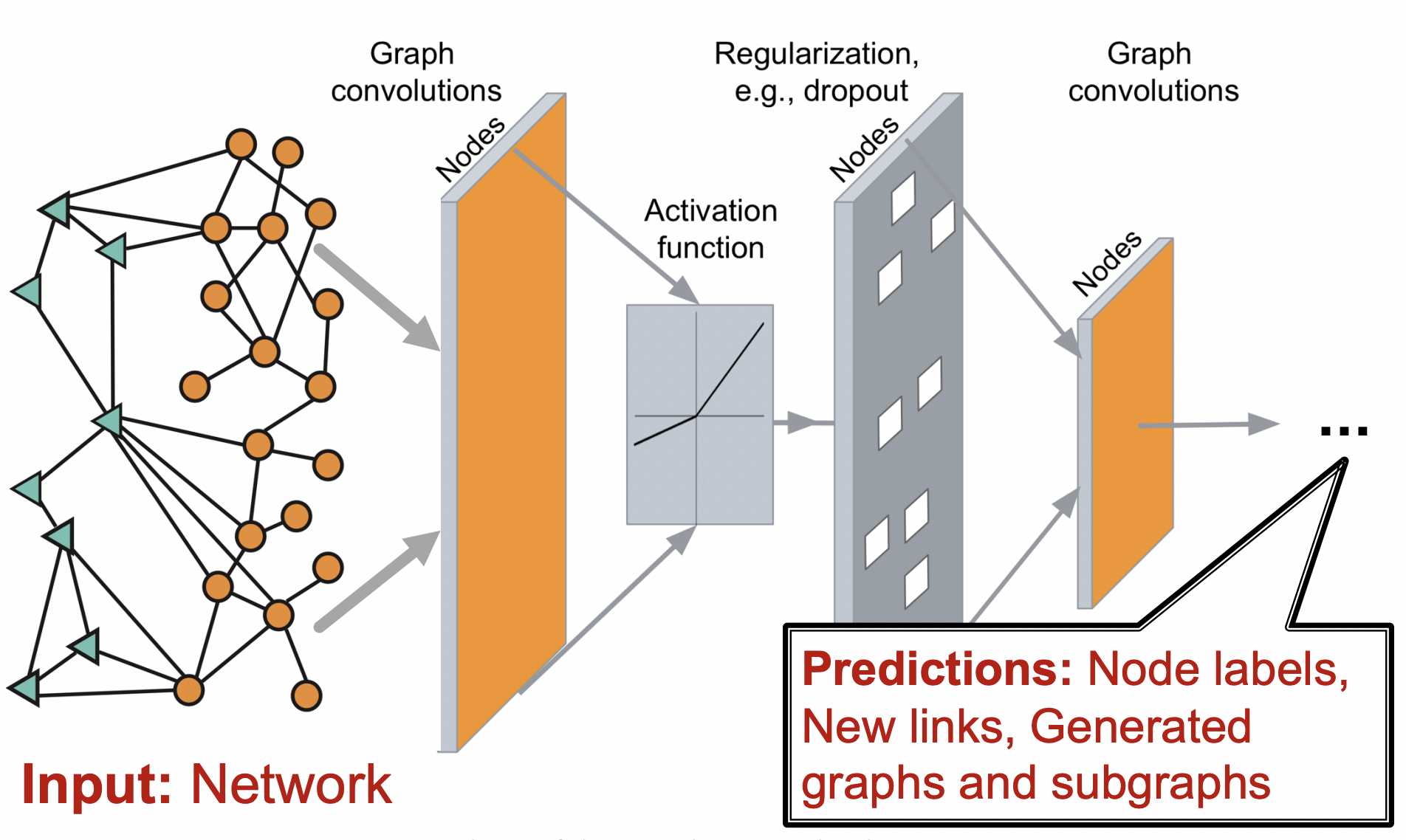
- input : Network
- output : Predictions
위 과정을 End-to-End로 할 수 있는 neural network architecture를 디자인
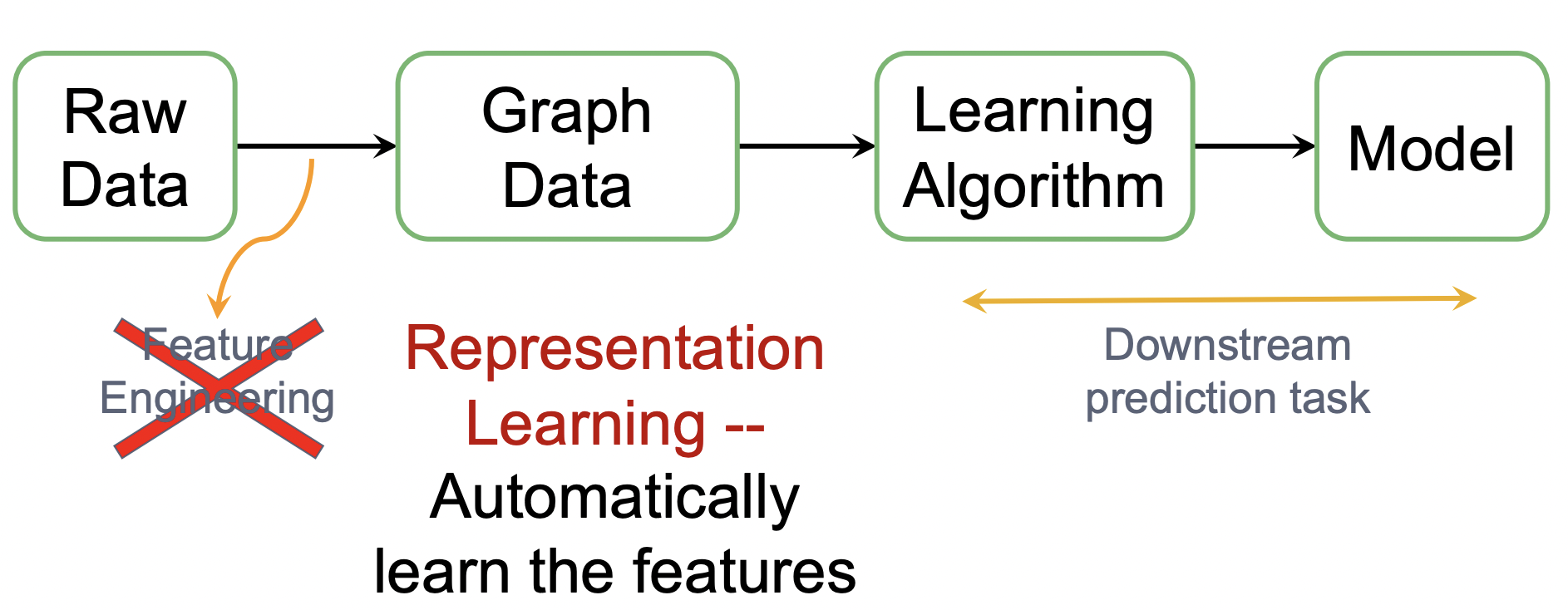
엔지니어가 적절한 feature를 디자인 하는데 많은 노력이 필요했던 전통적인 Feature Engineering (사용 X) → 그래프를 통해 downstream prediction task에 필요한 피처를 자동으로 학습하는 Representation Learing (O)
Representation Learning이란?
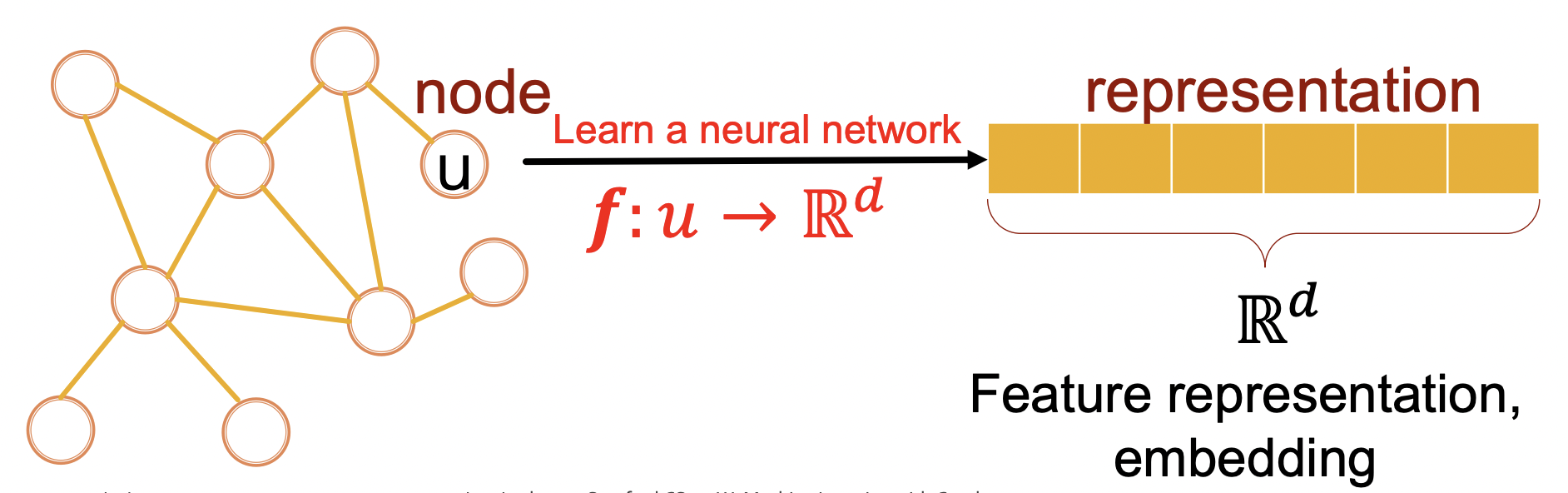
- 그래프의 node를
d-demensional vector로 임베딩 - 유사한 노드가 Embedding Space에 가까이 위치하도록 매핑
1.2 - Applications of Graph ML
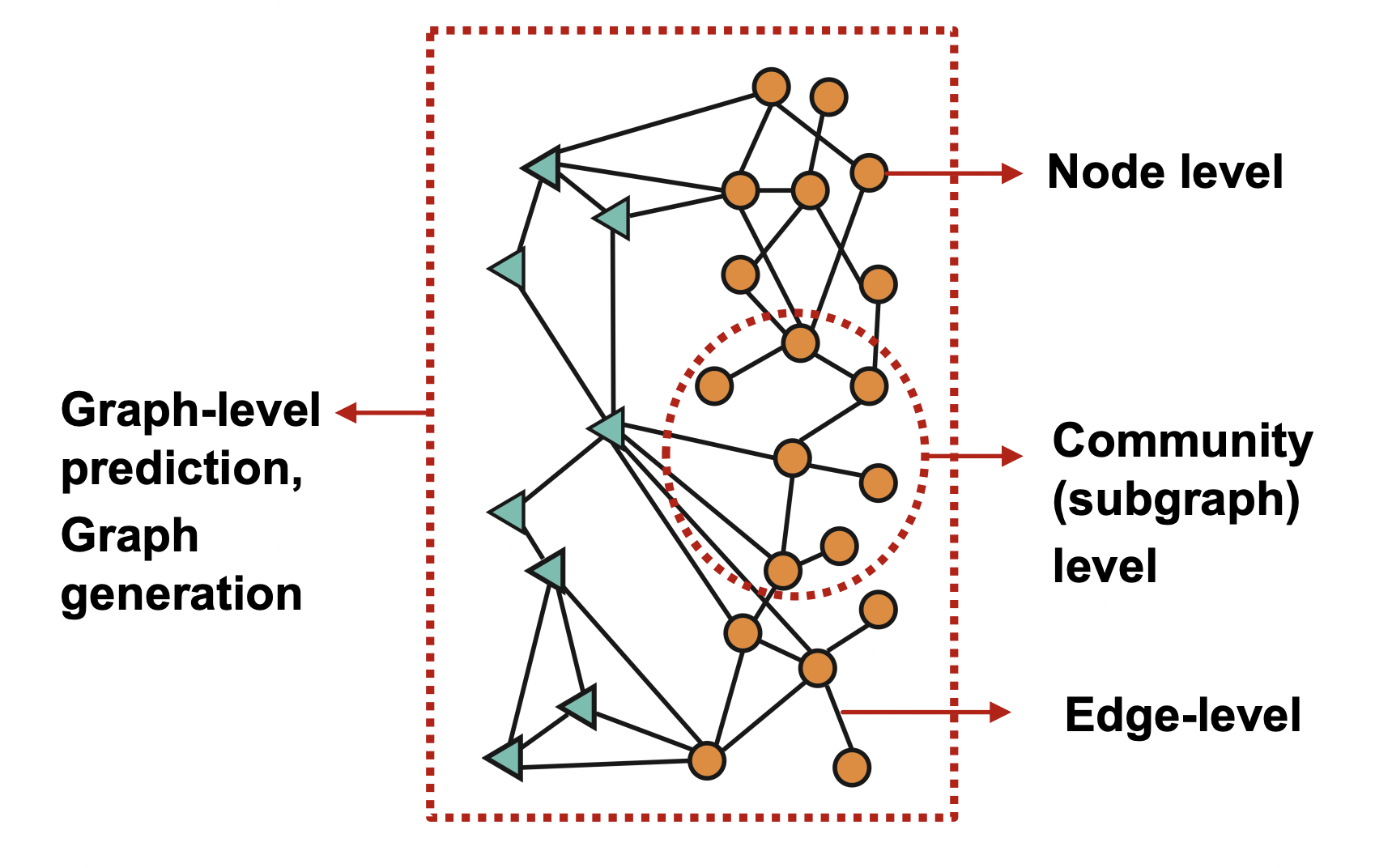
Classic Graph ML Tasks
- Node-level ML Tasks (Node classification): Predict a property of a node
- Example:
- Categorize online users / items
- Protein Folding (e.g. AlphaFold) : 공간 상에서 노드의 위치를 예측
- Example:
- Edge-level ML Tasks (Link prediction): Predict whether there are missing links between two nodes
- Example:
- Knowledge graph completion
- Recommender systems (e.g. PinSage): user-item interaction 예측
- Given a pair of drugs → predict adverse side effects
- Example:
- Subgraph-level ML Tasks:
- Traffic Prediction
- Clustering: Detect if nodes form a community
- Example: Social circle detection
- Graph-level ML Tasks:
- Graph generation: Drug discovery
- Example:
- Antibiotic Discovery
- Molecule Generation / Optimization
- Example:
- Graph evolution: Physical simulation
- Graph classification: Categorize different graphs
- Example: Molecule property prediction
- Graph generation: Drug discovery
: 데이터 및 가능한 경우의 수가 많을 때 verify할 가치가 있는 Testset을 빠르게 찾는 Simulator의 역할
1.3 - Choice of Graph Representation
Components of a Network
- Objects: nodes, vertices : denoted as
- Interactions: links, edges : denoted as
- System: network, graph : denoted as
How to build a graph:
- What are nodes?
- What are edges?
⇒ Choice of the proper network representation of a given domain/problem determines our ability to use networks successfully: The way you assign links will determine the nature of the question you can study
Directed vs. Undirected Graphs
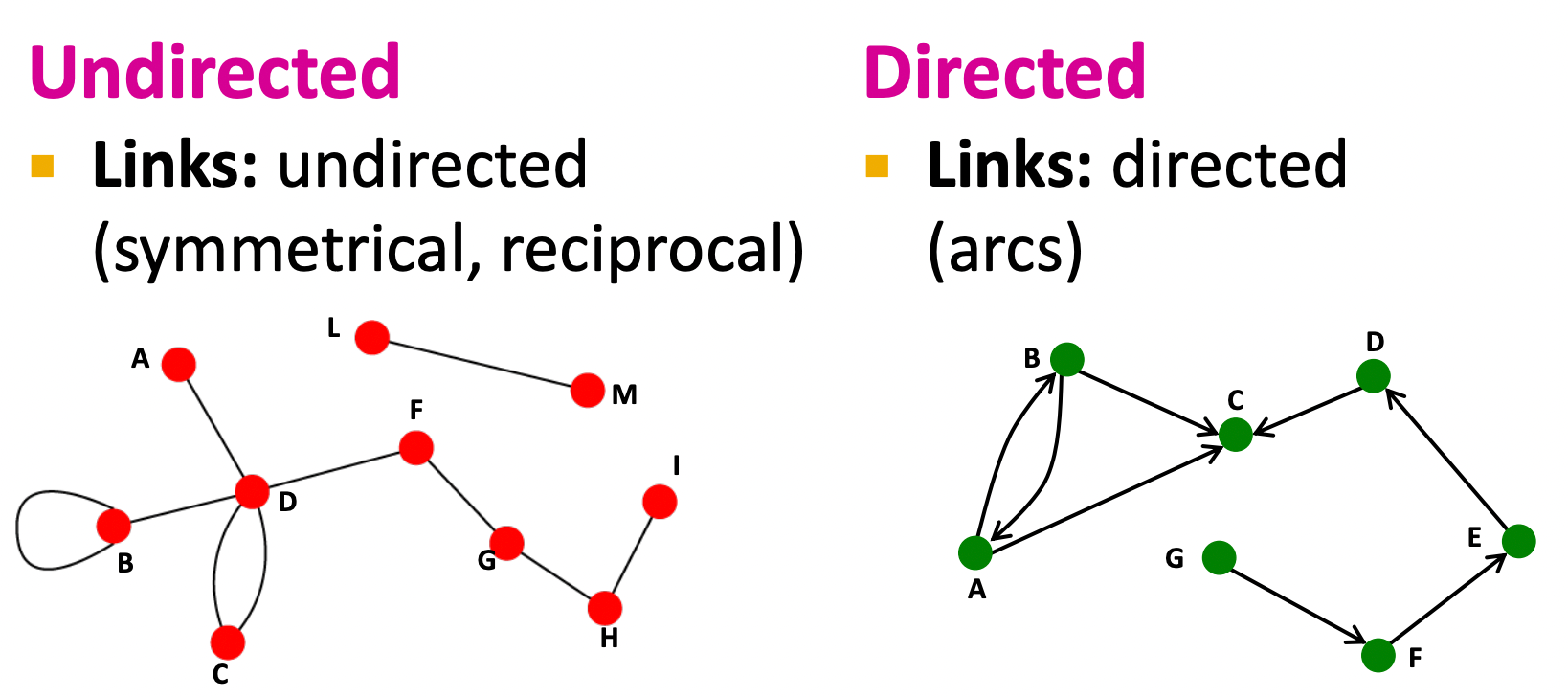
1) Directed
- Node degree, : node 와 인접한(연결된) 엣지의 개수
- Avg. degree :
2) Undirected
- source → destination 이 존재
- in-degree,
out-degree, - total degree, =
- Avg. degree =
- Source: Node with = 0
Sink: Node with = 0
Bipartite Graph (이분 그래프)
: 두가지 diffirent types의 노드 종류를 가지며, 오직 다른 종류의 노드와 상호작용(같은 종류의 노드끼리는 연결되지 않음)하는 그래프를 말함.
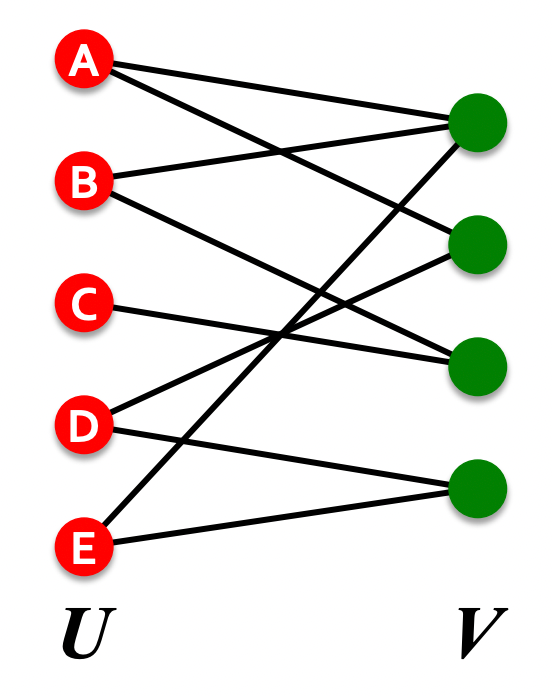
→ 이를 Folded Network 개념으로 나타낼 수 도 있음.
Folded(=Projected) Bipartite Graphs
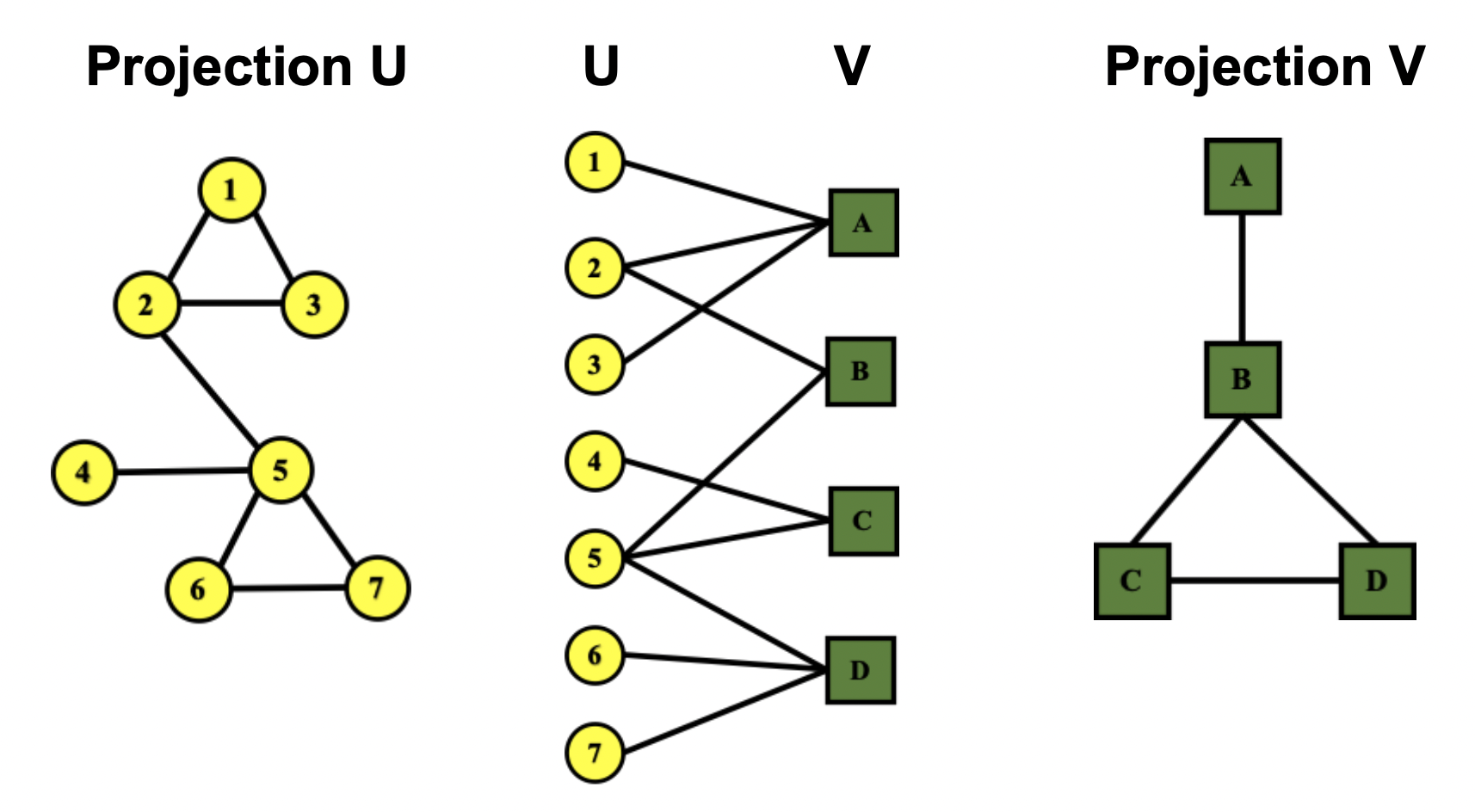
U-V 의 노드를 가지는 이분 그래프가 있다고 했을 때, 이를 Projection할 수 있음.
- Projection U : U노드가 1개 이상의 공통된 V와 연결되어 있으면 Projection graph U의 노드를 연결
- Ex) 이분 그래프의 1번, 2번 노드가 노드 A와 공통적으로 연결되어 있으므로 Projection U graph의 1번-2번 노드를 연결
- U가 저자, V가 논문이라면 Projection U graph는 한번이라도 같이 논문을 쓴 적 있는 사람들을 연결한 그래프가 된다.
- Projection V : V노드가 1개 이상의 공통된 U와 연결되어 있다면 Projection graph V의 노드를 연결
- Ex) 이분 그래프의 A, B 노드가 노드 2와 공통적으로 연결되어 있으므로 Projection V graph의 A-B 노드를 연결
- U가 저자, V가 논문이라면 Projection V graph는 같은 저자를 공유하는 논문을 연결한 그래프가 된다.
Representing Graphs
1) Adjacency Matrix
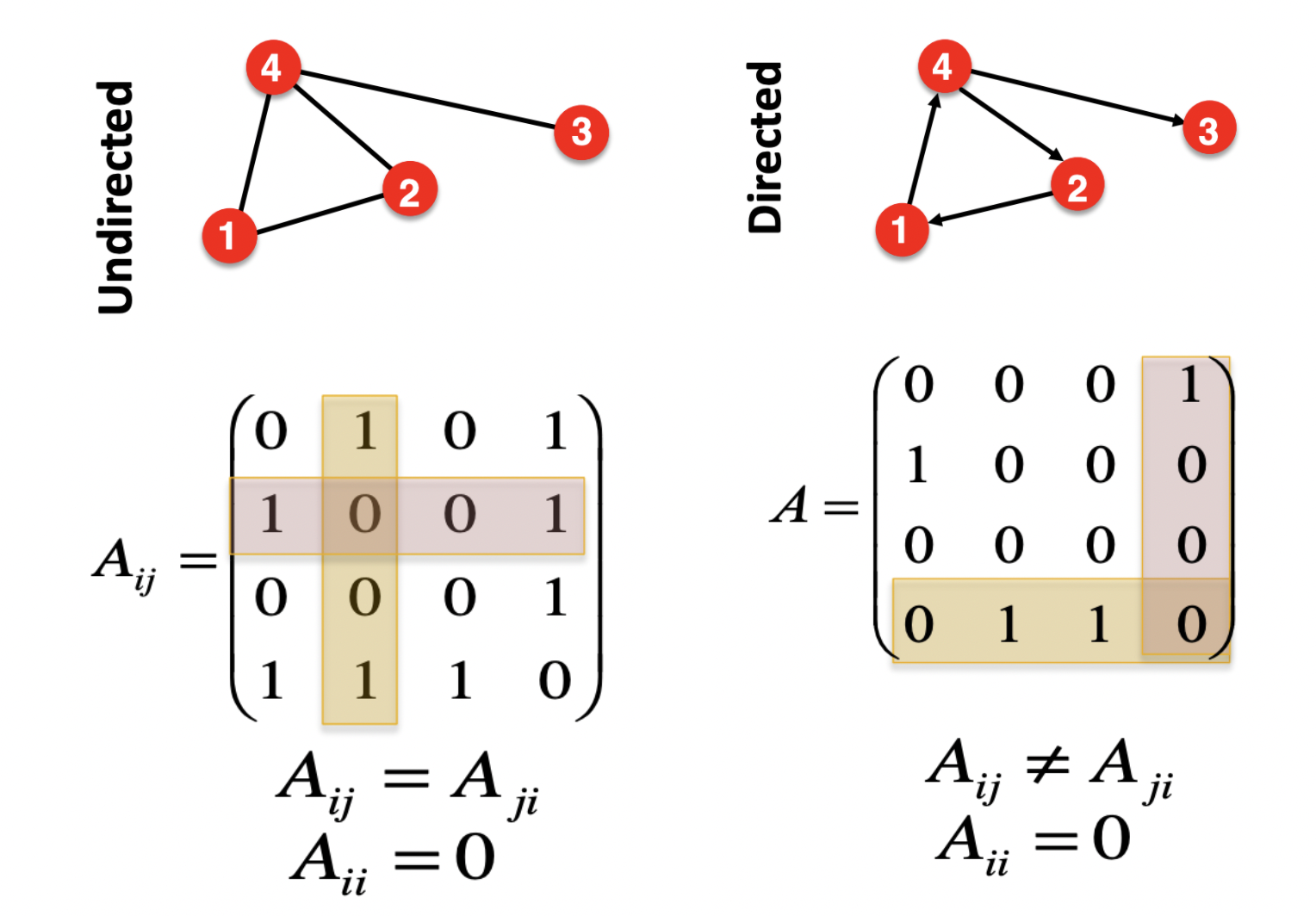
Undirected
- 방향성 없는 링크로 연결되어 있으므로,
i→j , j→i 로의 경로가 모두 존재한다고 생각
- 와 모두 1로 표시 - Symmetric (대칭적)
- 🟨 : =
- 🟥 : =
- 가로 sum = 세로 sum = degree
- 링크의 개수
Directed
- i → j 로 연결되어 있을 경우에 만 1로 표시
- Asymmetric (비대칭적)
- 🟨 : =
- 🟥 : =
- 가로 sum = out-degree
세로 sum = in-degree - 링크의 개수
⚠️ Most real-world networks are sparse
(= 한개의 노드가 최대로 가질 수 있는 엣지 수)
2) Edge list
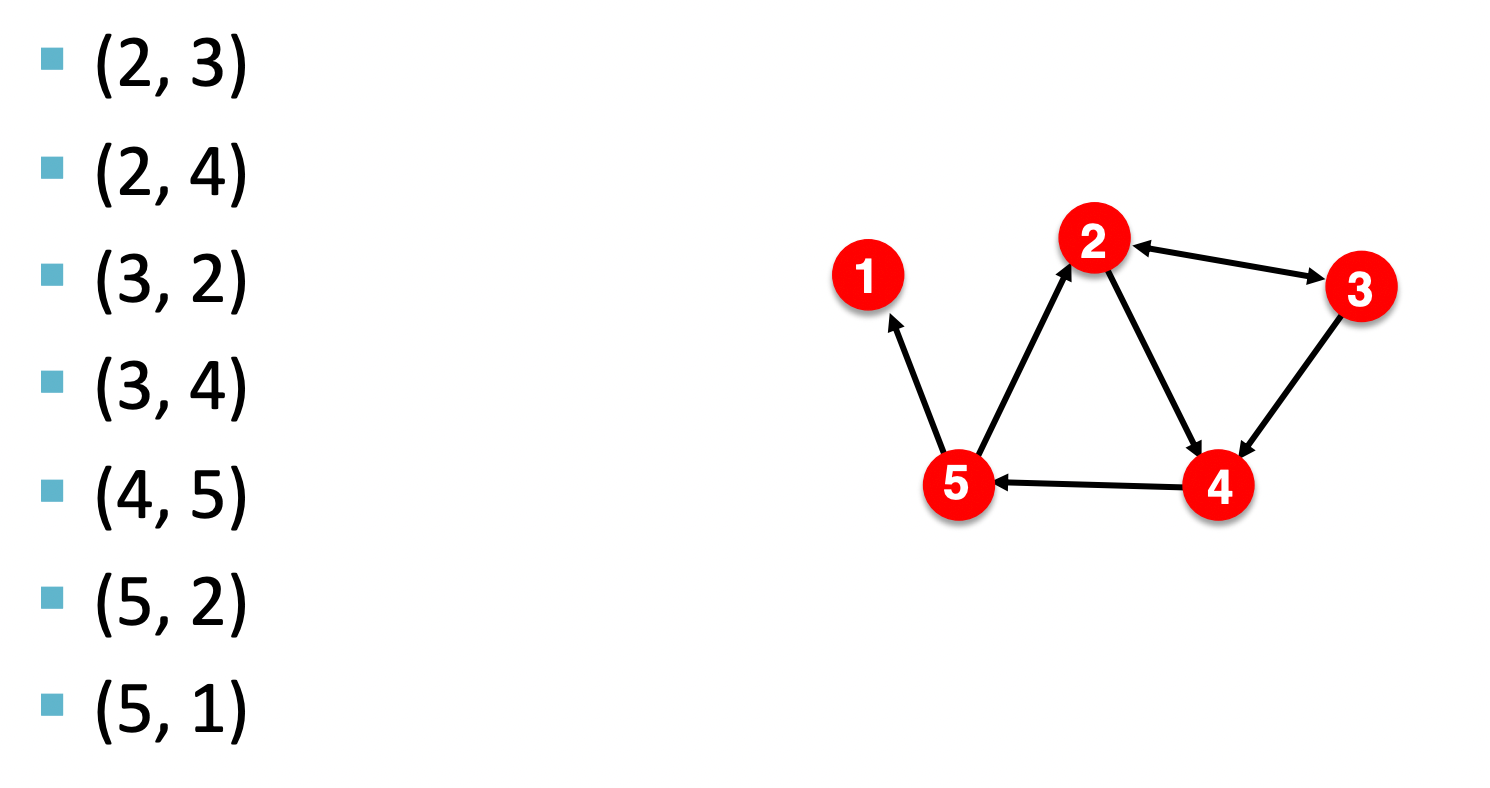
- 연결된 엣지를 2차원 리스트로 저장 → DL Framework에서 많이 쓰임 !
- Graph manipulation / analysis (조작 및 분석)이 어려움
- Ex) graph degree 계산이 어려움 등
⇒ 그래서 등장
3) Adjancency list

- Large & Sparse network를 다루기 용이
- 주어진 노드의 이웃을 빠르게 탐색 가능
cf > directed graph일땐 out-going과 in-going한 방향을 동시에 저장함.
More Types of Graphs
1) Unweighted vs. Weighted
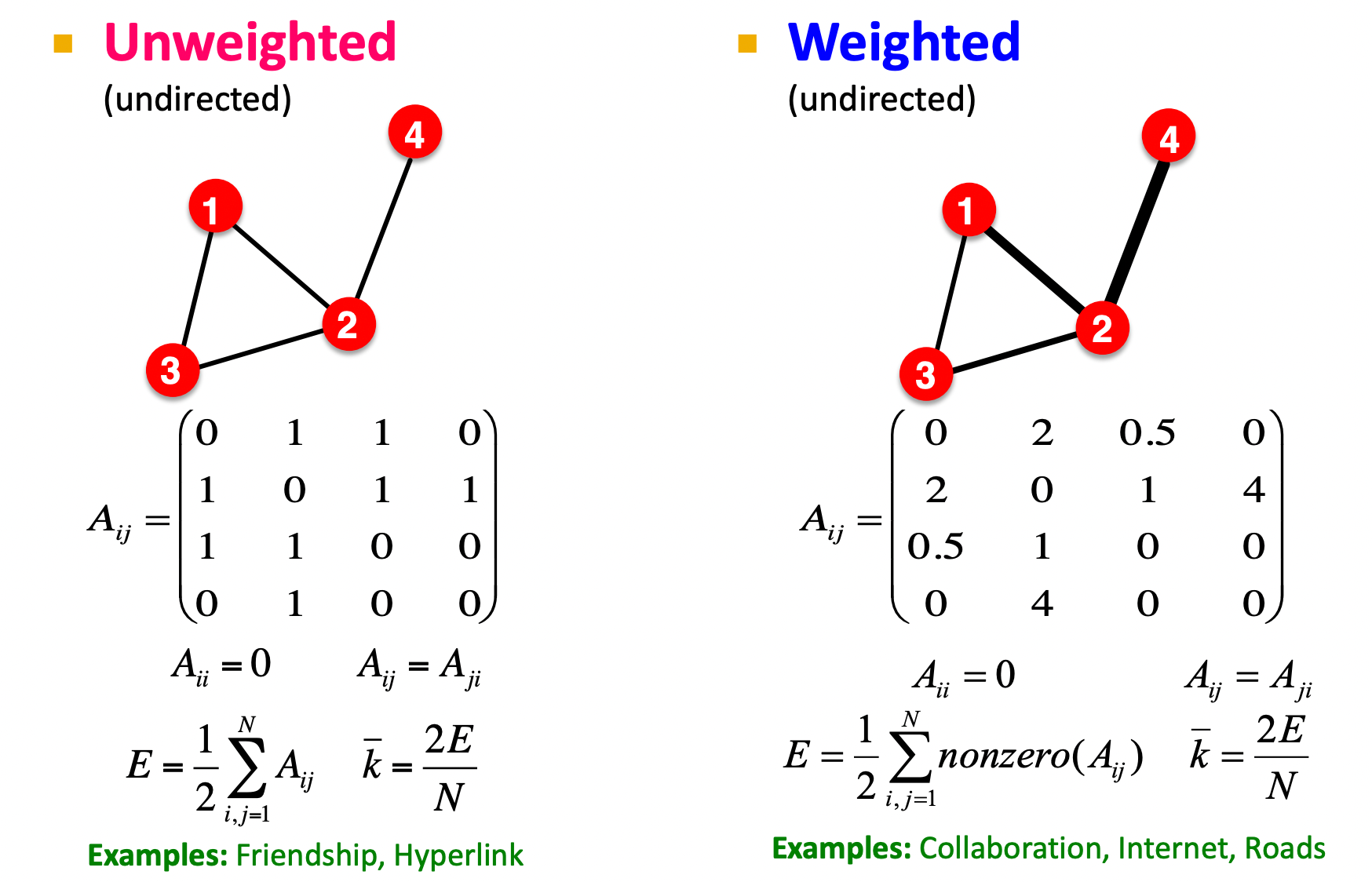
2) Self-edges (self-loops) & Multigraph
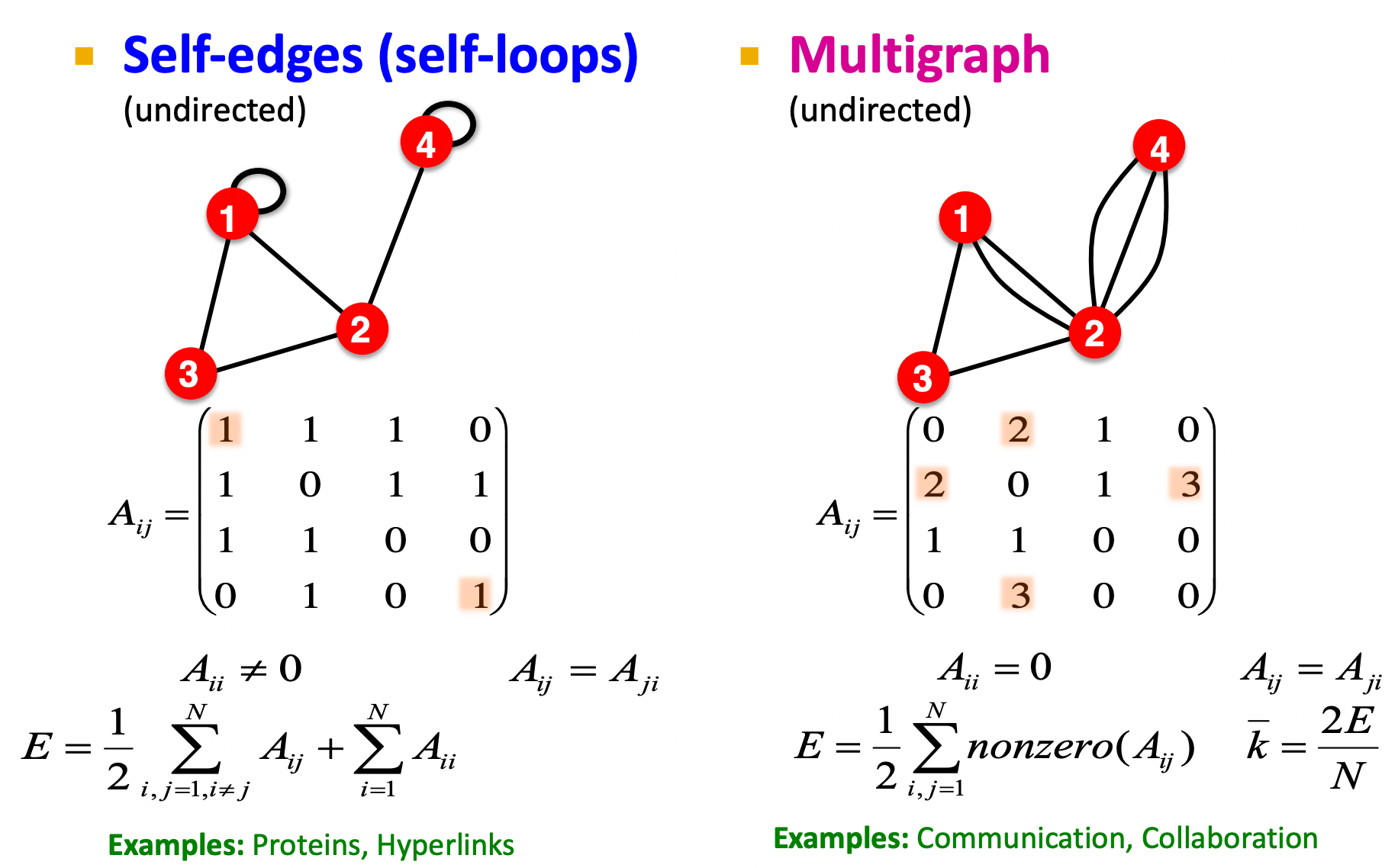
- matrix 대각선의 숫자가 0이 아님 = self-roof를 가짐을 의미
- node 4의 Degree = 3
- 가중치를 가지는 그래프와 비슷하게 표현됨
- weighted graph를 → multigraph로도 표현 가능
Notion of Connectivity
1. Undirected Graphs
Connected graph vs. Disconnected graph
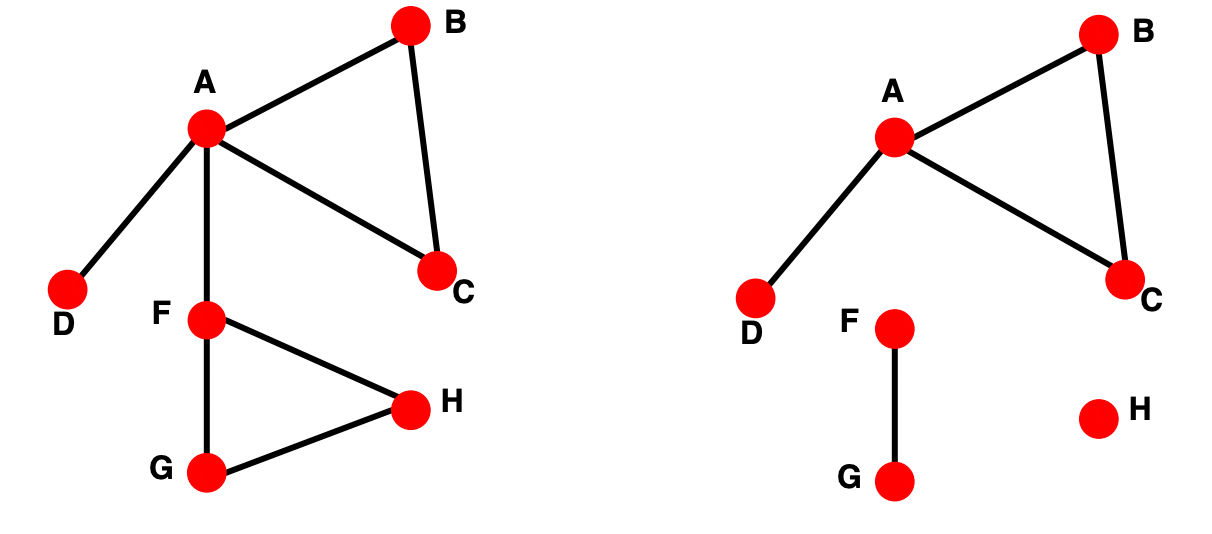
- Connected : 모든 노드가 서로 연결 가능
- Disconnected : 2개 이상의 연결 요소로 구성
- Largest Component: Giant Component
- Isolated node (ex. node
H)
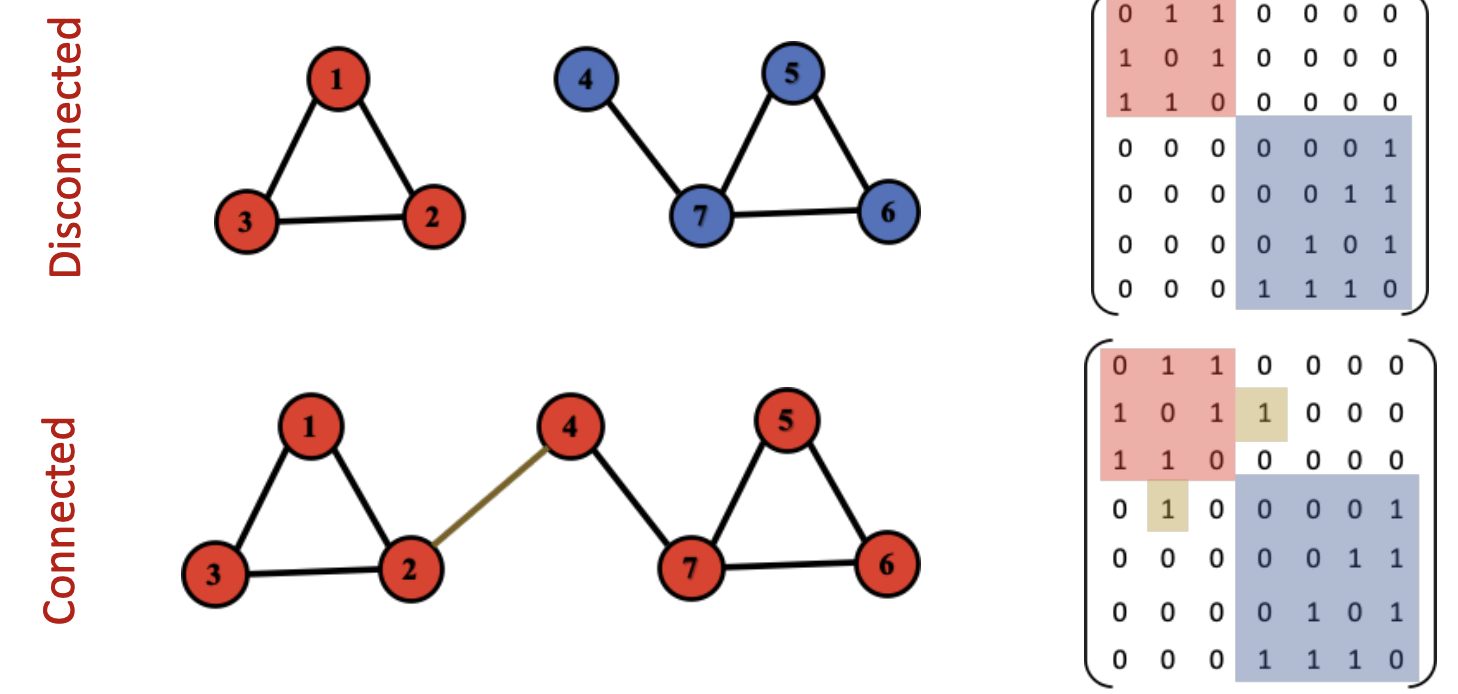
- Disconnected : 인접행렬이 대각선에 위치한 사각형 블록 형태로 나타남 → non-zero element가 블록 안에만 나타남
2. Directed Graphs
Strongly connected vs. Weakly connected
- 한 노드에서 다른 노드로 갈 수 있는 경로가 항상 존재함 → Strongly
- 방향을 무시하면 모두 연결되어 있음 But 일부 노드에서 다른 노드로 가는 경로가 존재하지 않음 → Weakly
Strongly connected components (SCCs)
: 강하게 연결된 연결된 노드의 집합 (방향 그래프의 부분집합)
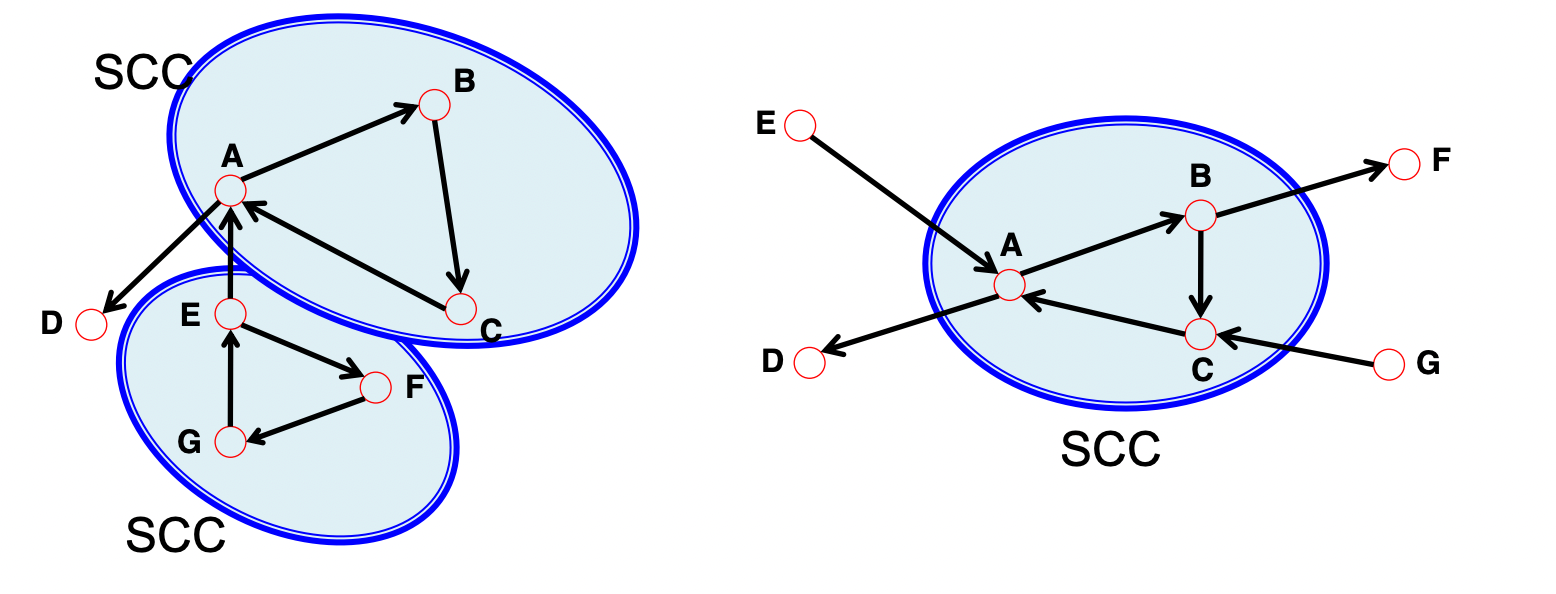
- In-component: nodes that can reach the SCC (ex. E of 2)
Out-component: nodes that can be reached from the SCC (ex. D of 2)
