DS School Week 9-4 통계 : 연속 확률 분포

오늘 학습 계획

• 통계 강의 수강 : 연속형 확률 분포

학습 내용

1. 연속 확률 분포 기초

• 확률 밀도 함수(PDF)
  • 정의
    • 모든 X에 대해서 $f(x) \ge 0$
    • $P(X \in(-\infin,\infin)) = \int_{-\infin}^\infin f(x) dx = 1$
    • $P(a \le X \le b) = \int_a^bf(x)dx$
  • 성질
    • $P(X=a) = P(a \le X \le a ) =\int_a^af(x)dx = 0$
    • $P(a \le X \le b) = P(a \le X < a ) = P(a < X \le a ) = P(a < X < a )$
  • $E(X) = \int_{-\infin}^\infin xf(x) dx$
    $Var(X) =E(X-\mu)^2 = \int_{-\infin}^\infin(x-\mu)^2f(x)dx$
• 누적 분포 함수(CDF)
  • 확률 밀도 함수를 적분하면 됨
  • $F(X) = P[X \le x] = \int_{-\infin}^xf(x)dt$
  • 성질
    • $0 \le F(X) \le 1$
    • $b \ge a$면, $F(b) \ge F(a)$
    • $F(b) - F(a) = P[a \le X \le b]$

2.균일 분포

• $f(x) = \begin{cases}{1 \over b-a}, \quad a \le x \le b \\ 0 , \quad otherwise\end{cases}$
• $f(x) = \begin{cases}0, \quad x \le a \\ {1 \over b-a}, \quad a \le x \le b \\ 1, \quad x\ge b \end{cases}$
• $E[X] = \int_a^b xf(x)dx = \int_a^bx{1 \over b-a}dx = [{1 \over b-a}{1 \over 2}x^2]_a^b = {b^2 - a^2 \over 2(b-a)} = {b+a \over 2}$
  $E[X^2] = \int_a^bx^2{1 \over b-a}dx ={b^2 + ab + a^2\over 3}$
  $Var[X] = E[X^2] - (E[X])^2 = {b^2 + ab + a^2 \over 3} - ({b + a\over 2})^2 = {(b-a)^2\over 12}$
  

3. 정규 분포

• $f(x) = {1 \over \sqrt {2\pi\sigma}} e^{- {1 \over 2 \sigma^2}(x-\mu)^2}, -\infin < x < \infin$
  $X \sim N(\mu, \sigma^2)$
• 엑셀 : norm.dist(x, μ, σ)
• 표준 정규 분포
• $X \sim N(\mu, \sigma^2)$일 때,
  $Z = {X - \mu\over \sigma} \Longrightarrow Z \sim N(0, 1)$
• $\phi(z) = {1 \over \sqrt{2 \pi}}e^{-{1\over 2}x^2}$
• 정규 분포의 성질
  • $X \sim N(\mu, \sigma ^2)$일 때, $aX+b \sim N(a\mu+b, a^2\sigma^2)$
  • $X \sim(\mu_1, \sigma_1^2), Y \sim N(\mu_2, \sigma_2 ^2)$이고 X와 Y가 독립일 때
    $aX+bY \sim N(a\mu_1+b\mu_2, a^2\sigma_1^2 + b^2\sigma_2^2. )$
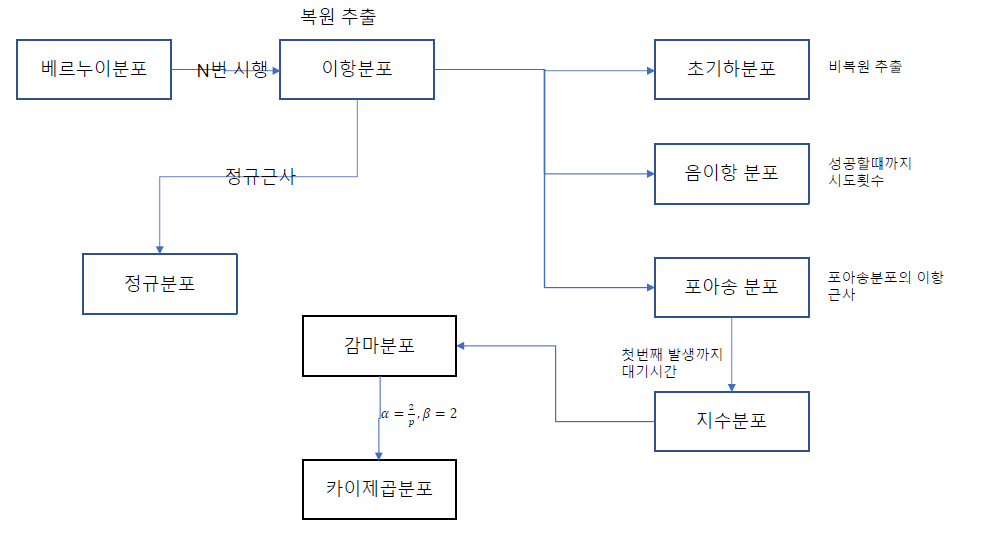
• 이항 분포의 정규 근사
  • $X \sim B(n, p)$일 때, 확률변수 X는 n이 충분히 크면 근사적으로 정규 분포 $X \sim N(np, np(1-p))$를 따름
  • $Z = {X-np \over \sqrt{np(1-p)}} \sim N(0,1)$

4. 지수 분포

• 단위 시간당 발생할 확률이 $lambda$인 어떤 사건의 횟수가 포아송 분포를 따를 때, 어떤 사건이 처음 발생할 때 가지 걸린 시간 확률 변수 X
• $X \sim Exp(\lambda)$
  $f(x) = \lambda e^{-\lambda x}, x \ge 0$
  → CDF : $F(x) = 1 - e ^{-\lambda x}, x \ge 0$
• $E[X] = {1 \over \lambda}$
  $Var[X] = {1 \over \lambda ^2}$
• 지수 분포의 무기억성
  • 어떤 시점부터 소요되는 시간은, 과거 시간에 영향을 받지 않음
  • $P(X>a+t | X > a) = P(X >t)$

※ 확률 분포의 관계

다음 학습 계획

• 통계 : 모집단과 표본 강의 수강