DS School Week 9-3 통계 : 이산 확률 분포

학습 계획

• 통계 : 데이터 강의 수강 (~이산 확률 분포)

학습 내용

1. 데이터

• 변수 : 조사 목적에 따라 관측된 자료값
  • 질적 변수 : 데이터를 범주로 구분할 수 있는 것
  • 양적 변수 : 이산형 변수(시험 점수 등) / 연속형 변수 (신장 등)
• EDA (Exploratory Data Analysis)
• 데이터 시각화
  • 시간시각화, 분포시각화, 관계시각화, 비교시각화, 공간시각화
• 데이터의 기초 통계량
  • 통계량이란? 표본으로 산출한 값 (= 기술 통계량)
  • 중심경향치
    • 평균
      • 표뵨 평균 : $\bar x$
      • 모평균 : $\mu$
    • 중앙값(median)
      $m =\begin{cases}x_{(k+1)}&, n = 2k+1 \\\frac{(x_{(k)} + x_{(k+1)})}{2}, & n=2k \end{cases}$
    • 최빈값
  • 산포도
    • 범위 : 데터의 최대값과 최소값의 차이
    • 사분위수 : 전체 데이터를 오름차순하여 4등분 하여 제1사분위수(Q1) ~ 제3사분위수(Q3)이라고 함.
      $\quad\quad\quad$ 사분위수범위 : IQR = Q3 - Q1
    • 백분위수(percentile)
      전체 데이터를 오름차순하여 주어진 비율에 의해 등분한 값.
      제p백분위수 : p%에 위치한 자료 값.
      자료가 n개가 있을 때, 제(100*p) 번째 백분위 수
      • np = 정수 : np번째와 (np+1)번째 자료의 평균
        np ≠ 정수 : np보다 큰 최소 정수 m번째 자료
    • 분산
      표본분산
      s$^2 = {1 \over n-1} \sum_{i=1}^n(x_i - \bar x)^2$
      모분산 (모집단 크기 N일때)
      $\sigma ^2 = {1 \over N}\sum_{i=1}^N(x_i - \mu)^2$
    • 표준 편차
      표본 표준편차 : $s = \sqrt{s^2}$
      모 표준편차 : $\sigma = \sqrt{\sigma^2}$
    • 변동계수(Coefficient of Variation : CV)
      평균이 다른 두개 이상의 그룹의 표준편차를 비교
      $cv = {s \over \bar x}$
  • 왜도(skew)
    자료가 얼마나 배디청직인지 표현하는 지표
    0에서 클수록 우측 꼬리가 길고, 0에서 작을수록 좌측 꼬리가 김.
  • 첨도(kurtosis)
    3에 가까울 수록 정규 분포에 가까움
    k < 3 인 경우 정규분포보다 꼬리가 얇음
    k > 3 인 경우 정규분포보다 꼬리가 두꺼움

2. 확률 이론

• 확률이론
  • 확률의 개념
    • 확률 : 모든 경우의 수에 대한 특정 사건이 발생하는 비율
    • 표본 공간(S) : 실험에서 나올 수 있는 모든 결과들의 집합
    • 사건 A가 일어날 확률
      $P(A) ={사건A가\space일어날\space원소의\space수\over표본공간S의\space원소의\space수}$
  • 확률의 성질
    • 합사건 : 사건 A 또는 B가 일어날 확률
      $A\cup B$
    • 곱사건 : 사건 A 와 B가 동시에 일어날 확률
      $A\cap B$
    • 배반사건 : 사건 A와 B가 동시에 일어날 수 없을 경우
      $A\cap B = \empty$
      $P(A \cap B) = P(\empty) = 0$
    • 여사건 : 사건 A가 일어나지 않을 확률
      $A^c$
      $P(A) + P(A^c) = 1$
    • 확률의 덧셈 법칙
      $P(A \cup B) = P(A) + P(B) - P(A \cap B)$
  • 순열과 조합
    • 순열 : 순서를 고려하여 n개 중 r개를 뽑아서 배열하는 경우의 수
      $_nP_r = {n!\over(n-r)!}$
    • 조합 : 순서를 고려하지 않고 n개 중 r개를 뽑아서 배열하는 경우의 수
      $_nC_r = {nP_r\over r!} = {n! \over r!(n-r)!}$
  • 조건부 확률

    • 어떤 사건 A가 발생한 상황에서 또 하나의 사건 B가 발생한 확률
      $P(B|A) = {P(A \cap B) \over {P(A)}}, P(A) \ne 0$

    • 확률의 곱셈 법칙
      $P(A \cap B)= P(A)\cdot\ P(B|A) = P(B)\cdot P(A|B)$
      사건 A와 B가 독립일 경우, $P(A \cap B)= P(A)P(B)$

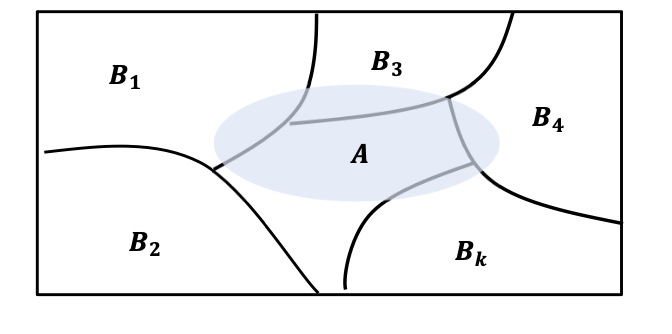
    • 베이즈 정리
      표본 공간 S에서 서로 배반인 사건 $B_1, B_2, ..., B_k$에 의하여 분할 되어 있을 때, 임의의 사건 A에 대하여 성립하는 정리
      $P(A|B) = {P(B|A)P(A)\over P(B)}$
      * P(A) : 사전 확률
      * P(A|B) : 사후 확률
      * P(B|A) : 가능도

      $P(B_i|A) = {P(B_i \cap A) \over P(A)} = {P(A|B_i)\times P(B_i) \over \sum_{j=1}^kP(A|B_j) \times P(B_j)}$
      

3. 확률 변수

• 확률 변수 : 표본 공간에서 각 사건에 실수를 대응 시키는 함수

  • 확률 변수는 X, 확률 변수의 특정 값은 x로 표현한다.
  • 이산 확률 변수 / 연속 확률 변수가 있다.

• 확률 변수의 평균(기대값)
  $E(X) = \sum_{i=1}^nx_iP(x_i)$

  기대값의 성질 * a, b가 상수일 때

  • $E(a) = a$
  • $E(aX) = aE(X)$
  • $E(aX+b) = aE(X) + b$
  • X, Y가 독립일 때 $\quad E(XY) = E(X)E(Y)$

• 확률 변수의 분산
  $Var(X) = {1 \over N} \sum(x_i - \mu)^2$
  분산의 성질 * a, b가 상수일 때

  • $Var(a) = 0$
  • $Var(aX) = a^2Var(X)$
  • $Var(X+Y) = Var(X) + Var(Y) + 2Cov(X, Y)$
  • X, Y가 독립일 때 $\quad Var(XY) = 0$
  • $Var(X) = E(X^2) - [E(X)]^2$

• 공분산 : 2개의 확률변수의 선형관계를 나타내는 값
  $\begin{matrix}Cov(X,Y) =E[(X-E(X)))(Y-E(Y))] \\ ={\sum_i^n(X_i-\bar X)(Y_i - \bar Y) \over n-1} \end{matrix}$

4. 확률 분포

• 확률 분포 : 확률 변수 X가 취할수 있는 모든 값과 그 값을 나타날 확률을 표현하는 함수

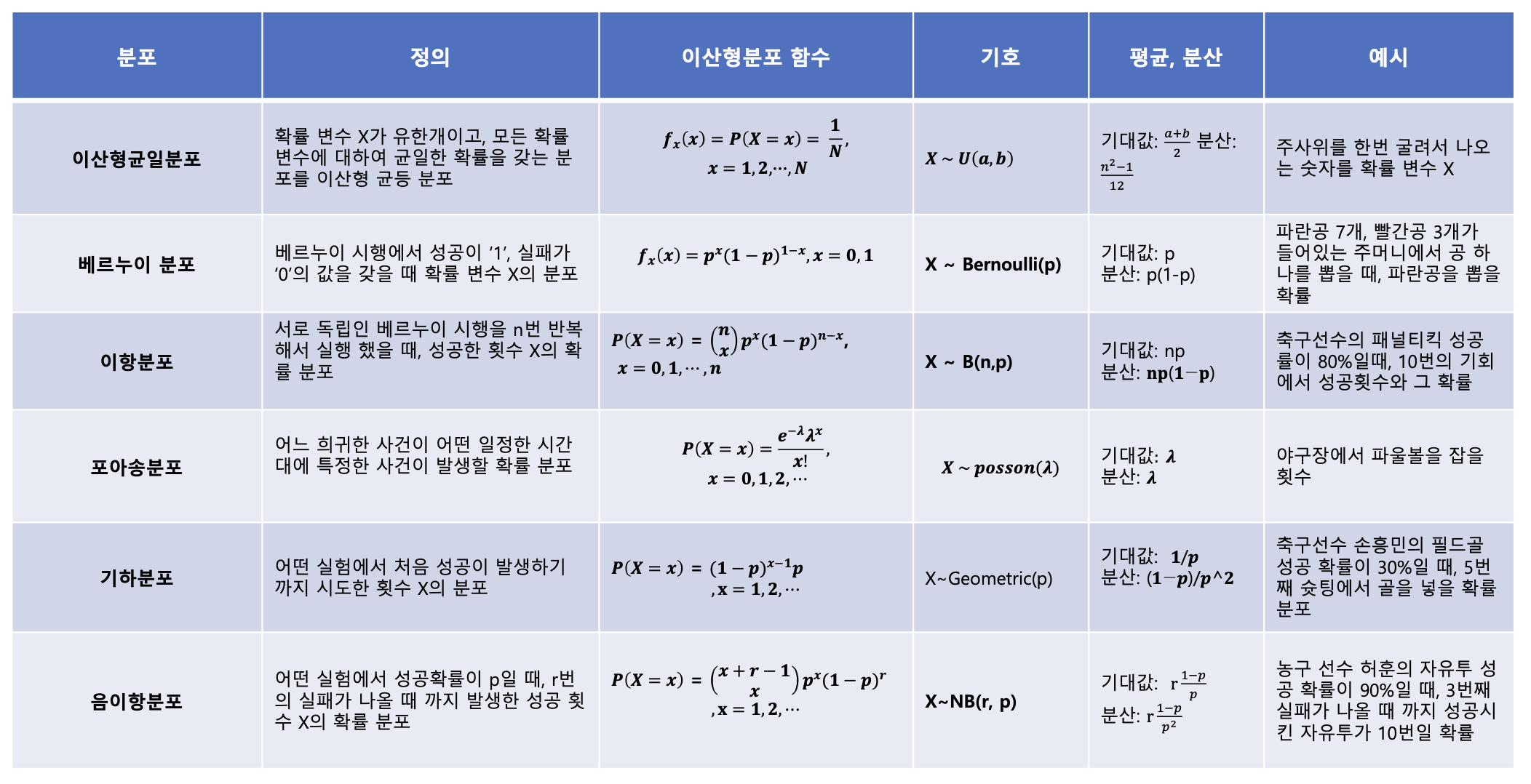
• 이산 확률 분포

  • 이산형 균등 분포
    • 모든 확률 변수에 대하여 균일한 확률을 갖는 분포
    • $f_x(x) = P(X=x) = {1 \over N}$
      $X \sim U(a,b)$
    • 예) 주사위를 굴려서 나오는 숫자 X
    • $E[X] = \sum xf(x) = {1 \over n} * {n(n+1) \over 2}$
      $Var[X] = E(X^2) - E[X]^2 = {(N+1)(2N+1) \over 6} - ({N+1 \over 2 })^2 = {(N+1)(N-1)\over 12}$
      * $E(X^2) = {\sum x^2f(x) = {1 \over n}\sum x^2} = {(N+1)(2N+1) \over 6}$
  • 베르누이 분포
    • 베르누이 시행 : 각 시행의 결과가 성공, 실패 두가지 결과만 존재하는 시행
    • $X = \begin{cases}1 성공 \\ 0 실패 \end{cases}$
      $X \sim Bernoulli(p)$
      $f_x(x) = p^x(1-p)^{1-x}$
    • $E[X] = 1 \cdot p + 0 \cdot (1-p) = p$
      $Var[X] =\sum x^2f(x) - p^2 = p - p^2 = p(1-p)$
  • 이항분포
    • 서로 독립인 베르누이 시행을 n번 반복해서 실행했을때, 성공한 횟수 X의 분포
    • $f_x(x) = P(X=x) = \begin{pmatrix}n \\ x\end{pmatrix}p^x(1-p)^{n-x} = {n!\over x!(n-x)!}p^x(1-p)^{n-x}$
      $X \sim B(n,p)$
    • 예) 축구 선수가 10번의 패널티킥을 시도할 때 성공 횟수와 그 확률
      공장에서 불량이 n개 발생할 확률
    • $E[X] = \sum xf(x) = \sum_{r=0}^nr\cdot _nC_rp^rq^{n-r}$
      $\quad\quad\quad=\sum_{r=0}^nr\cdot _{n!\over(n-r)!r!)}p^rq^{n-r} \ =\sum_{r=1}^n{n(n-1)!\over(n-r)!(r-1)!}p\cdot p^{r-1}q^{n-r}$
      $\quad\quad\quad = np\sum_{r=1}^n \ _{n-1}C_{r-1}p^{r-1}q^{(n-1)-(r-1)} = np$
      $Var[X] = n(n-1)p^2 + np - (np)^2 = np(1-p)$
      $\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad = npq$
  • 포아송 분포
    • 어느 흐귀한 사건이 어떤 일정한 시간대에 발생할 확률 분포
      • 어떤 단위구간 동안 이를 더 짧은 단위구간으로 나눌 수 있고,
        짧은 단위 구간 중 어떤 사건이 발생할 확률은 전체 중 항사 일정
      • 두 개 이상의 사건이 동시에 발생할 확률 0
      • 어떤 단위구간의 사건 발생은 다른 단위구간의 발생으로부터 독립적임
      • 특정 구간에서의 사건 발생확률은 그 구간의 크기에 비례함
    • 예) 야구장에서 파울볼을 잡을 횟수
      버스 정류장에서 특정 버스가 5분 이내 도착한 횟수
      1년간 지구에 1미터 이상의 운석이 떨어지는 수
    • $f_x(x) = {e^{- \lambda} \lambda ^x\over x!}$
      $X \sim posson(\lambda)$
    • $E[X] = \lambda$
      $Var[X] = \lambda$
  • 이항분포의 포아송 근사
    • 확률변수 X가 $X \sim B(n,p)$이고, n이 충분히 크고(n≧30), p가 아주 작을 때 X의 분포는 평균이 $\lambda = np$인 포아송 분포로 근사시킬 수 있음
      $X \sim Poisson(np)$
      * np < 5를 만족하면 근사 정도가 좋다고 함
  • 기하 분포
    • 어떤 실험에서 처음 성공이 발생하기 까지 시도한 횟수 X의 분포. 이 때 각 시도는 베르누이 시행을 따름.
    • $f_x(x) = (1-p)^{x-1}p$
      $X \sim Geometric(p)$
    • 예) 축구선수가 n번째 슛팅에서 골을 넣을 확률
    • $E[X] = {1 \over p}$
      $Var[X] = {1-p \over p^2}$
  • 음이항 분포
    • 어떤 실험에서 성공확률이 p일 때, r번의 실패가 나올때 까지 발생한 성공횟수 X의 확률 분포
    • $f_x(x) = _{x+r-1}C_xp^x(1-p)^r$
      $X \sim NB(r,p)$
    • 예) 농구선수가 r번째 실패가 나올 때 까지 성공시킨 자유투 수가 x번일 확률
    • $E[X] = r {1-p \over p}$
      $Var[X] = r {1-p \over p^2}$

  

다음 학습 계획

• 통계 강의 수강 : 연속형 확률 분포