프로그래머스: 약수의 개수와 덧셈

(문제링크)

문제

두 정수 left와 right가 매개변수로 주어집니다.
left부터 right까지의 모든 수들 중에서, 약수의 개수가 짝수인 수는 더하고, 약수의 개수가 홀수인 수는 뺀 수를 return 하도록 solution 함수를 완성해주세요.

제한사항

• 1 ≤ left ≤ right ≤ 1,000

입출력 예

left	right	result
13	17	43
24	27	52

입출력 예 설명

입출력 예 #1
다음 표는 13부터 17까지의 수들의 약수를 모두 나타낸 것입니다.

수	약수	약수의 개수
13	1, 13	2
14	1, 2, 7, 14	4
15	1, 3, 5, 15	4
16	1, 2, 4, 8, 16	5
17	1, 17	2

• 따라서, 13 + 14 + 15 - 16 + 17 = 43을 return 해야 합니다.

입출력 예 #2
다음 표는 24부터 27까지의 수들의 약수를 모두 나타낸 것입니다.

수	약수	약수의 개수
24	1, 2, 3, 4, 6, 8, 12, 24	8
25	1, 5, 25	3
26	1, 2, 13, 26	4
27	1, 3, 9, 27	4

• 따라서, 24 - 25 + 26 + 27 = 52를 return 해야 합니다.

첫번째 풀이

left 와 right 사이의 숫자들의 약수의 개수를 구한 뒤,
약수가 짝수개라면 더하고, 약수가 홀수개라면 빼줬다.

소스코드

function solution(left, right) {
    let answer = 0;
    
    for (let i=left; i<=right; i++) {
        let divisorCnt = 0;
        
        // 약수의 개수 구하기
        for (let j=1; j<=i; j++) if (i%j === 0) divisorCnt++;
        
        // 약수가 짝수라면 더하고, 홀수라면 빼주기
        if (divisorCnt%2 === 0) answer += i;
        else answer -= i;
    }
    
    return answer;
}

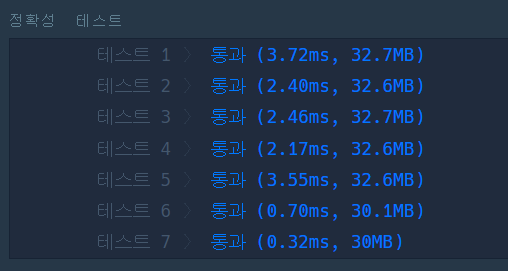
테스트 결과

두번째 풀이

만약, 한 가지 사실을 안다면 훨씬 간결하게 풀 수 있다.

$x$가 자연수의 제곱이라면, 약수의 개수는 홀수
$x$가 자연수의 제곱이 아니라면, 약수의 개수는 짝수

약수의 개수를 구하기 위해 반복문을 사용할 필요없이 자연수의 제곱인지 아닌지 판별하면 되기 때문에 실행 속도가 더 빨라진다.

function solution(left, right) {
    let answer = 0;
    
    for (let i=left; i<=right; i++) {
        // 자연수의 제곱이라면 약수의 개수는 홀수
        //   짝수라면 더하고 홀수라면 빼주기
        if (Math.sqrt(i)%1 === 0) answer -= i;
        else answer += i;
    }
    
    return answer;
}

위에서는 조건문을 Math.sqrt(i)%1 === 0 로 해서 1로 나눈후 나머지가 0인지 아닌지로 판단하는데,
Number.isInteger(Math.sqrt(i)) 로 나머지가 있는지 아닌지 판단하는 방법도 있다.

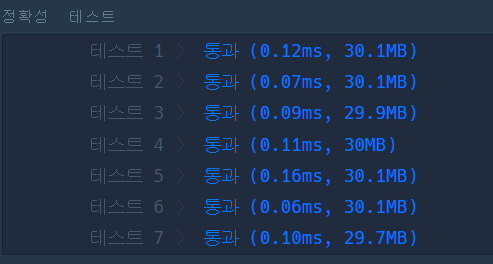
테스트 결과

느낀 점

수학에 대해 잘 알수록, 시간 효율을 높일 수 있는 것 같다.
나중에 시간이 된다면 수학을 다시 공부해보고 싶다 !