논문링크

Summary

• DDPM에서 발전된 논문 DDIM
• DDPM은 Markov Chain Process를 통해 noise를 제거하는 과정을 거침.
• 위 과정은 timestep 마다 이루어져야하므로 매우 많은 step이 필요함.
• 한 step 만에 끝나는 GAN에 비해 속도가 매우 느림.
• DDIM은 Non-Markov Chain Process를 통해 sampling 과정을 단순화 시켜 빠르게 동작하도록 함.

Method

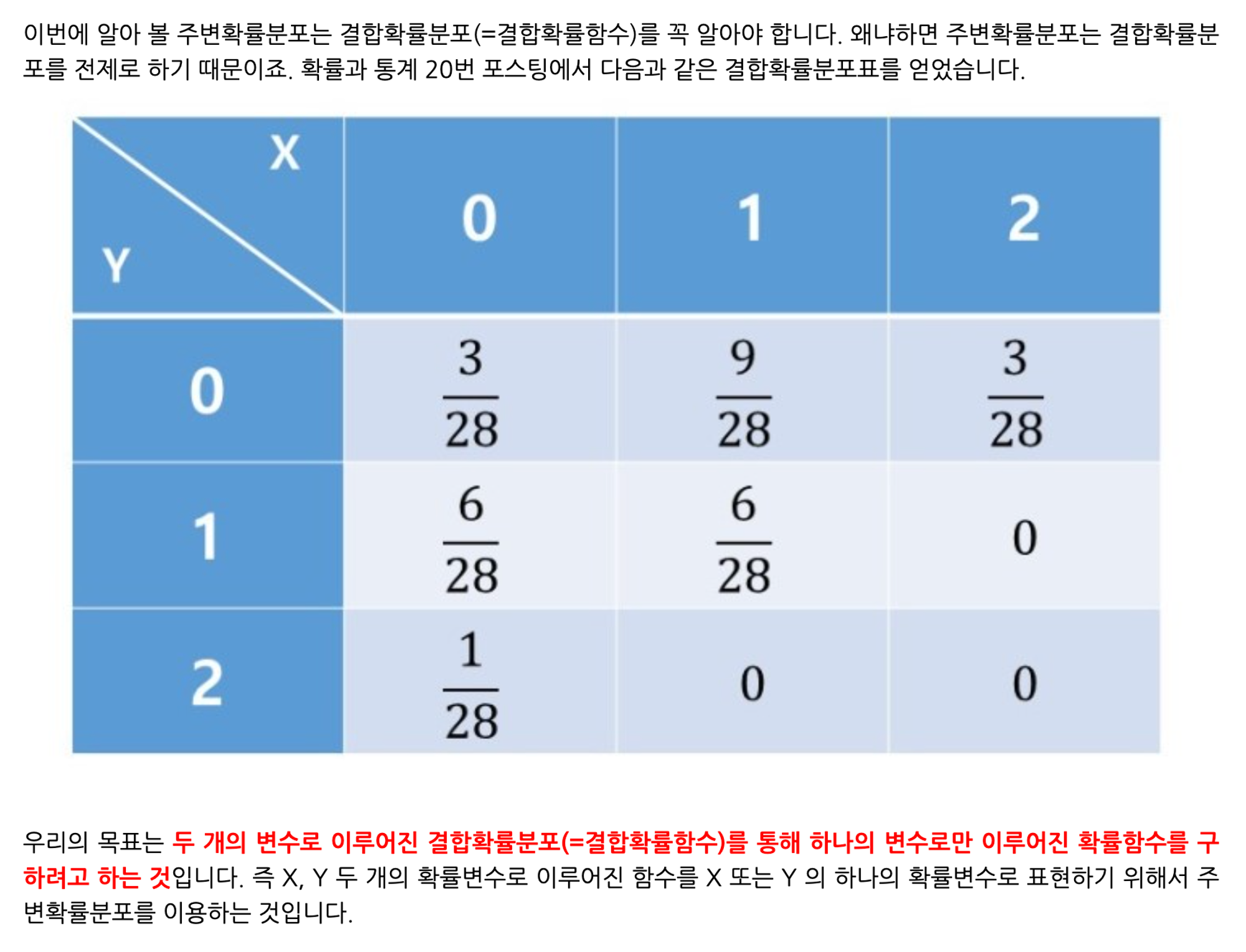
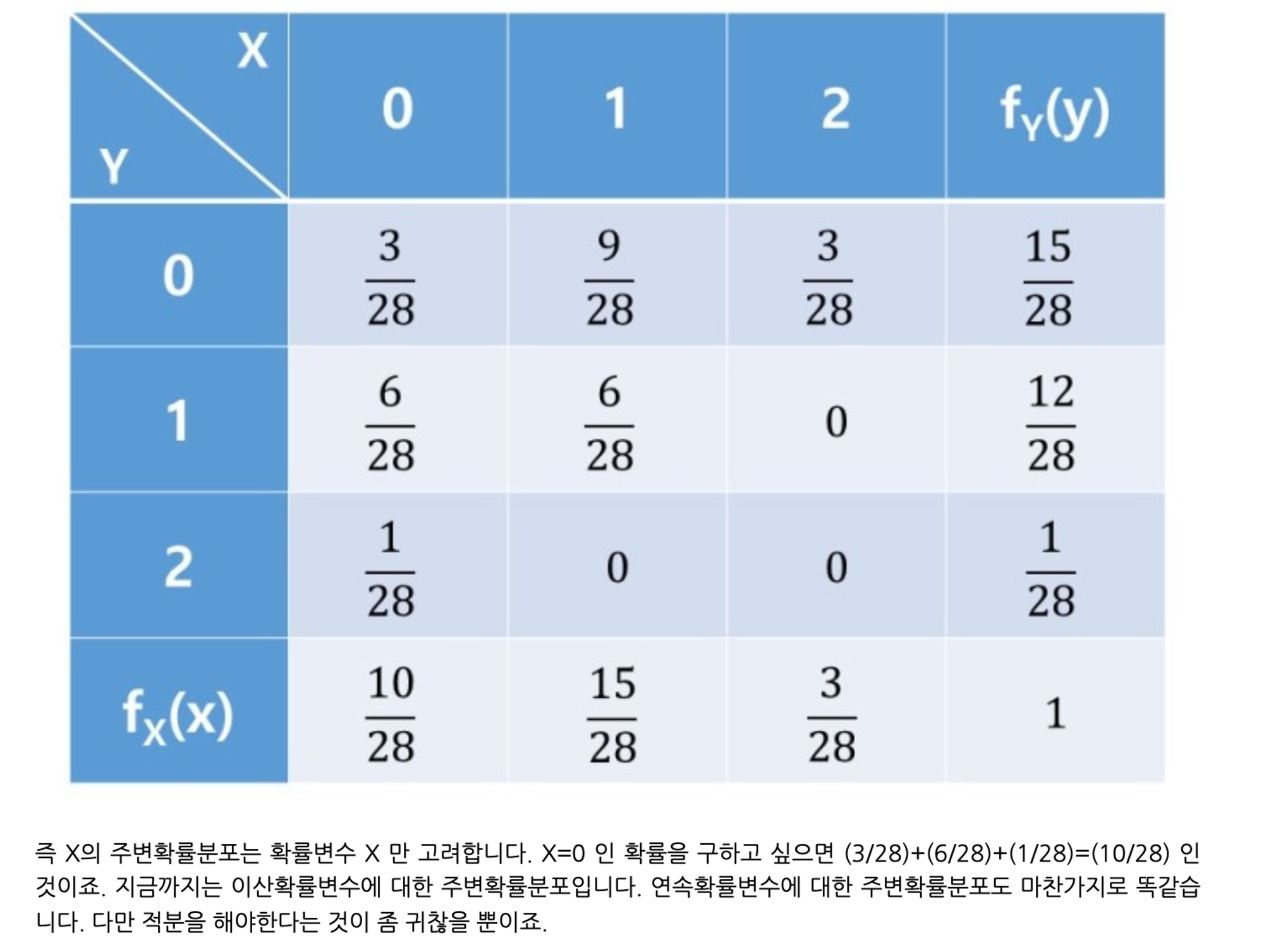
• DDPM의 $L_r$이 marginal distribution($q(x_t|x_0)$)에만 의존하고, joint distribution($q(x_{1:T}|x_0)$)에는 직접적으로 의존하지 않음을 발견.

marginal distribution(주변분포) & joint distribution(결합분포)

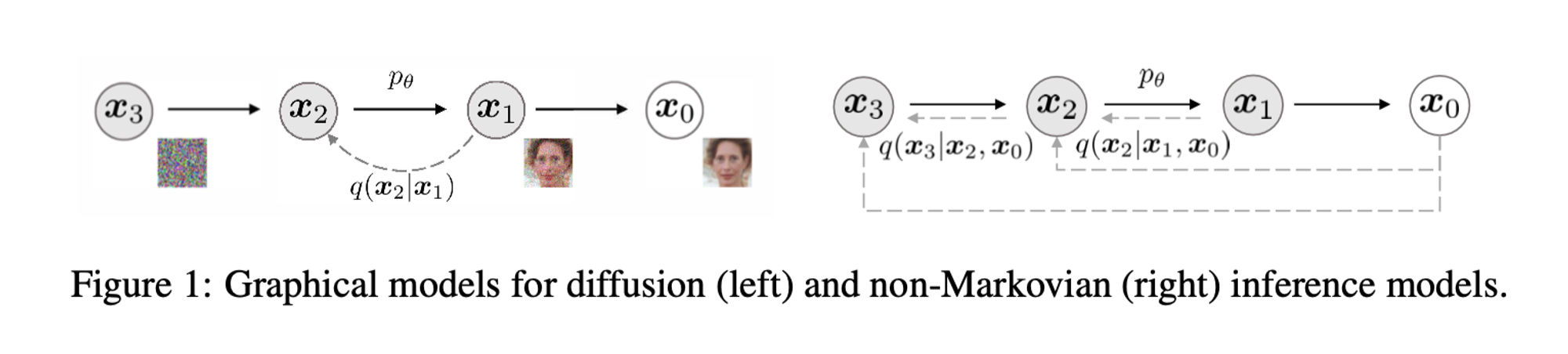
Non-Markovian Forward Process

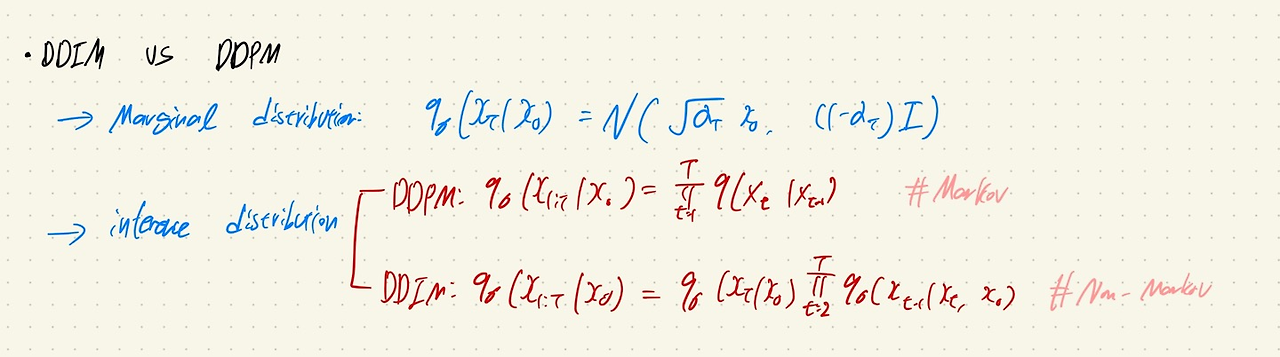
DDPM과 DDIM의 Marginal Distribution은 동일하지만, Joint Distribution의 식이 non-markovian으로 표현된다는 점이 다름.
즉, DDPM에서는 $x_t$가 $x_{t-1}$에 의해서만 결정되었다면, DDIM에서는 $x_t$와 $x_0$를 이용해서 $x_{t-1}$을 결정.

이를 베이지안으로 표현하면,

$\sigma$는 모델의 stochastic 정도를 나타냄.
모든 $t$에 대해 $\sigma_t=0$이면, forward process는 deterministic해짐. 이 경우 $x_T$부터 $x_0$까지 모두 고정되어 샘플링되므로, 모델이 implicit probablistic model이 됨. -> DDIM

Generative Process

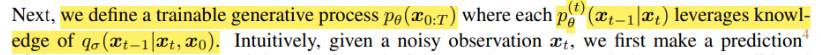
q 분포의 값을 토대로 p 분포를 학습함.
즉, $x_{t-1}$은 noise 한 $x_t$가 있을 때 $x_0$를 이용해서 $x_{t-1}$을 sampling하는 방식.

t=1일때는 gaussian noise를 더해줌. 이는 논문에서 generative process가 어디에서나 잘 supported할 수 있도록 ensure한다고 함.
이 외의 경우는 $f(x_t)$와 $x_t$를 이용해서 $x_{t-1}$을 sampling함.
($f(x_t)$는 어떠한 $x_t$에 대해서 $x_0$를 예측하는 함수)

Sampling From Generalized Generative Processes

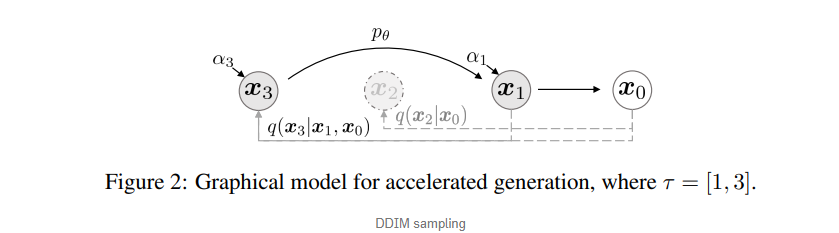
Denoising Diffusion Implicit Models

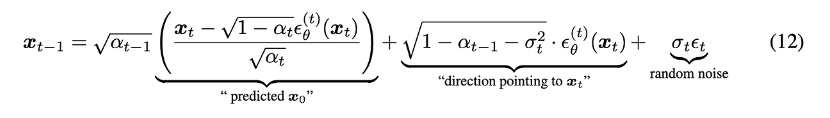
논문의 sampling 과정에 대한 설명
1. 위에서 정의된 generative process와 기존에 정의되어 있던 forward process의 수식을 바탕으로 $X_{t-1}$이 sampling되는 과정을 적을 수 있음.
2. 만약 sigma가 0이 아니라면, markovian이 되므로 이는 DDPM과 동일
3. sigma가 0이라면, random noise가 0이 되기 때문에 $X_T$에서 $X_0$로 sampling되는 과정이 고정됨.

**발췌

Acclerated Genertaion Processes

Forward process가 T steps를 가지고 있다고 해도, L1까지 가는 sampling 과정에서 더이상 특정한 forward 과정을 고려하지 않아도 되므로, 더 적은 step으로 충분히 generation할 수 있음. ($q_{\sigma}(x_t|x_0)$가 고정)

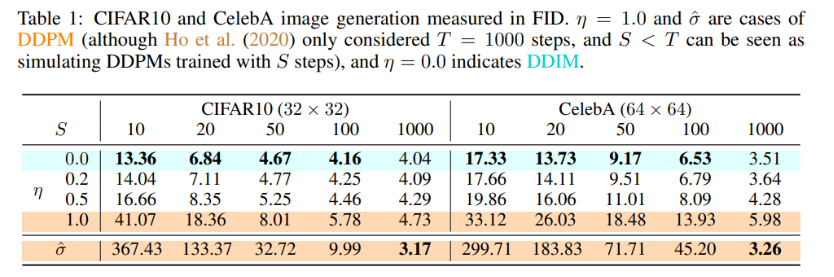
Result