[논문 리뷰] Denoising Diffusion Probabilistic Models

논문 링크

Summary

DDPM 전에, Diffusion 모델을 한 문장으로 요약하면?

데이터에 점진적으로 노이즈를 추가하고, 이를 반대로 제거하는 과정을 통해 고차원 데이터의 분포를 효과적으로 학습하고 새로운 데이터를 생성할 수 있는 확률적 생성 모델.

결국 그래서, DDPM이 무엇인가?

1. Diffusion 모델의 일종.
2. 기존 diffusion 모델의 loss term과 parameter estimation 과정을 더 학습이 잘 되는 방향으로 발전시킨 논문.

먼저, Diffusion Model

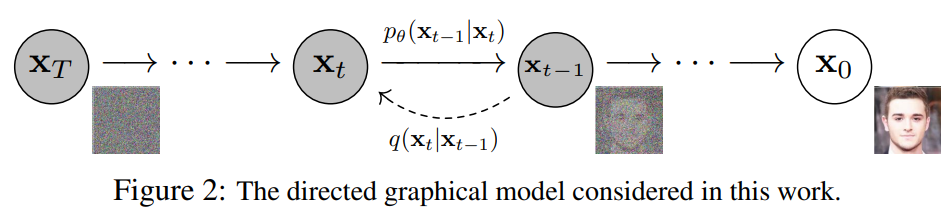
1. Forward diffusion process

• 데이터에 점차 noise를 추가해과는 과정.
• $q(x_{1:T}|x_0)$

2. Reverse diffusion process

• 데이터에서 noise를 점차 걷어내는 과정.
• $p_{\theta}(x_{0:T}|x_T)$

3. Loss func

• 다른 생성 모델들처럼, 실제 데이터의 확률분포 $p_{data}(x_0)$ 를 학습하는 것을 목표로 한다.

이에 따라, 아래의 Loss를 minimize하는 방향으로 학습이 진행된다.

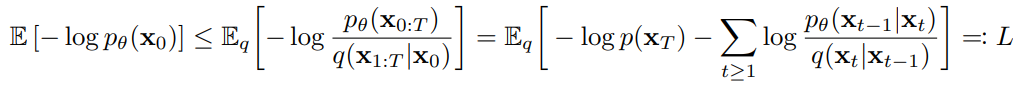
위 Loss를 normal disturibution 사이의 KL divergence 형태로 표현하면 아래와 같다.

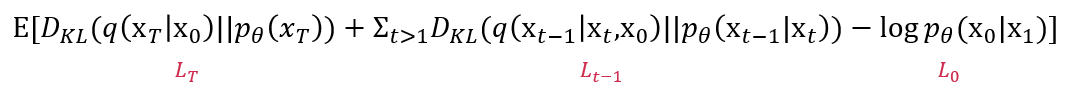
note: KL divergence를 모름. 다시 이해하려 해봐야할 듯

이제, DDPM

1. Forward process

• DDPM의 forward process는 기본적인 diffusion 모델과 같이 데이터에 "가우시안 노이즈"를 더하는 형태로 정의된다.
  forward process는 아래와 같이 진행된다.
  
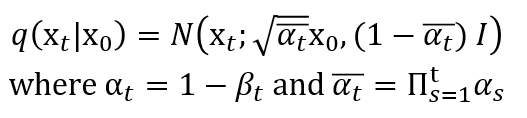
  이때, $\beta_t$는 DDPM에서 미리 정해진 상수이다.

  We set the forward process variances to constants increasing linearly from β1 = 10−4 to βT = 0.02. (4절 Experiment, 5p.)

그러므로 forward process는 별도의 학습이 필요하지 않다.

2. Reverse process

아래는 diffusion 모델의 reverse process 이다.

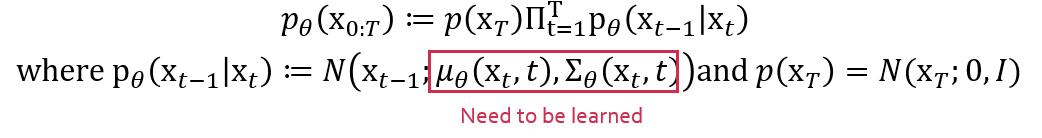
DDPM에서 우리는 $\mu_{\theta}$ 와 $\sum_{\theta}$ 를 학습해야한다.

3. Loss function

DDPM 또한 diffusion 모델의 일종이므로 아래와 같은 loss function을 최소화 하는 것을 목적으로 한다.

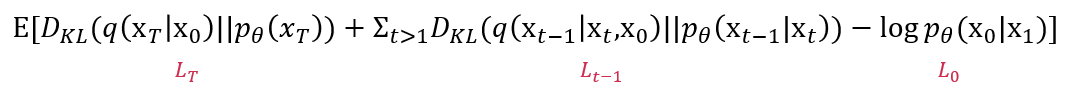
이제, DDPM에서 각 항을 어떻게 최소화하는지를 보자.

$L_T$

위에서 forward process는 학습이 필요하지 않다고 가정했다. 그러므로 이는 상수항에 해당한다.

$L_{t-1}$

$L_{t-1}$을 계산하기 위해서 $q(x_{t-1}|x_t,x_0)$와 $p_{\theta}(x_{t-1}|x_t)$를 알아야 한다.

1. $q(x_{t-1}|x_t,x_0)$
   이는 아래와 같이 정의된다.
   

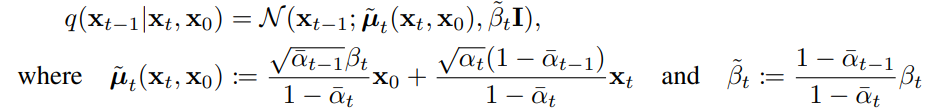
   Note: 증명은 diffusion model 를 참고할 것. 더 공부해야함.

2. $p_{\theta}(x_{t-1}|x_t)$
   이를 구하기 위해선, $\sum_{\theta}$ 와 $\mu_{\theta}$를 알아야한다.(Reverse process 식 참고)

• $\sum_{\theta}$
  $p$의 표준편차는 $\sigma^2_tI$라는 상수 행렬로 정의한다. 그러므로 이에 대해선 학습이 필요하지 않다.

• $\mu_{\theta}$
  $p$의 평균은 아래와 같이 정의한다.
  

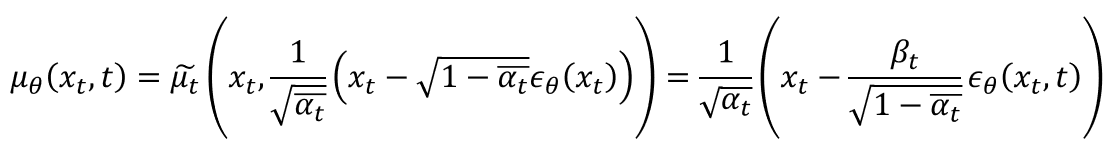
이제 우리는 $p_{\theta}(x_{t-1}|x_t)$로부터 $x_{t-1}$을 샘플링할 수 있다. 아래는 샘플링 과정에 대한 논문의 알고리즘이다.

또한 우리는 이렇게 얻어낸 파라미터들을 활용해 결과적으로 아래와 같이 KL divergence를 계산한 식으로 표현할 수 있다.

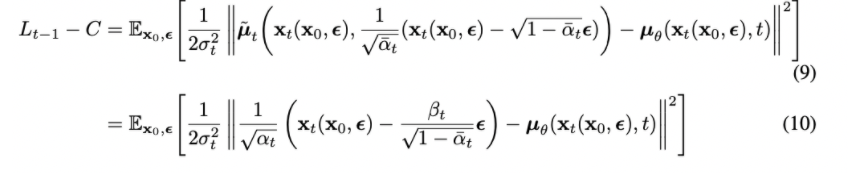
Note: 이렇게 되는 과정은 공부해봐야 함.

마지막으로, 우리는 위의 Loss function을 epsilon에 대한 식의 형태로 표현할 수 있다. 이를 Simplified Objective Function이라고 부른다.

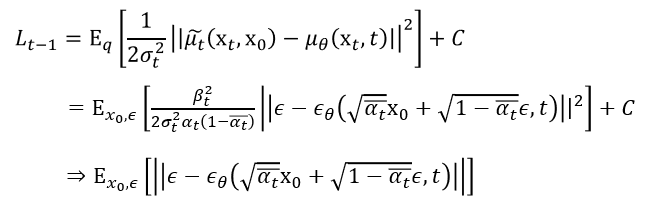
DDPM의 training 과정을 논문에선 아래 알고리즘으로 간단하게 제시한다.

$L_0$

Loss function의 마지막 구성 요소인 $L_0$는, 간단한 두 normal 분포 사이의 KL divergence 이다. 즉, 아래와 같이 표현할 수 있다.

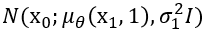
결론

• 결국 DDPM 논문은 reverse diffusion proecess의 $L_{t-1}$을 좀 더 학습이 잘 되도록 정리한 것이다.
• 이를 통해 더 좋은 퀄리티의 사진들을 만들어냄을 Experiments 절을 통해 보여준다.

Appendix

Loss의 수식전개 과정

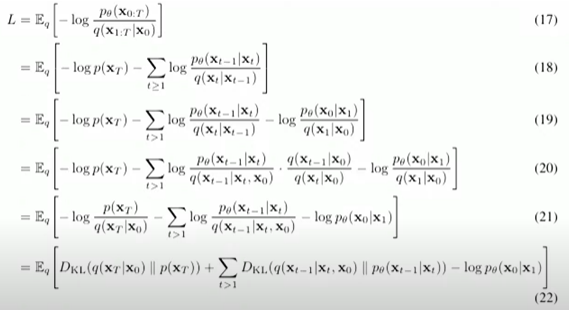
(18) -> (19)
t=1 인 case를 밖으로 꺼냄.

(19) -> (20)

• Markov Chain 성질에 의해, $q({x}_t|x_{t-1}) = q(x_t|x_{t-1}, x_{0})$ 로 확장 가능
• 이후 bayse rule 을 이용,

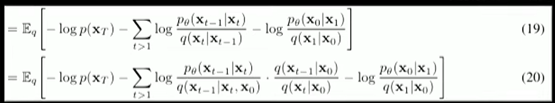
(using Markov Chain)

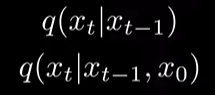
(using bayse rule)

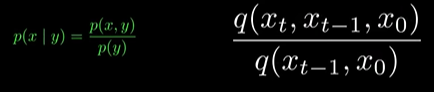
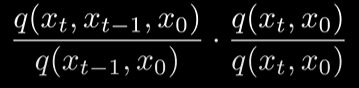
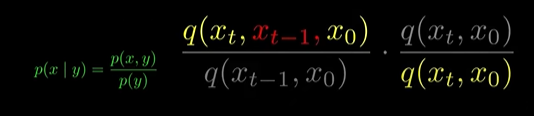
(다시 bayse rule)

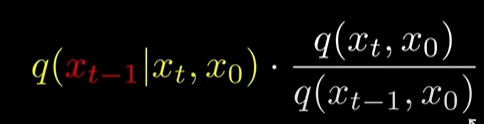
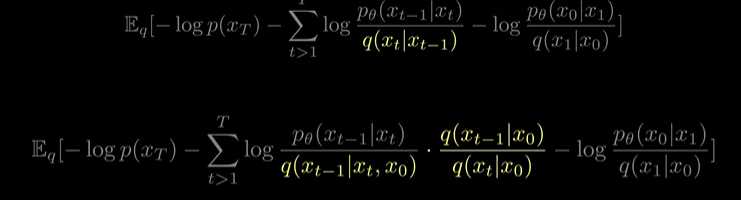
(20) -> (21)

• log의 성질 이용해서 sigma term 분리
  
  
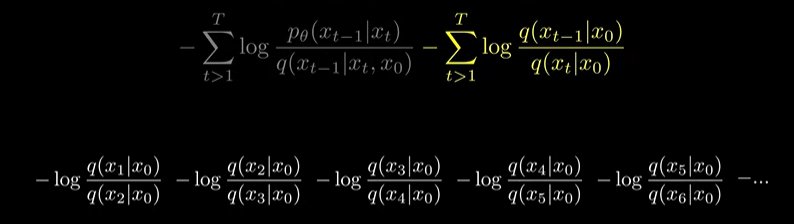
  (log의 성질 이용해서 분자, 분모 약분)
  
  (이 term과 아까 빼놓은 t=1 인 term끼리 약분 후, 남은 부분을 앞으로 빼냄)
  

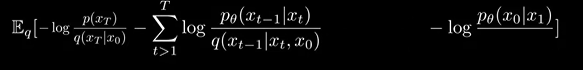
(21) -> (22)
남은 식의 앞의 두 term은 KL Divergence가 됨.

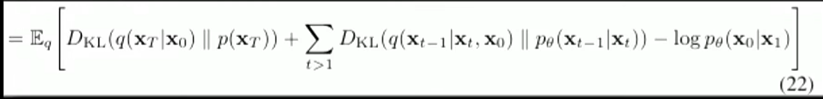
Background Math

Markov Property

현재 상태가 미래 상태에 대한 모든 정보를 제공한다는 것을 의미.
즉, 과거의 상태들은 미래 상태를 예측하는 데에 직접적인 영향을 끼치지 않음.

$P(X_{t+1}=x|X_t=x_t, X_{t-1}=x_{t-1},...,X_0=x_0) = P(X_{t+1}=x|X_t=x_t)$

• $X_t$: 시간 $t$에서의 상태.
• $P(X_{t+1} = x \mid X_t = x_t)$: 현재 상태 $X_t$가 주어졌을 때 다음 상태 $X_{t+1}$이 $x$일 확률.

현재 상태 $X_t$ 만이 다음 상태 $X_{t+1}$을 결정. 이전 상태 ($X_{t-1}, X_{t-2}, ...$)는 영향을 미치지 않음.

Markov Chain

Markov Property를 만족하는 상태들의 연속된 열.
각 상태는 전이확률에 따라 다음 상태로 전이됨.

• 상태 공간: $S={s_1, s_2, ..., s_n}$
• 전이 행렬: $P = [p_{ij}]$, 여기서 $p_{ij} = P(X_{t+1} = s_j \mid X_t = s_i)$

전이 행렬 $P$의 각 원소 $p_{ij}$는 상태 $s_i$에서 상태 $s_j$로 전이될 확률을 나타냄.

KL divergence

해당 논문에선 KL divergence에 대한 지식이 필수적으로 요구된다.
아래 두가지 블로그를 참고하자.
시각화
이론