포아송 분포와 비트코인 해킹 가능성

Index

1. 포아송 분포

2. 비트코인과 블록체인, 그리고 51% 공격

3. 비트코인에서의 포아송 분포

---

1. 포아송 분포

1) 이산형 확률 변수(Discrete Random Variable)

통계학에는 크게 확률 변수의 값이 이산적인지, 연속적인지의 여부에 따라 이산형 확률 변수(Discrete Random Variable), 연속형 확률 변수(Continuous Random Variable)로 구분한다.

다시 말해서, 특정 random variable의 벡터 $\vec x = (x_{1},...,x_{n})\in \R^{n}$가 있다고 하자. 이 때, $x_{i}$의 데이터 타입이 1개, 2개, ... N개 등 우리가 "셀 수 있는" 불연속적인 단위로 표시된다면 이산형 확률 변수에 해당한다. 반면, $x_{i}$가 가격이나 날씨, 속도 등 float 타입을 갖는 데이터의 경우에는 연속형 확률 변수에 해당한다.

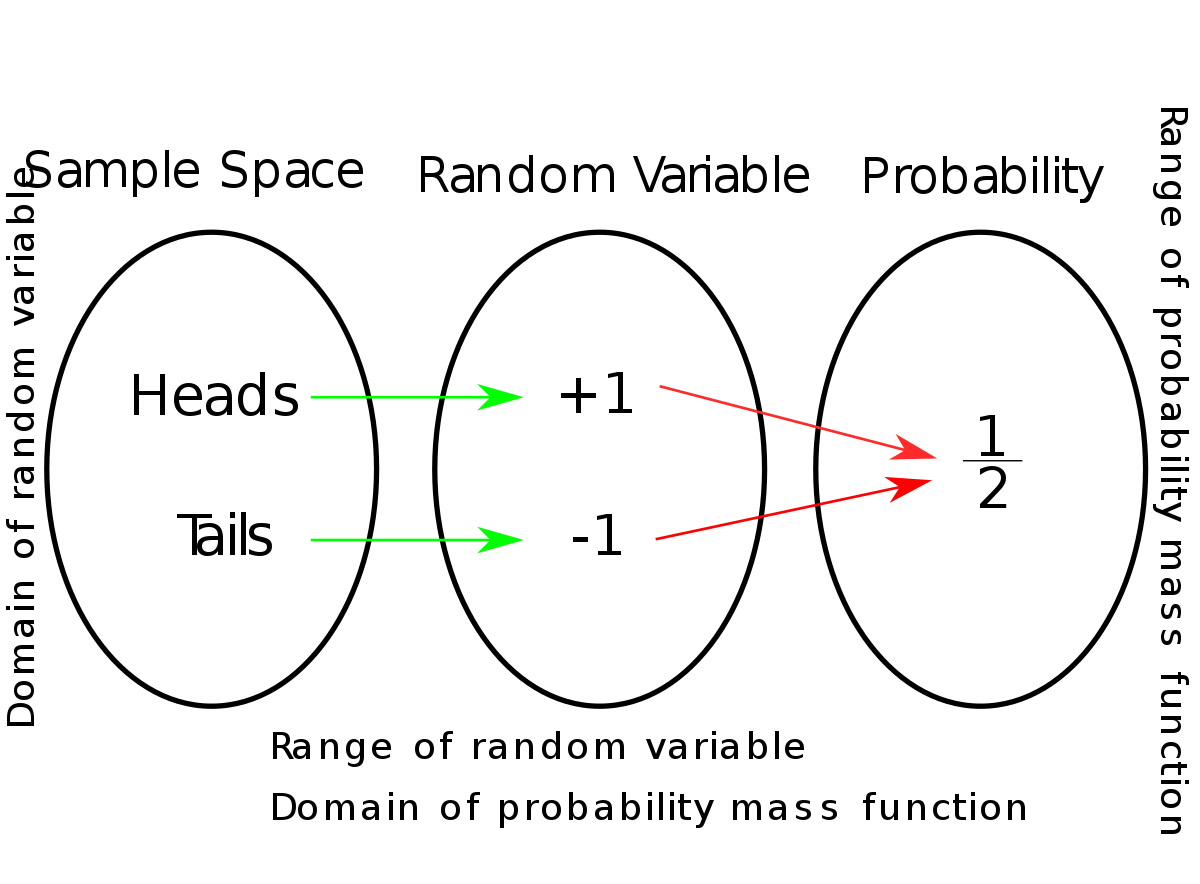
가장 구분되는 특징은 확률분포함수($f(x)$)의 개형인데, 연속형 확률 변수의 경우 정의역으로서의 확률 변수가 구간으로 나누어지지 않고 연속적으로 그려지는 모습을 볼 수 있다. (각 변수별 확률분포함수는 아래 그림을 참고)

Probability Distribution of Random Variables

2) 포아송 분포의 정의와 특징

포아송 분포를 따르는 확률 변수 $X$가 있다고 할 때, 이 $X$는 "발생가능성이 희박한 사건"에 대하여 단위시간 또는 단위공간 내에서 이 사건이 발생하는 횟수를 의미한다.

$X$를 포아송 확률 변수, $\lambda$를 포아송 확률 분포의 모수(기댓값, 분산), $f(x)$를 $X$의 확률질량함수(PMF)라고 할 때 아래와 같이 정리할 수 있다.

확률질량함수의 정의

$X\sim Poi(\lambda)$,

$f(x) = P(X=x) = {e^{-\lambda}\lambda^{x}\over x!}, \,\,x=[0,\infin]$

모수(Parameter) : 사건의 평균 발생 횟수

• $E(X) = \lambda$
• $Var(X) = \lambda$

기댓값과 분산이 같은 것이 포아송 확률 변수의 큰 특징으로, 자세한 증명은 수리통계학을 참고하세요 :)

포아송 확률 과정의 가정 및 특징

기본 가정

단위 시간 당 0 또는 극소수의 사건만 발생하며, 해당 시간 범위 내에서 서로 다른 시각에서의 사건 발생은 서로 독립 사건.

주요 특징

• 시간은 연속적이나, 시행 결과로써의 확률 변수값은 이산적인 확률 과정임
• 각 사건이 발생하는 시간 간격은 상호 독립적임. 즉, 발생 시간은 일정한 규칙성을 갖지 않음
• 단위 시간 당 사건의 평균 발생수는 $\lambda$ ($=E(X)$)
• 단위 시간을 매우 작은 시간 간격인 $\Delta$ 로 나누면, $\lambda/\Delta$개 만큼의 사건이 구간마다 평균적으로 발생함

참고로, 포아송 분포는 몇가지 조건을 충족할 경우 이항 분포(Binomial Distribution)에 근사하는 특징을 갖고 있는데, 해당 관계성 수리통계학 내용을 통해 살펴보시길 바랍니다 :)

---

2. 비트코인과 블록체인, 그리고 51% 공격

블록체인은 $i$번째 블록 $B_{i}$이 $i$$-1$번째 블록의 Block Hash, 즉 previousHash를 참조하며 이어지는 Linked List 형태의 거대한 자료구조이자 분산 DB 정도로 이해할 수 있다.

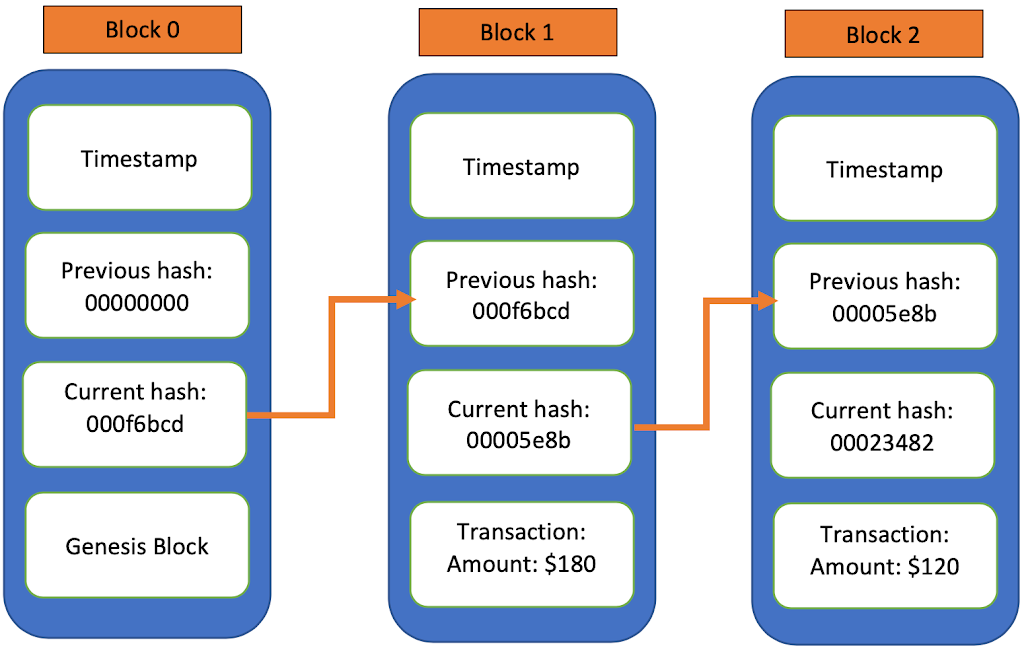
Blockchain in Python (Block Structure)

class Block(object):
    def __init__ (self, index, transaction, previousHash, difficulty): 
        self.index = index
        self.transaction = transaction
        self.previousHash = previousHash
        self.difficulty = difficulty
        self.timestamp = datetime.now()
        self.nonce = 0
        self.hash = self.mineBlock()

"A Block object is initialised with an index, which corresponds to the index on the Blockchain instance on which it resides. It also required a record of transaction(s), the hash from the previous block, proof of work difficulty, a timestamp at time of creation and an initial nonce value. This data is all fed into a hashing algorithm, which recalculates in a loop with a new nonce value each time, until a suitable block hash is found that meets the predefined difficulty level.

• quoted from sheldonbarry.com

51% 공격

우선, 비트코인 논문(https://bitcoin.org/bitcoin.pdf)에서는 51% Attack이라는 워딩 자체는 어디에도 없다. 그러나, 다수의 공격자(Attacker)를 경계하는 내용은 논문 내용 가운데 총 24곳에 분포되어 있다.

전부 다 살펴볼 수는 없고, 51% 공격과 관련하여 저자가 우려하는 결론을 나의 문장과 논문의 한 문장으로 정리하자면 다음과 같다.

과반에 해당하는 공격자 노드(Attacker)가 블록체인 네트워크의 Hash Power를 장악하여 현재 유효한 체인의 Path를 바꾸고, 이에 따라 현재 시점 이전의 블록의 내용을 변경하는 것을 막아야 한다. 이 때의 목적은 블록체인의 데이터 무결성을 확보하는 것이다.

"...the verification is reliable as long as honest nodes control the network, but is more vulnerable if the network is overpowered by an attacker..." (Quoted from the paper)

우리가 이번 포스팅을 통해 살펴보고자 하는 것은 비트코인 블록체인 네트워크에서 공격자가 공격에 최종 성공할 사건이 단위 시간 내에 매우 적게 발생할 것이라는 것이고, 이 공격이 성공할 확률 역시 체인의 길이가 길어질수록 0에 수렴한다는 것을 증명하는 것이다.

---

3. 비트코인에서의 포아송 분포

Honest Node vs Attacker : Random Walk Process

논문에서 이야기하고 있는 것처럼, 정직한 노드와 공격자 노드가 싸움을 하는 게임은 이항 랜덤 워크(Binomial Random Walk) 과정으로 볼 수 있다. 이때, 정직한 노드에 의해 블록이 1개 추가되는 것을 성공 사건, 공격자 노드에 의해 블록이 1개 추가되는 것을 실패 사건이라고 정의해보자. 그리고 성공 1개가 발생할 때마다 게임의 점수는 1씩 증가하고, 반대의 경우 1씩 감소한다.

이러한 게임에서 성공과 실패의 확률(또는 비중)을 각각 $p$, $q$라고 정의하고, 현재 블록의 길이로부터 $z$번째 앞의 블록에서 공격자 노드가 정직한 노드를 따라잡을 확률을 $q_{z}$로 정의해보자. 이를 따라 수식을 만들면 아래와 같다.

이 때, 공격 노드가 블록을 생성하는 비중이 정직한 노드보다 많거나 같으면 네트워크 점유율이 과반을 차지하고 공격에 성공하는 상황이라고 보며, 이 때의 $q_z$는 당연히 1이 된다. 그 반대의 경우에는 개별 사건이 $z$번 독립 시행으로 발생하므로 $q_z$는 $(q/p)^z$가 된다.

공격자 노드가 블록체인 네트워크를 공격할 사건이 포아송 분포를 따른다고 한다면, 해당 사건의 기댓값($E(X)$=$\lambda$)는 아래와 같이 작성해볼 수 있다.

위 기댓값이 정의되는 구조를 말로 풀어보면 이렇다.

정직한 노드가 블록을 생성하는 비중에 비해 공격자 노드가 블록을 생성하는 비중
(단, 관측 시점 현재 $i$번째 블록을 $B_{i}$라 했을 때, $B_{i-(z-1)}$ 블록까지가 관측 구간; 총 $z$개의 블록을 관측)

위 값을 모수로 갖는 포아송 확률변수 $X$가 있다고 할 때, 해당 변수의 pmf는 아래와 같다.

• $f(x) = P(X=x) = {e^{-\lambda}\lambda^{x}\over x!} = {e^{z(q/p)}\,(z(q/p))^{x}\over x!}$

그리고 PMF의 정의에 의해 아래와 같은 수식이 성립한다.

• $\sum_{x=0}^{\infin}f(x) = \sum_{x=0}^{\infin}{e^{z(q/p)}\,(z(q/p))^{x}\over x!}= 1$

공격 가능성에 대한 증명

1) 변화하는 z에 따른 공격 성공 가능성

$q$, 즉 공격자가 다음 블록을 찾아낼 확률을 각각 $0.1$, $0.3$으로 고정시켜두었을 때, $z$의 값은 어느 정도가 되어야 최종적으로 공격에 성공할 가능성이 희박해지는지 모델링한 결과이다.

z축에 따라 PMF를 그려보면 포아송 확률 분포의 확률값은 급격하게 우하향하는 개형이 된다.

2) 공격 성공 가능성이 0.1% 미만일때의 (q,z)

이제는 포아송 확률 변수의 확률값 자체를, 즉 공격자가 공격에 성공할 가능성을 사전에 $0.1$% 미만으로 제한해둔다면 공격자가 블록을 찾아낼 확률 $q$와 이에 따른 $z$는 어느 정도가 되는지 모델링한 결과이다.

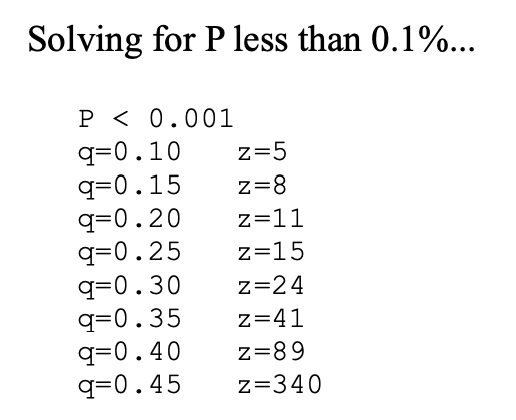
결과를 찬찬히 해석해보면, $z$가 커질수록, 즉 현재 시점으로부터 더 많은 블록이 쌓여있을수록($\because$ 전체 관측 구간이 커지는 것이므로) 악의적인 노드가 만들어내는 블록의 비중도 커지는 것을 볼 수 있다.

현재 블록의 인덱스보다 340이 작은 블록, 그러니까 340번째 앞에 있는 블록부터 공격이 발생한다고 한다면 그 지점부터 공격자와 정직한 노드의 비중은 45:55로 거의 반반에 해당할만큼 공격자의 채굴 비중 자체는 큰 편인 것으로 보인다.

---

Reference

• 비트코인과 수학공식
• Bitcoin 논문