경사하강법이란? (네이버 ai 부캠 9일차. )

이호용·2021년 1월 31일

네이버 ai 부스트캠프

목록 보기

12/12

경사하강법(순한맛)

미분의 개념과 그래디언트 벡터에 대해 설명합니다.

경사하강법의 알고리즘과 실제 코드에서의 구현을 보여줍니다.

접선의 기울기를 이용해서 함수의 최솟값으로 점을 이동시키는 원리를 알면 이를 바탕으로 경사하강법의 알고리즘과 수식을 이해할 수 있습니다.

특히 변수가 벡터인 경우, 편미분을 통해서 구한 그래디언트 벡터를 통해 d-차원으로 경사하강법을 확장할 수 있다는 개념을 확실하게 잡고 가시기 바랍니다.

미분이 뭔가요?

미분은 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구, 최적화에서 제일 많이 사용하는 기법
sympy.abc라는 모듈에 diff라는 함수를 이용하면 미분을 사용할 수 잇다.

파이썬에선 아래 코드를 입력하면, 미분을 해볼수 잇다.

import sympy as sys
from sympy.abc import x
sys.diff(sys.poly(x**2+ 2*x+3),x)

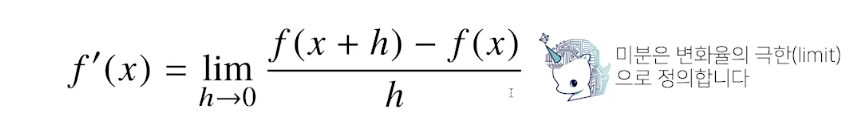
미분을 이해해보자.

미분은 함수 f의 주어 진 점 (x,f(x))에서의 접선의 기울기를 구한다.
한점에서 접선의 기울기를 구하면 점의 위치가 어느 방향으로 움직여야 함수값이 증가하는지, 감소하는지 알 수 있다.(함수를 증가시킨다?)
이차원의 함수가 있다고 가정했을떄, lim h->0의 순간 x값의 아주 작은 변화의 차에대한 비율을 구하면, 이차원 함수의 x값에 대한 기울기를 구할수 있다. 이 기울기가 의미하는 바는, 그 순간 지점의 x이동량에 대한, y값의 변화율을 의미한다.
함수의 결과 값을 증가시키고 싶으면, 미분값을 더하고, 함수를 감소 시키고 싶으면 미분값을 뺸다
미분값을 더하면 경상상승법(gradient ascent)이라 하며, 함수의 극대값의 위치를 구할 떄 사용한다.
미분값을 뺴면 경사하강법 이라 하며, 함수의 극소값 의 위치를 구할떄 사용한다.
고로 미분한 값을 알면,
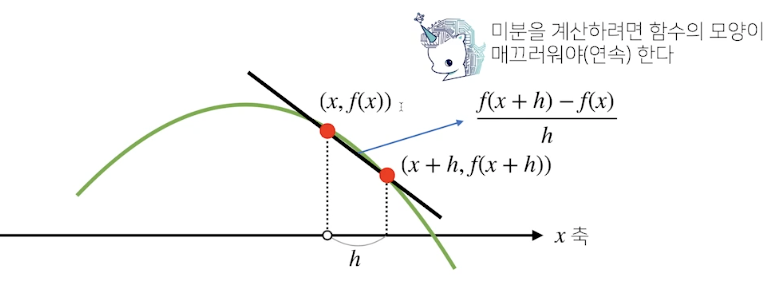
h를 0으로 계속해서 보내주면
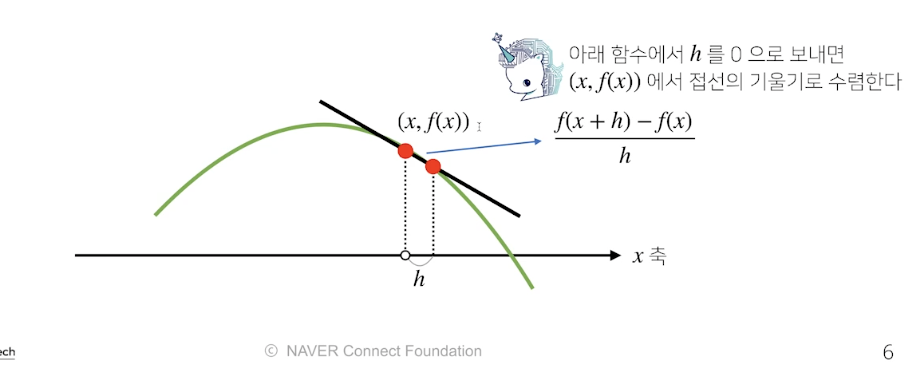
h의 크기가 계속 작아지다 보면 결국 한점에서 기울기를 구할수 잇다.

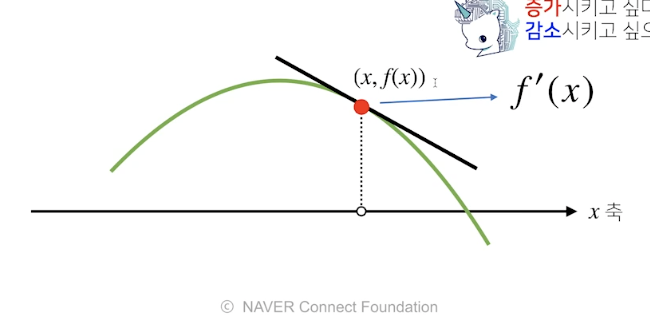
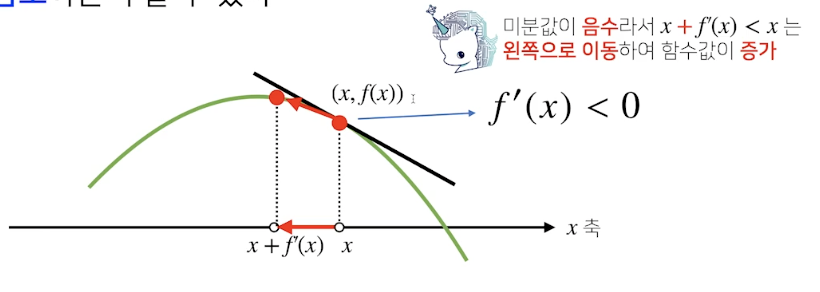
미분을한 f'(x) 값이 f'(x)<0 위와 같은 그림이면, f'(x)를 x를에 더해 주면, x축이 왼쪽으로 이동하고
f'(x) + x 에서 의 기울기의 절대값은 점점 작아진다. 결국엔 기울기가 0 에 가까워지고
주어진 함수의 미분값이 0이 될때 까지 반복한다면, 함수에서 나올수 있는 최대값의 위치에서 멈추게 된다. 이를 경사상승법 이라고 한다.

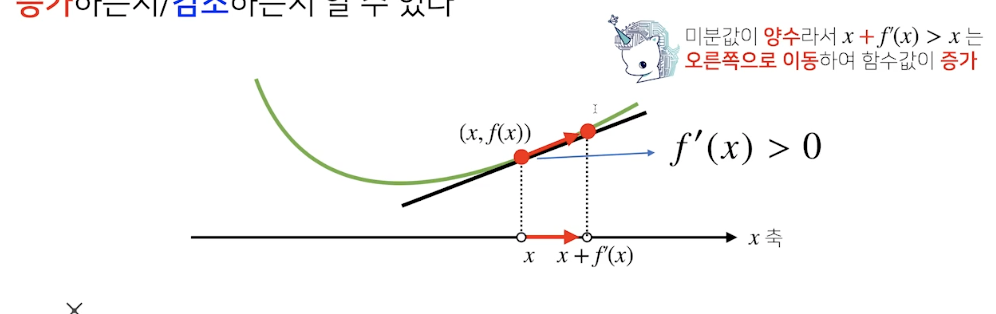
반대로 미분값이, f'(x) > 0 일떄 f'(x) + x를 해주면, 미분이 오른쪽으로 이동한다.

위의 두 상황 모두 미분값을 더하게되면, 미분 값이 최대일떄의 값을 구할수 있게 된다.

var = list 
grad = gradient(var)
while(abs(grad) > eps):
	var = var -lr *grad
    grad = gradient(var)

변수가 벡터이면요?

위의 상황에서는 x가 + 이냐 -이냐 일떄만 고려를 했지만, 만약 변수가 벡터라면?
3차원이라고 가정하면, 두 방향이 아니라 세 방향을 가지게 된다 .이런 경우에는 편미분(특정 방향의 좌표로 미분하는것)을 취해준다.
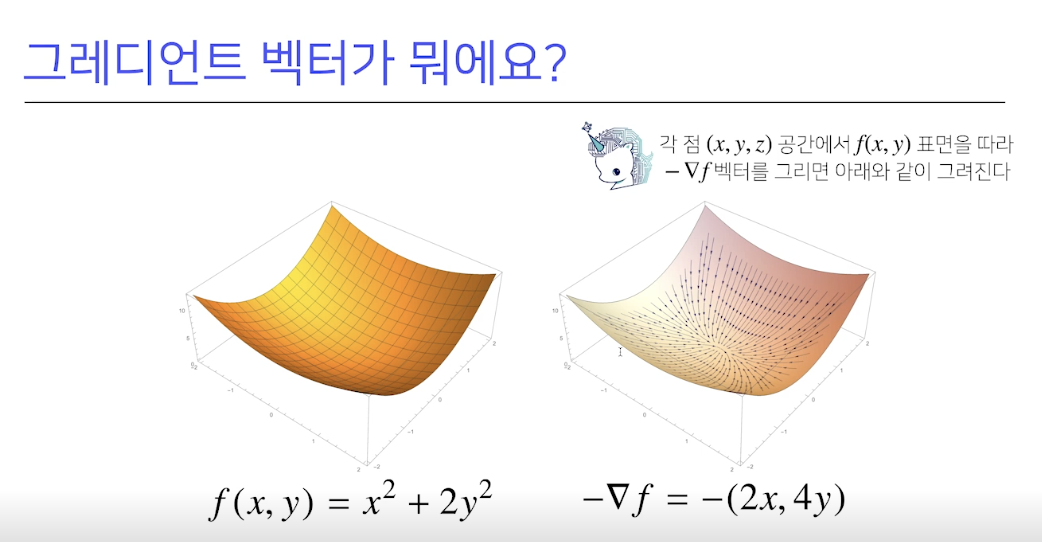
이렇게 d차원 벡터를 입력으로 한 변수를 사용한다면,각 미지수 d개를 편미분 해서 계산해야하는데, 이렇게 각 미지수별로 편미분해서 나열할수 있는데 이 벡터를 그레디언트 벡터라고 한다.
∇ : 나블라 라고 한다. {\displaystyle \nabla }\nabla
∇f 라고 표기하면, f라는 함수의 미지수 들에대한 편 미분 을 한 값들을 나열한 벡터를 의미한다.
이렇게 구한 그레디언트 벡터는 2차원에서 미분의 했던 값처럼, 함수에서 뺴주면 경사하강법이 적용되고 더해주면 경사상승법이 적용된다.

코드로 적용

var = init
grad = gradient (var)
while(norm(grad) > eps):
	var = var - lr * grad
    grad = gradient(var)

앞의 2차원의 하강법과 다른점은, 미분한 grad의 값은 벡터로 이루어 져 있기떄문에, 노름의 크기로 계산을 한다는 점이다.

경사 하강법(매운맛)

gradient: 미분을 계산하는 함수

init: 시작점,lr: 학습률,eps: 알고리즘 종료조건

var = init
grad = gradient(var)
while(abs(grad) > eps):
 var = var - lr * grad
 grad = gradient(var)

n개의 데이터로 이루어진 상황에서 데이터를 가장 잘 차즌ㄴ 방법을 선형 회귀분석을 설명햇다. 지난 시간에는 무어펠런즈의 역행렬에 의해 해를 찾는것에 대해 설명을 했다.

이번 시간에 무어펠런즈 역행렬을 사용하지 않고 경사하강법으로 선형모델을 찾는 방법을 배워 보겟다.

선형 모델을 이용해서 분석을 한다면 무어펠러즈 역행렬만 이용해서 분석을 해도 되지만, 선형모델이 아닌 다른 모델도 이 경사하강법을 통해 찾을 수 있기 떄문에 이 방법을 알아본다.

무어펠로즈의 역행력을 이용해서 선형 회귀를 찾는 방법도, 좋지만 경사하강법을 이용하면, 선형 회귀말고 다른 모양(다차원)의 회귀들도 분석 할수 있기 떄문에, 경사하강법을 배운다.
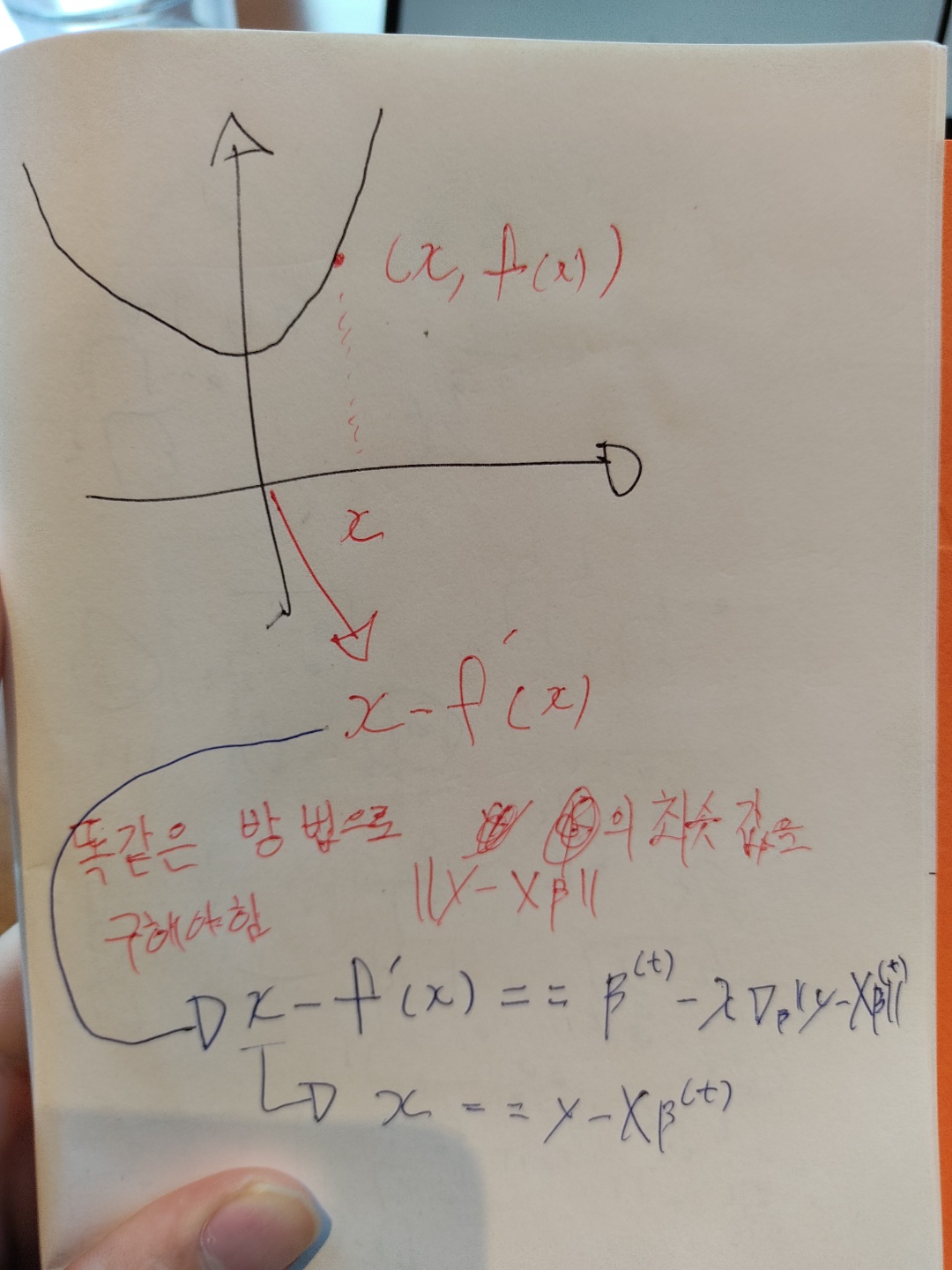
우리가 해야할것, 위의 사진에서 y-XB^(t) 라는 값을 최소화 될때까지 경사하강법을 진행해가며, 최솟값을 구해주어야함!!!
함수의 값을 최소화하거나, 최대화하거나 하는 목적을 가진 함수를 목적 함수(Objective function)라고 합니다.

목적식 == ||y - X*(벡타)||2 노름의 최솟값을 구하는 건 똑같다.
이렇게 구한 선형회귀 목적식을 벡타에 대해 미분을 한 다음에, 주어진 벡타에서 미분한 값을 뺴게 되면 경사하강법에서 최소화 되는 값을 구할수 있따.

||y-XB||2 -> ||y-XB||2^2

기존 목적식에서 제곱의 최솟값 구하기.
제곱의 최솟값의 경우, 구하는 방법은 같지만, 이렇게 하면, 식이 간단해 진다.
y-XB 의 값이 증폭이 될테니, 더 정확해진다.

코드

for t int range(T):
	error = y - X @ beta
    grad = -transpose(X) @ error
    beta = beta - lr * grad

경사하강법은 만능일까?

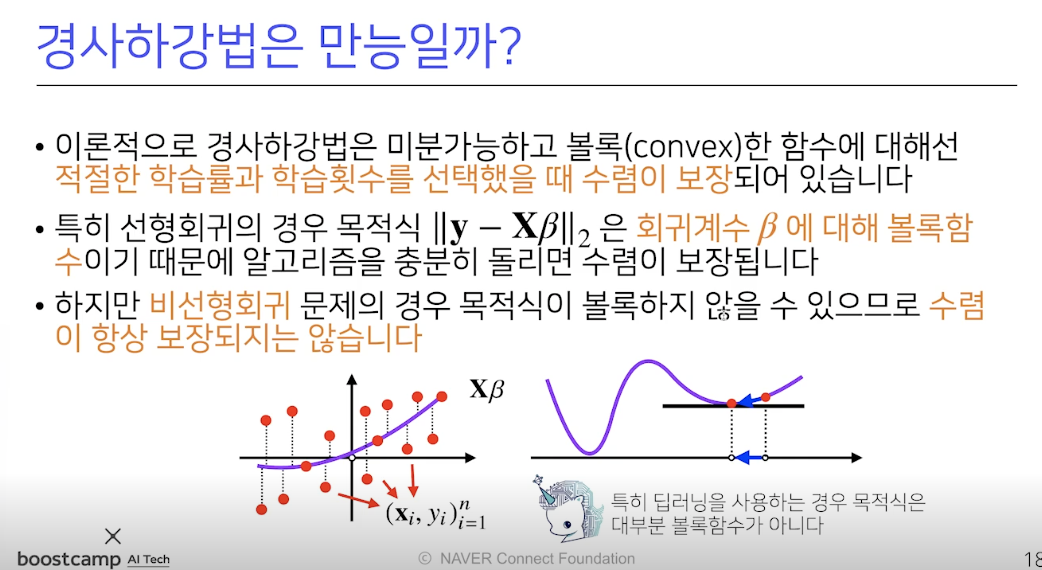
위의 상황처럼 볼록한 모양은 꼭 하나가 아닐수 있다, 원하는 최저 점을 못 찾을수도 있기 떄문에, 우리가 원하는 y-X^b의 최솟값을 나오게 하는 b를 찾을려면 확률적 하강법을 통해 b의 값을 찾아야한다.

확률적 경사하강법

앞서 구했던 경사하강법의 경우 모든 데이터를 이용해서, 계산하는게 아니라, 한개 또는 일부의 데이터를 이용해 구함.
SGD 라고함. 경사하강법 보다, 연산 자원을 효율적으로 관리 가능.

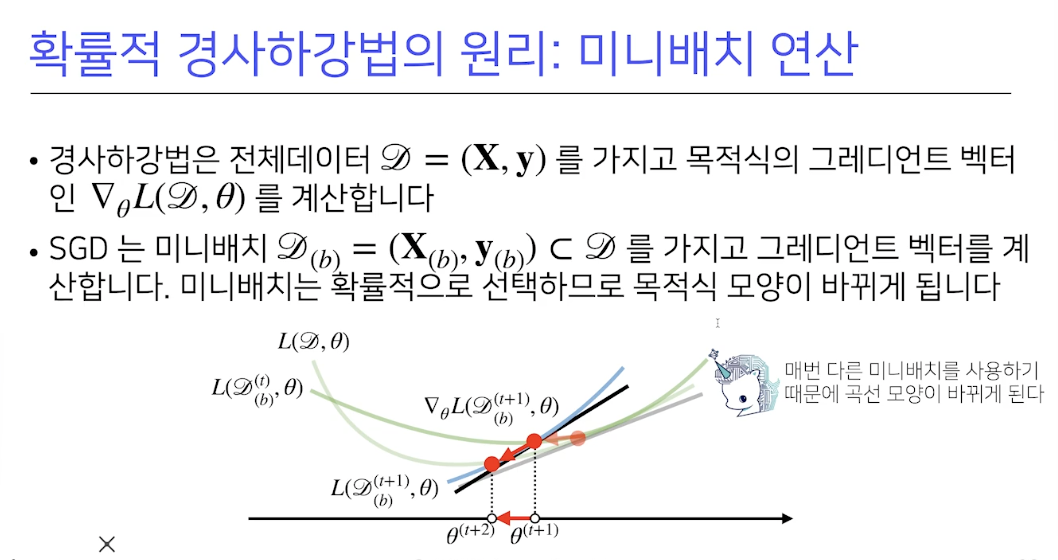
계산을 할떄마다, 목적식이 바뀌기 떄문에, 처음 사진에서 처럼, 극소점이 아닌 경우에 멈출일이 없어진다!!

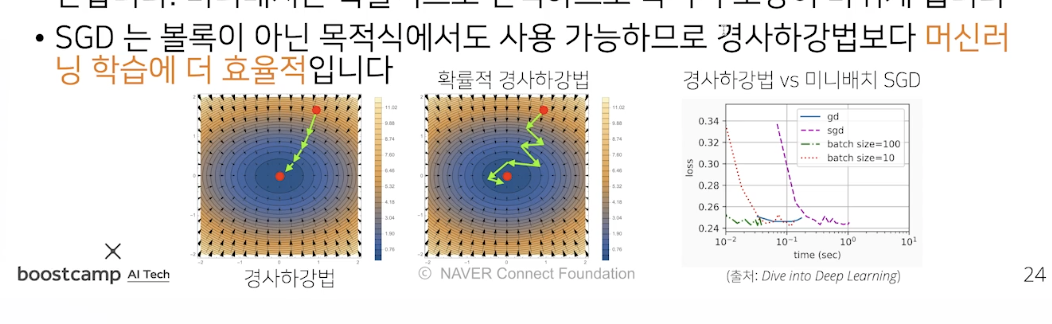
경사 하강법이 가능방향이 최적화 되진 안았지만, 확률적을 쓰게 되면, 모든 데이터를 가지고 계산하는게 아니라, 속도 측면에서는 sgd가 더 빠르다.

이호용

~_~

이전 포스트