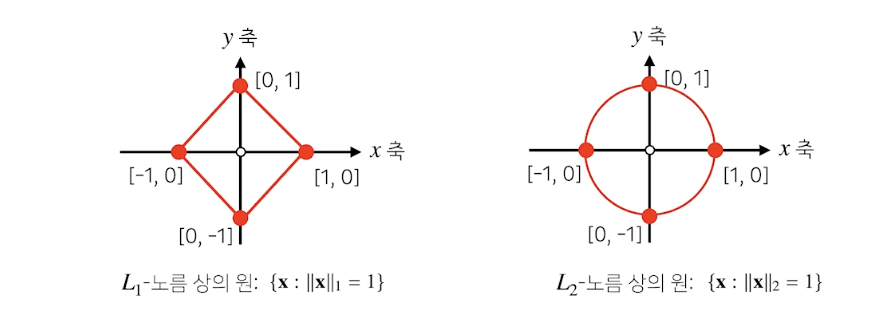이 페이지는 유니스트의 임성빈교수님의 강의 자료를 참고 하였습니다.

벡터가 뭐에요?

벡터는, 딥러닝에서 매우 중요한 선형대수학의 기본 단위가 되고, 벡터간의 연산을 단순히 숫자 계산으로 끝내기보단, 공간에서 어떤 의미를 가지는지를 이해하는 것이 중요합니다.

• 벡터는 숫자를 원소로 가지는 리스트 또는 배열이다.
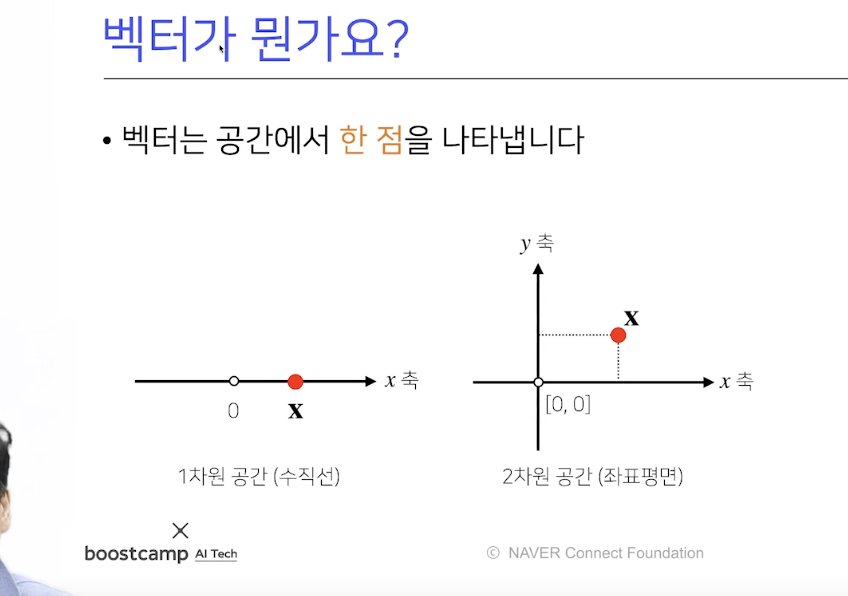
• 백터는 공간에서 한점을 나타냅니다.
• 백터는 원점에서부터 상대적 위치를 표현합니다.
• 백터에 숫자를 곱해주면 길이만 변하는데, 여기서 곱해주는 값을 스칼라 곱이라고 합니다.
• 벡터끼리 같은 모양을 가지면(행렬이 같으면) 덧셈, 뺠셈을 계산할수 있습니다.
• 벡터끼리 모양이 같으면, 성분곱(hadamard product)이 가능하다.
• 두 벡터의 덧셈은 다른 벡터로부터 상대적 위치이동을 표현합니다.

벡터의 노름 구해보기.

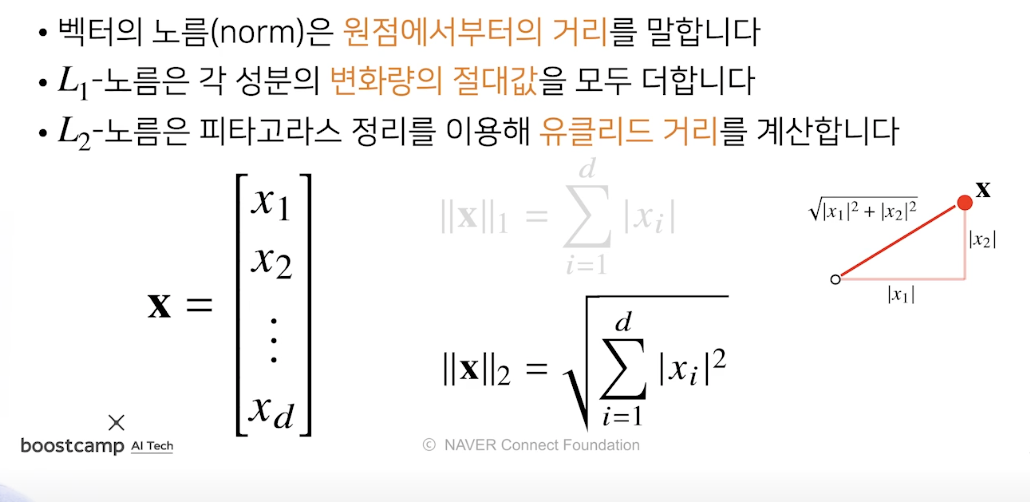
• 벡터의 노름은 원점에서부터 백터까지의 거리.
• L1은 각 성분의 변화량의 절대값을 모두 더합니다:(멘하튼노름)
• L2 노름은 피타고라스 정리를 이용해 유클리드 거리를 계산합니다. : (유클리드 노름)
• L1 노름 == ||x||1 은 |X1| + |X2| 로 더해서 구할수 있다.
• L2 노름 == ||x||2 은 sqrt(|x1|^2 + |x2|^2) 로 구할수 있다.
  

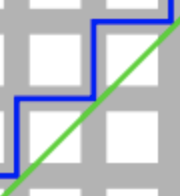
지도에서 갈수 있고 없고를 따지지 않고 최단거리를 구할떈 유클리드 노름, 거리에서 갈수 있는 거리중 가장 짧은 거리를 구할려면 멘하튼노름을 사용한다고 한다. 파란색 멘하튼 초록색 유클리드

왜 다른 노름을 소개하나요?

• 노름의 종류에 따라 기하학적 성질이 달라집니니다
• l1의 경우 [1,0]에서 [0,1]로 바뀔떄 유지해야하는 값은, |x1|+|x2|만 같게 유지하면 되어 마름모 모양이 나오지만, l2의 경우 대각선의 길이는 항상 일정해야 함으로 원의 모양이 나온다.
• 두 노름은 목적에 따라 무엇을 사용할지가 달라진다
• 두 벡터 사이의 거리를 구할때 ||x-y|| = ||y-x||의 형태가 가능하다.
• 순서에 상관없이 빼고 절대값을 씌우면 값이 나온다
  

두 벡터사이의 각도 구해보기

• l2 노름일때, 두 벡터사이의 거리를 구하면,

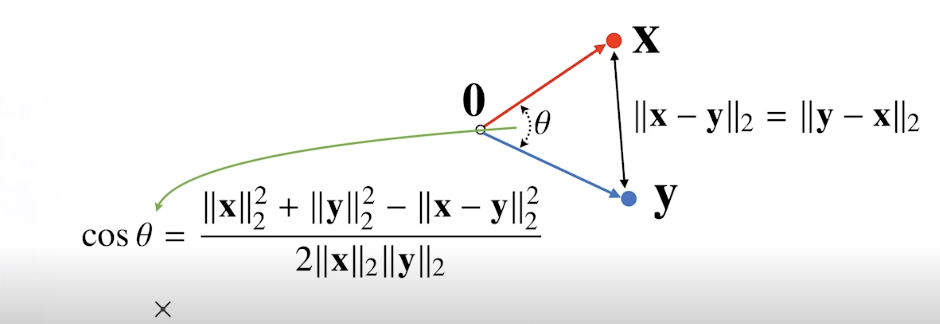
• 제2 코사인 법칙을 이용해 두 벡터 사이의 각도를 계산핤수 있다.
  
  

• 첫번째 사진의 분자가

• 0xy 라는 삼각형이 있을떄,각변이 x,y,0라면, cos(셉타) = |x|l2^2 + |y|l2^2 - |x-y||l2^2

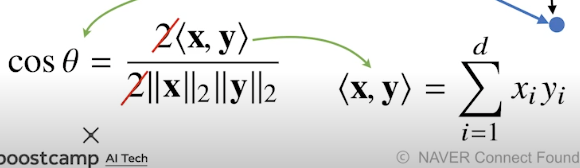
• 인데, 내적을 사용하여 2번쨰 사진처럼 간략하게 표현할수 있다.

• 코사인 (셉타)를 구하는 방법은 두벡터의 내적/|x|l2*|y|l2 하면 구할수 잇고,

• 이렇게 구한 값을 arccos(cos(셉타)) 를 넣어주면, 각도(라디안이 나온다)

  내적이란? 두벡터들의 성분곱들을 취하고 성분곱을 취한 모든 값들을 더해주는게 내적이다.

내적은 어떻게 해석할까?

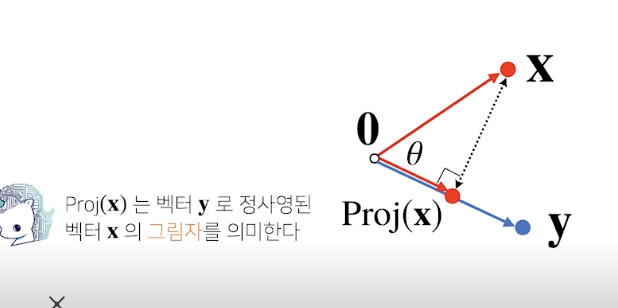
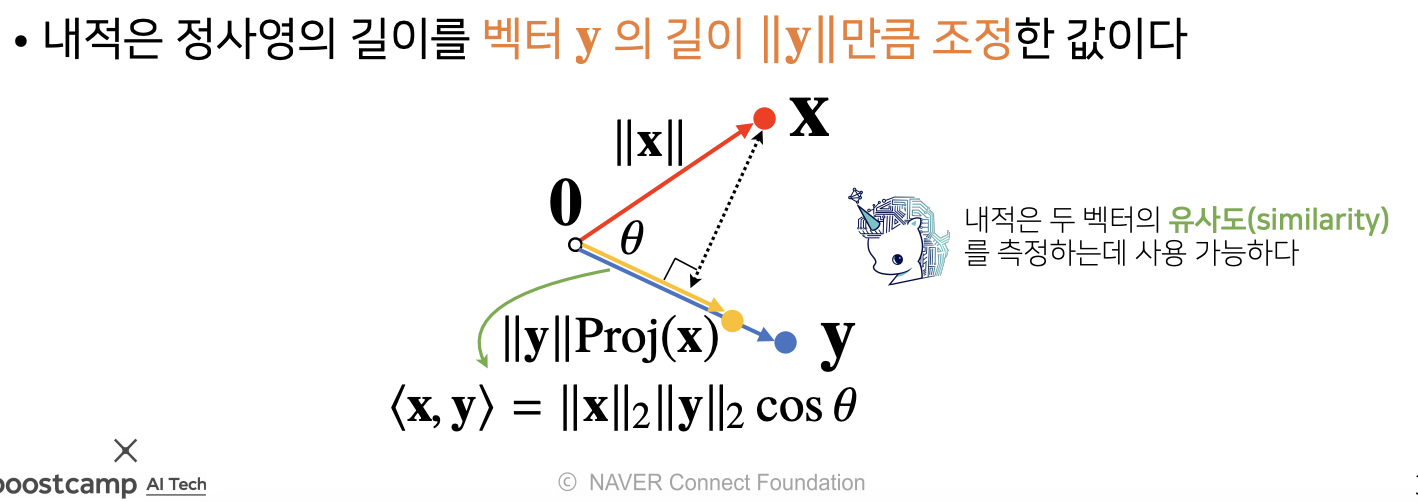
• 내적은 정사영(orthogonal projection)된 벡터의 길이와관련 있다.
• 정사영은 x라는 벡터와 y라는 벡터가 있을댸, x라는 벡터를 수직으로 내렸을때, y와 겹쳐지는 길이를 의미한다. 이 값의 길이가, 사진에서 처럼, ||x||cos(셉타)이며, 이렇게 구한 값이proj(x)이고
• 이렇게 구한 정사영에, y벡터를 곱해, ||y||만큼 길이를 조정한것이다.
  

행렬이 뭐에요?

벡터의 확장된 개념인 행렬은 행(row)벡터를 원소로 가지는 2차원 배열로 벡터와 다르게 계산되는 연산들에 주의하셔야 합니다.

행렬연산은 딥러닝에서 가장 핵심적인 연산이라고 볼 수 있을만큼 중요하고, 자주 사용되기 때문에 행렬 연산의 메커니즘,그리고 이 때 가지는 기하학적 의미와 머신러닝에서 어떻게 사용되는지를 충분히 이해하고 넘어가시기 바랍니다.

• 벡터는 숫자를 원소로 가지는 1 차원 배열이고, 벡터를 원소로 가지며, 2차원 인 리스트를 행렬이라고 한다.
• 행렬은 행(row)과 열 (column)이라는 인덱스를 가집니다.
• 먼저 행을 쓰고 뒤에 열을 쓴다.이름 그대로 라고 생각하자.

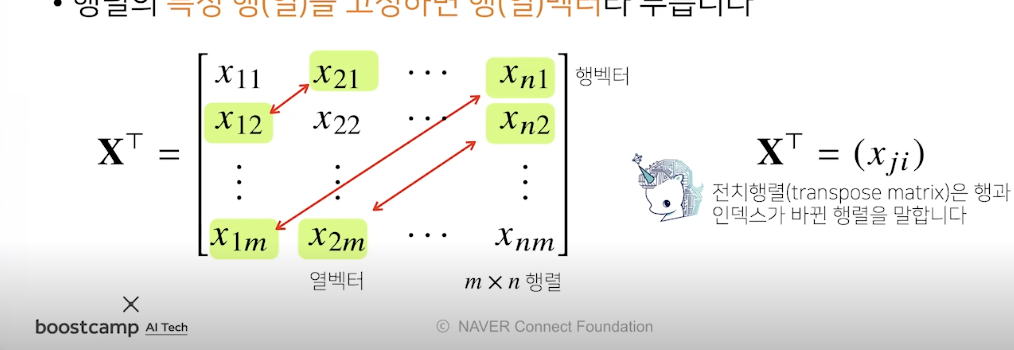
전치행렬(transpose matrix)

• Xij라는 행렬을 행과 열을 바꿔 Xji라고 하게 되면 이를 전치 행렬이라고 한다.
• 전치행령은 행렬 위에 T라는 문자를 붙인다.
  

행렬을 이해하는 방법

• 벡터가 공간에서 한 점을 의미한다면, 행렬은 여러점들을 나타냅니다.
• 여기서는 쉽게 아래 사진의 행 하나가 벡터 하나라고 생각하자, 행마다 벡터의 위치를 담고 있고 여러개의 점을 ㅅ찍을수 있따.
  

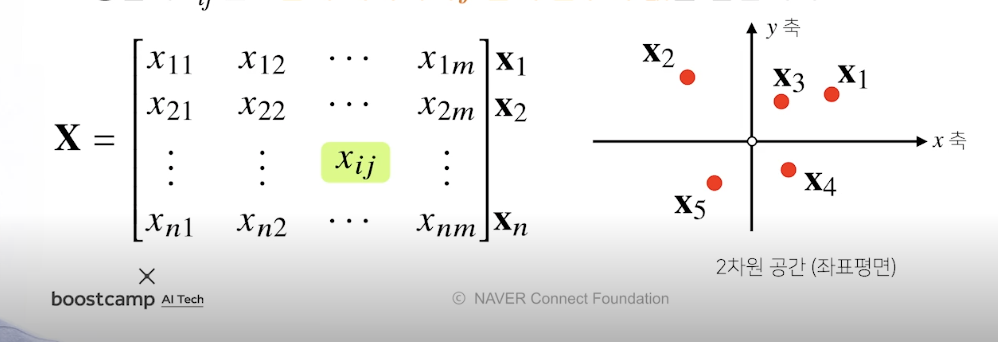
행렬의 덧셈 뻴셈 성분곱 스칼라곱

• 같은 모양의 벡터끼리 더하고 뻬기가 가능하듯 행렬도 마찬가지다.
• 행렬의 성분곱도 행렬의 더하기 뺴기를 하듯이. 벡터 각각의 성분들끼리 곱해준다.
• 행렬의 스칼라곱은 벡터의 스칼라곱이랑 일치한다. , 모든 행렬에 스칼라를 곱해주면 된다.
  

행렬 곱셈(matrix multiplication)

• 성분곱은 위치가 같은 요소 끼리 곱하는것이고 행렬곱은 행렬에서 사용하는 규칙으로 곱하겠다는 것을 의미.
• 행렬 곱셈은 i번쨰 행 벡터와 j번쨰 열 벡터 사이의 내적을 성분으로 가지는 행렬을 계산합니다.(그냥 행렬 곱할떄 했던거 처럼 곱하고 더한다는말.)
• 두행렬의 행벡터와 열벡터의 내적으로 구해진다는것을 알수 잇따.
• 고등학교떄 배웟던 행렬 곱과 같다.
• 앞의 행의 길이와 뒤에오는 행렬의 열의 길이가 일치하면 행렬의 곱이 가능하다.
  

행렬의 곱셈의 곱셈도 numpy에서 inner함수로 계산이 가능한데, inner는 X라는 행렬과 Y라는 행렬이 을 inner시키면, X*YT(뒤에 오는 행렬을 전치행렬로 만들어주어 곱한다.)

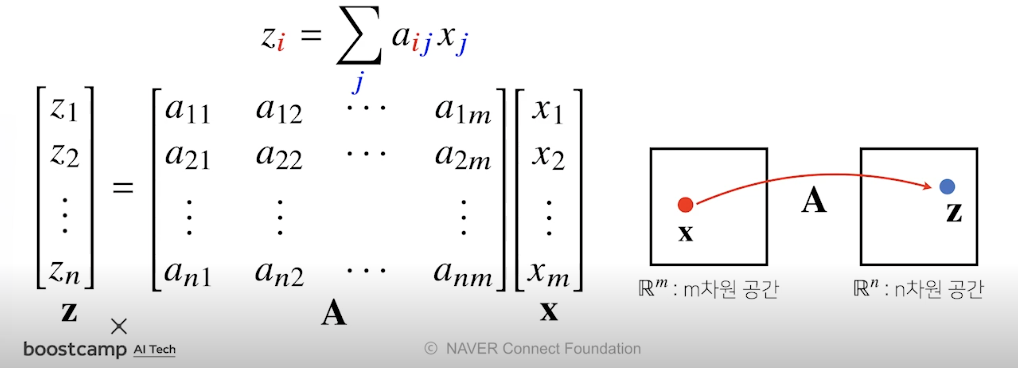
행렬을 이해하는 방법 (2)

• 행렬곱을 통해 벡터를 다른 차원의 공간으로 보내줄수 있다는 걸 의미합니다.
• 사진에서 보면, x라는 벡터를 z라는 벡터로 이동 시켜주는데 중간에서 중재해주는 역할을 한다고 해서 행렬은 연산자라고 도 불린다.
• 머신러닝에선 행렬의 연산자 기능을 통해서, 패턴 추출과, 데이터 압출을 할수도 잇습니다.
  

numpy에서 행렬의 곱

행렬의 곱은, @를 통해 나타낸다.

역행렬 이해하기.

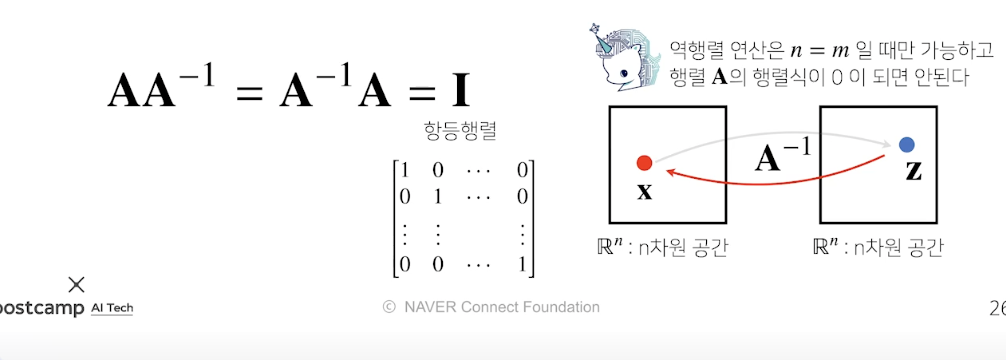
• 어떤 A의 연산을 거꾸로 되돌리는 행렬을 역행렬(inverse matrix)이 라 부르고 A^(-1) 라표기한다. 역행렬은 행렬 숫자가 같고 행렬식이 0이 아닌경우에만 사용할 수 있"다.
• numpy에서는 X라는 배열을 역행렬 할려면, np.linalg.inv(X) 이렇게 해버릴수 있다.
• 잘 만들어 졋는지 확인해볼려면, X@np.linalg.inv(X) == 항등행렬 인지 을 확인해보면된다.
  

유사행렬(무어펜로즈 역행렬)

• 기존에 배운 역행렬의 경우, 행과 열이 완전히 일치해야 사용할수 잇엇다.
• 하지만, 행과렬이 일치안해도 역행렬을 구할수 있는 방법이 있는데, 이를 유사역행렬 또는 무어펜로즈 역행렬 이라한다. A^+라고 표현한다.
• 유사 역행렬은, 행이 많은떄와 열이 많을떄에 따라서 다른 방법으로 역행열을 구한다.
  

사용
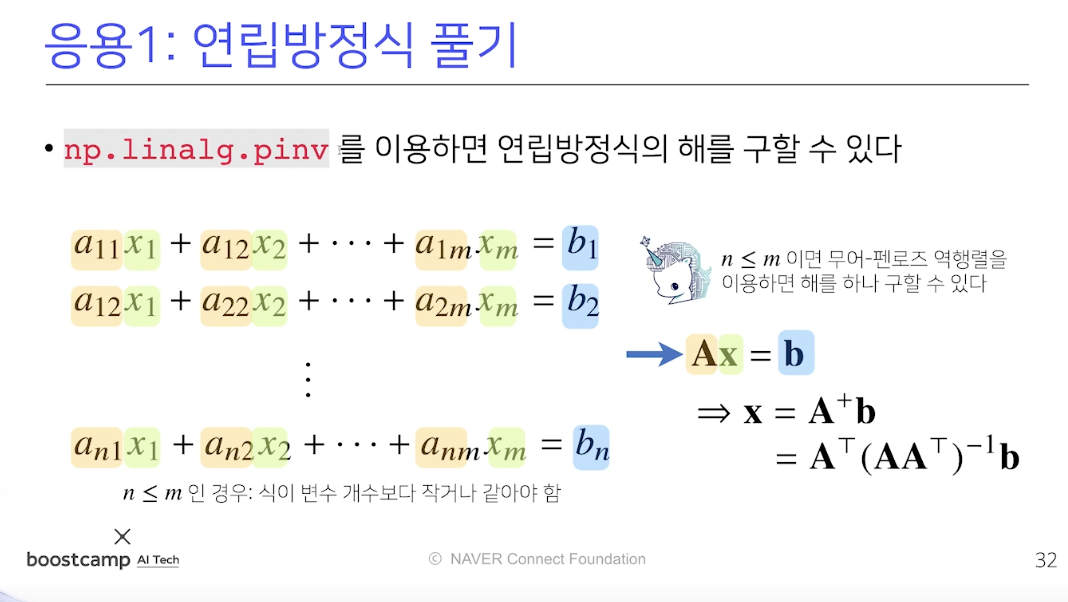
차원이 바뀐뒤 더 많은 차원으로 옮겨 졌다면, 아래와 같이 계산을 하면된다

정리.

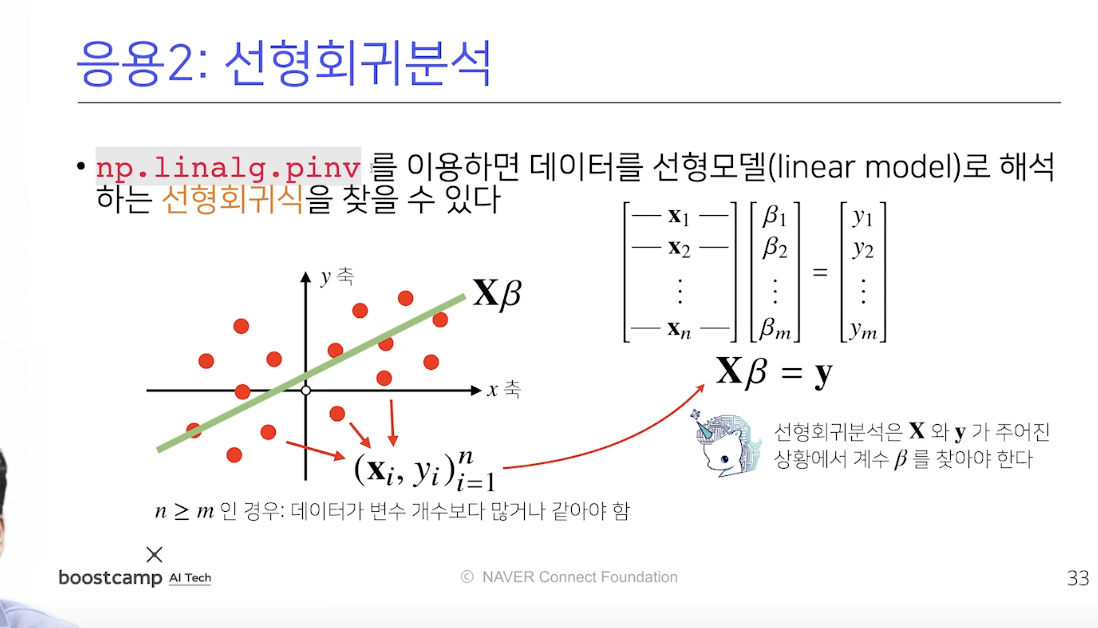
지금 까지 배운 행렬의 특징을 선형회귀분석에서 적용을하면, x라는 벡터 테이터를 입력 데터라고 생각할 수 있다.
X라는 입력 데이터에 b(대수 벡터)를 고해주면, 초록색 선으로 표현되는 선형모델을 만들수 있다.
이 때 어떤 벡터를 찾을수 있을까 라는게 선형회귀 분석이다.

우리는 이를 찾기 위해, y라는 원래의 결과값과 유사역행렬을 통해 찾게된, b(대수 벡터)*X값을 뺏을때의 값을 노름2로 바꾸었을 때 최소값이 나오는 b(대수벡터)를 찾는다.

역행렬로 구하면, ||y-y^||2의 최솟값이, X^+y를 하면 한번에, 나온다... (경사하강법에서는 여러번 계산해야함.)

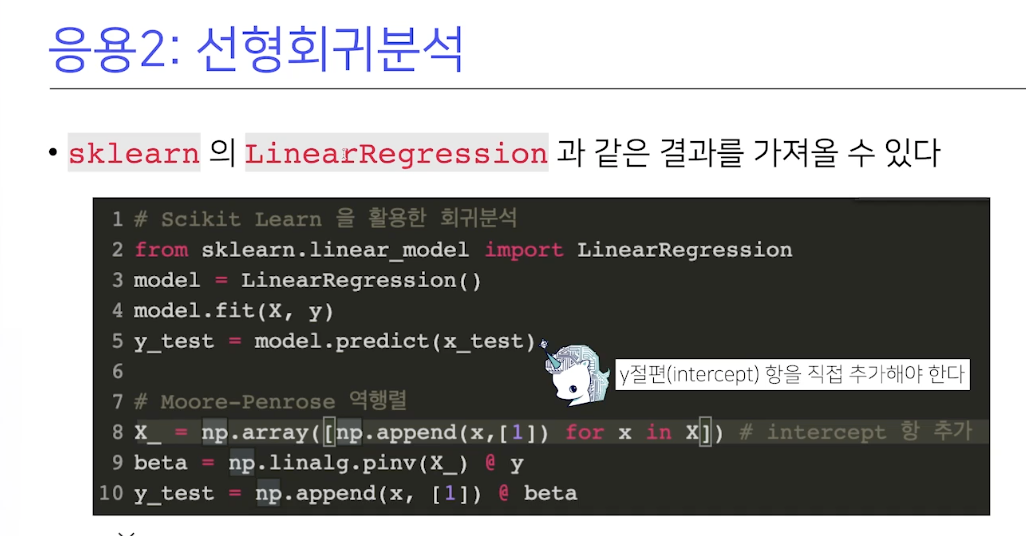
넘파이로 해보고 싶다면 아래 코드를 실행해보자.