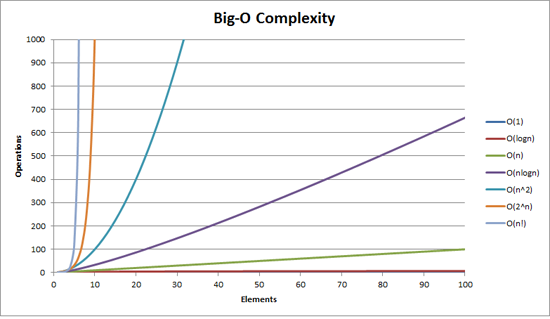
Big O Notation 이라는 것은 여러 알고리즘의 성능을 판단할 수 있는 지표
Big O Notation
Big O Notation이란 알고리즘의 복합도에 대한 상대적인 표현이며, 여러 알고리즘의 성능을 비교/판단해 볼 수 있는 지표이다. 여러 문서나 자료에서 Time complexity라는 단어를 마주하게 되는 경우가 꽤나 존재하는데, 이 Time complexity를 Big O Notation으로 표현한다.
Big O notation의 경우 O(?)와 같은 형태를 띄며 ? 안에는 결정변수 n에 관한 식이 들어간다. O(1), O(n), O(logn) 것들이 예시가 된다.
실제 코드를 살펴보자.
i = 0
for i in range(n):
i += 1
print(i)이는 for문을 통해 i+=1이 n번만큼 시행되기 때문에 단순한 O(n)의 예제이다.
i, j =0, 0
for i in range(n):
i += 1
for j in range(n):
j -= 1
print(i, j)그렇다면 이 코드의 시간 복잡도는 어떻게 될까? 첫번째 for문 내부 코드도 n번만큼 시행되고, 두번째도 동일하기 때문에 총 2n번이 실행되서 O(2n)이라고 생각했는가? 정답은 O(n)이 되며 그 이유는 Big O notation에 있다. 우리는 당연히 2n번의 시행이 n번의 시행보다 더 많은 시간을 필요로 하는 것을 안다. 하지만 Big O notation의 진정한 의미는 n이 증가할 때 실행에 걸리는 시간이 어떠한 형태로 증가하는 지를 나타낸 것이다. n이든 2n이든, n이 증가하면 동일한 비율로 계속해서 증가, 즉 선형적으로 증가하기에 O(n)으로 표기하는 것이다.
Big O notation은 n이 증가함에 따라 처리 시간의 증가하는 형태를 나타낸다!
따라서 O(kn)에서 k가 상수일 경우, 상수 k를 무시하여 O(n)으로 표기하게 된다.
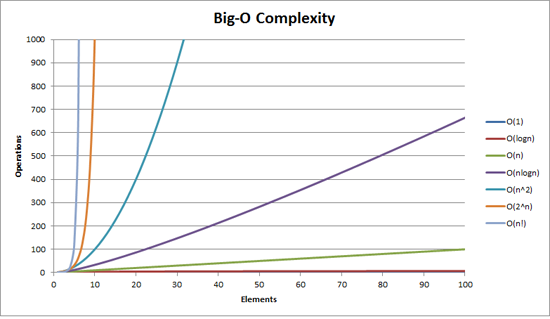
다음이 여러 O notation의 n이 커지는데에 따라 operation수가 증가하는 형태를 보여주는 그래프이다. O(n)과 O(n^2)만 봐도 차이가 확연하게 존재하기 때문에 O(kn)의 k 정도는 무시할 수 있는 것이다.
또, 추가적인 얘기로 한 알고리즘에 있어 best case, average case, worst case가 존재한다. 단순하게 list=[10, 100, 1000, 10000] 이 있다고 해보자.
-
best case = O(1) : 10을 찾을 때
list의 첫번째 아이템인 10을 찾기 때문에 list가 자신의 0번 index만 확인하고도 결과를 내게 된다. -
worst case = O(n) : 10001을 찾을 때
10001의 경우 list의 없기 때문에 list의 맨 마지막 까지 가고 나서야 존재하지 않음을 알 수 있고, O(n)만큼 걸리게 된다.
이렇듯 상황별로 알고리즘의 처리시간이 달라지며, 일반적으로 Time Complexity를 물으면 worst case에 대하여 답을 하면 된다.
with space complexity
알고리즘에는 time complexity 뿐만 아니라 space complexity 또한 존재한다. space complexity란 알고리즘 처리에 있어 메모리를 얼마나 사용하냐인데, 일반적으로 time complexity를 구할 때는 space complexity를 고려하지는 않는다. 다만 알고리즘이 점차 고도화 될 수록 time complexity 와 space complexity가 tradeoffs 관계일 수 있다는 점을 인지하고 있자!
