Bits

HEYDAY7·2021년 4월 29일

Data Structure and Algorithm

목록 보기

1/21

Bits란

binary digits로 0 혹은 1의 값을 갖는다. 전류적인 의미로는 1 : Presence, 0 : Absence 이며 각각 True, False를 나타낼 수도 있다. 하나의 Bit를 사용하여 2가지 값을 나타낼 수 있으므로, N개의 bit는 2^N개를 나타낼 수 있다!

이러한 bit를 사용하여 컴퓨터가 Data를 나타내고 그 방식을 간단히 알아보자.

Bit DataType

representation of information in bits. bit로 데이터를 나타내는 방법들이다.

단순 표시 (1진수)

단순한 bit 카운팅하는 방식으로 아래 예시를 보면 바로 이해될 것이다.
-> 5 = 11111
-> but 너무 많은 bit가 필요하게 된다.

boolean data

1은 True, 0은 False를 의미하게 된다. 이에 따라 각 bit 가 특정 조건들에 대한 T/F 값인 것으로 데이터를 저장할 수 있다.
ex)

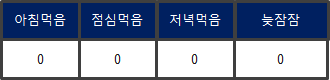
학생1 : 1100 (아침과 점심만 먹음)
학생2 : 0111 (늦잠자고, 점심과 저녁 먹음)

4가지 bit 연산

논리적인 연산이라고 생각하면 된다. 4가지의 bit 연산 NOT(~), AND(&), OR(|), XOR(^)이 있고 아래와 같다.

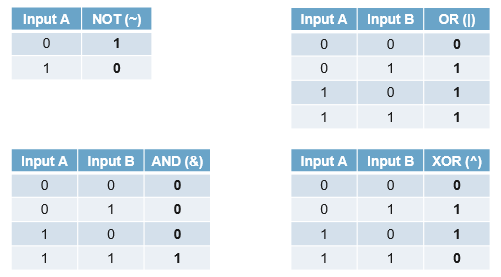
T and T = T와 같이 논리식을 bit단위로 적용시킨 것이라고 보면 된다. bit vector의 경우에는 각 자리에 대응하는 값들 끼리 bit 연산을 진행해서 결과를 내면 된다.

Representing Integers

bit로 숫자를 나타내는 여러가지 방법들이다.

부호가 없는 양수

단순히 2진수로 나타내면 된다. 2^N-1개 나타낼 수 있음. 가장 base가 되는 방법으로 이후에 부호를 나타내는 표현법에서도 양수는 이와 동일하게 표현함.

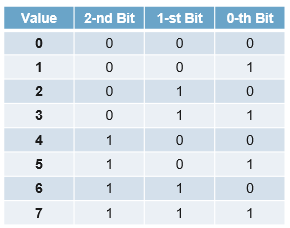
signed integer

부호가 있는 숫자이다. 맨 앞에 있는 bit가 부호를 나타내는 bit로 0 => 양수, 1 => 음수를 의미한다. 나머지 숫자들은 일반적인 2진수로 나타내면 된다.

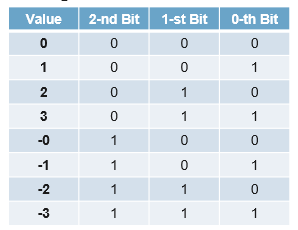
signed integer / 1's complement

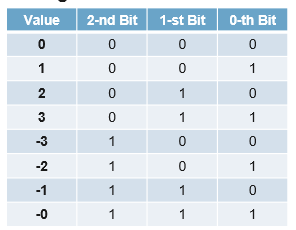1's complement의 경우 숫자의 전체 bit를 뒤집었을 때 동일한 숫자의 부호가 다른 수를 표현하게 된다. 맨 앞의 bit는 부호를 나타낸다. 2 : 010 <=> -2 : 101 이런 느낌인 것이다.

signed integer / 2's complement

일반적인 sigend integer와 1's complement에 존재하는 아래와 같은 단점을 해결하기 위해 등장.

0과 -0 두개가 존재함,
덧셈과 같은 계산이 직관적으로 이뤄지지가 않음

2's complement는 직접적으로 (X)와 (-X)를 일반적인 bit 덧셈으로 진행했을 때 0이 나오게 하는 보수를 말한다. 이 때 carry out, 즉 초과되는 자리수는 무시하게 된다.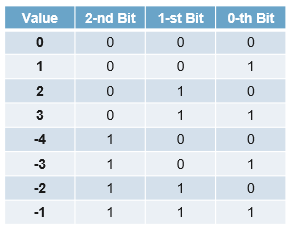 양수의 경우 일반적인 2진수와 같이 표기하면 된다. 음수의 경우 쉽게 만들어내는 방법이 있다.
1. 절대값을 2진수로 표현하고,
2. 모든 bit를 뒤집고 (0->1, 1->0),
3. 구한 상태에서 1을 더해주면 된다.

예) -2의 케이스 / 010 -> 101 -> 110

덧셈과 뺄셈

2's complement의 덧셈과 뺄셈의 경우 2가지 가정이 필요

두 숫자의 bit vector의 길이가 같다.
그 결과값 또한 동일한 길이의 bit vector로 표현될 수 있다.

덧셈 : carry out 되는 수를 무시하고 일반적인 덧셈을 하면 된다.

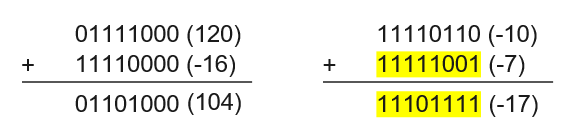
뺄셈 : 빼는 수에 -를 곱해 연산 부호를 +으로 변경시키고 덧셈을 진행한다.

만약 2's complement로 표현된 식의 계산에서 bit vector의 길이가 다를 경우 좀 더 긴 vector의 길이에 맞춰 양수에는 부족한 만큼의 0을, 음수에게는 1을 붙여주면 된다.

* 주의. 자리수가 넘는 숫자가 나올경우 잘못 표기될 수 있다. !! overflow

floating point

32 bit vector로 나타낸다. 기본 form은 다음과 같다.

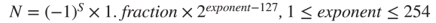
간단히 예시를 하나만 보고 넘어가자
" 1 10000011 0001 0000 0000 0000 000 " 가 있다고 하면 이 숫자를 변경시켜보자
우선 맨 처음 1은 부호를 나타내는 수로 -1, 즉 음수를 의미한다.
두번째 10000011 = 131로 자리수와 관련되어 있다. 식 대로 풀면 가운데 부분은 2^(131-127) = 2^4 = 16 이 된다. 마지막은 소수부로 초반 0001에서 1이 1/16을 의미하게된다. 따라서 위 숫자는 -1 * 16 * (1+1/16) 이 되서 -17이 나오게 된다.