Bubble Sort
이 알고리즘은 인접한 두 숫자를 반복해서 비교하며 큰 숫자가 오른쪽으로 가도록 계속해서 바꿔나가는 방식이다. 1번의 반복마다 정렬이 되지 않은 숫자들 중 가장 큰 숫자가 제일 오른쪽으로 오게 된다. 그 이유는 숫자쌍이 (0,1), (1,2) ... 이렇게 한 개씩 겹치기 때문에 가장 큰 수는 오른쪽으로 계속해서 이동하게 된다.
- visualization : visualgo
백문이불여일견이다. 아래 사이트에 방문해서 상단의 BubbleSort를 클릭하고 좌하단의 Go 버튼을 눌러 sorting 과정을 지켜보자. 이해가 훨씬 편할 것이다. 다른 sorting 알고리즘들도 확인 가능하다.
구현
def bubble_sort(arr):
for n in lange(len(arr)-1, 0, -1):
for k in lange(n):
if arr[k] > arr[k+1]:
temp = arr[k]
arr[k] = arr[k+1]
arr[k+1] = tempperformance
이 알고리즘의 time complexity는 O(n^2)이 된다. 다만 구현이 매우 간단하기 때문에 이러한 부분은 장점으로 여겨져 자주 사용되곤 한다.
Selection Sort
Bubble Sort와 유사하도록, 정렬이 되지 않은 배열에서 가장 큰(작은) 숫자를 찾아 알맞은 위치에 넣어주는 것이다. Bubble Sort와의 차이점은 값을 바꾸는 작업을 반복당 최대 한번씩만 한다는 것이다. 이 알고리즘은 가장 큰 값, 혹은 가장 작은 값 모두에 쉽게 적용 가능하다.
- Visualization : visualgo 상단의 SELECT 선택
구현
핵심 포인트는 정렬이 어디까지 되었는지를 기억하는 것이다! 아래 코드는 max를 찾아 오른쪽에서부터 정렬하는 코드이다.
def selection_sort(arr):
for n in range(len(arr)-1, 0, -1):
index_max = 0
for k in range(1, n+1):
if arr[k] > arr[index_max]:
index_max = k
temp = arr[index_max]
arr[index_max] = arr[n]
arr[n] = tempPerformance
Selection Sort 또한 O(n^2)를 띄며, memory complexity는 O(1)이여 성능이 그다지 좋지는 않으나, 메모리가 제한되어 있을 때 성능상의 이점이 있다.
Insertion Sort
Insertion sort의 원리는 sorted된 sublist가 있다고 생각을 하고, 새로운 item이 들어올 때 그 item보다 큰 item들을 모두 오른쪽으로 한칸 밀고, 생긴 자리에 해당 item을 넣는것이다. 이 경우 sublist의 길이는 하나씩 길어지게 될 것이고, 따라서 sorted sublist의 길이가 input의 길이와 같아지면 종료된다.
- Visualization : visualgo 상단의 INSERT 선택
구현
새롭게 들어오는 item을 특정하고, 한칸 씩 앞으로 가며 자신보다 큰 값의 경우 오른쪽으로 밀어주고, 자신보다 작아지거나 0번 위치에 오면 반복을 끝내준다는 사실을 코드적으로 적은 것이다.
def insertion_sort(arr):
for n in range(1, len(arr)):
cur_value = arr[n]
cur_position = n
while cur_position > 0 and arr[cur_position-1] > cur_value:
arr[cur_position] = arr[cur_position-1]
cur_position -= 1
arr[cur_position] = cur_value Performance
Time Complexity는 O(n^2) 이지만 동일한 complexity를 갖는 bubble이나 selection보다 더 빠르다.
장점으로는 이미 중간중간 정렬이 많이 되어 있다면 상당히 빠르게 진행할 수 있다.
Shell Sort (차후 내용 추가)
Insertion Sort를 이용한 변형이 Shell Sort라는 것도 존재한다.
Merge Sort
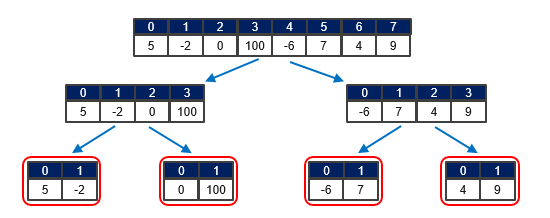
divide and conquer를 사용하는 recursive한 알고리즘이다. 주어진 array를 원소가 1개가 나올때 까지 지속적으로 반으로 쪼개고, 그 이후에 대소에 맞춰 Merge 한다!
- Visualization : visualgo 상단의 MERGE 선택
구현
divide와 merge를 생각하면 된다. help function을 이용하여 가독성을 올려보았다. 또 해당 arr를 그대로 수정하는 것이기에 function들의 parameter로 index들이 사용된다는 것이 특징이다.
def merge_sort(arr):
merge_sort_help(arr, 0, len(arr)-1)
def merge_sort_help(arr, first, last):
if first == last:
return
else:
# 반으로 나눠서 정렬해주고 (Divide)
mid = (first+last)//2
merge_sort_help(arr, first, mid)
merge_sort_help(arr, mid+1, last)
# 각 정렬된 두개의 sublist를 합치면서 정렬해준다. (Merge & Sort)
merge(arr, first, mid, last)
def merge(arr, first, mid, last):
# k는 기존 arr에서 숫자를 바꿔줄 pointer가 된다.
k = first
sub_left = arr[first:mid+1]
sub_right = arr[mid+1:last+1]
i, j = 0, 0
#각 i와 j를 통해서 sub_left와 sub_right의 값들을 비교한다.
# 즉 아래 코드는 정렬된 두개의 sub_list의 값들을 서로 비교하며 작은 것 부터
# 기존 arr에 수정해가면 넣는 것이다.
while i < len(sub_left) and j < len(sub_right):
if sub_left[i] > sub_right[j]:
arr[k] = sub_right[j]
j += 1
else:
arr[k] = sub_left[i]
i += 1
k += 1
if i < len(sub_left):
arr[k:last+1] = sub_left[i:]
elif j < len(sub_right):
arr[k:last+1] = sub_right[j:]
```
Performance
Merge Sort는 O(nlogn)이 될 것이다. 그 이유는 각각의 merge function이 O(n) 만큼 걸릴텐데, 이러한 merge function이 log(n)만큼 반복되기 때문에 다음과 같은 결과가 나오는 것이다. 다만 sub_list를 사용하는 과정에서 추가적인 memory complexity O(n)이 발생하는 것은 알고 넘어가야 한다.
Quick Sort(차후 내용 추가)
나중에 추가적으로 정리할 것 !!
구현까진 해두었다
마치며
python list에 존재하는 sort는 위에 소개한 여러 방식들보다도 빠르다. python에서 구현된 sorting은 Tim sort라고 하여 merge sort와 insertion sort를 섞은 hybrid한 알고리즘이다. 원리는 간단하게는 n이 작을 때에는 insertion sort가 merge sort보다 빠르다는 장점을 이용했다고 하며, time complexity는 O(nlogn)이다.
여러 sorting에 대해서는 추가적인 시각화의 경우 아래 링크를 참고하면 좋다.
www.sorting-algorithms.com
visualgo.net
