.svg.png)
Tree
tree, 우리가 아는 일반적인 나무에는 root(뿌리), branches(가지) 그리고 leaves(잎)이 있다. Tree datastructure 또한 이러한 기본적인 구성은 동일하고, 다만 현실과 다른 것은 root(뿌리)가 가장 위에 있는 뒤집어진 형태라는 것 뿐이다.
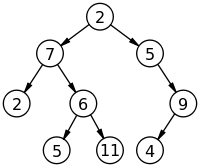
(출처 위키피디아)
Tree에서 사용하는 용어
-
Node
위 그림상으론 원 하나를 의미하며 추가적으로 key(value)를 갖는다. -
Edge
edge가 두 node를 이어주는 역할을 한다. root를 제외한 모든 node는 1개의 incoming edge와 여러개의 outgoing edge를 가지고 있다. -
Path
ordered list of nodes로 root에서부터 특정 node까지 edge로 연결된 경로를 뜻한다. -
children
parent 기준 outgoing edge와 연결된 모든 node들을 칭한다. -
parent
child 기준 자신의 incoming edge와 연결된 node를 칭한다. -
siblings
child node에서 사용될 수 있는 단어로, parent가 같은 다른 node들을 말한다. -
Leaf Node
가장 아래에 있는, children이 없는 node를 의미한다. -
Level
root 기준 몇 번 아래로 내려왔는지를 의미한다. 즉 상단의 이미지의 경우 11은 level 3가 될 것이다. -
Height
maximum level : 제일 깊은 level
Tree 특징
- 각 node가 갖는 path는 유일하다.
- tree는 subtree 들로 구성되어 있다. (recursive한 알고리즘 적용이 가능하다는 뜻이다.)
- 한 node는 다른 parent, child를 제외한 node들과 독립이다. 즉 cycle이 존재하지 않는다.
- hierarchical(계층적) 구조를 갖는다.
예시) file system, webpage(HTML)
Tree의 여러 종류
Binary Tree
2진 트리의 경우 단순히 한 node가 최대 두 개의 child를 가질 수 있는 경우를 의미한다. Binary Tree 중 아래 세가지를 보고 넘어가자
-
Complete Binary Tree
마지막 level을 제외하고 모든 level의 node가 꽉 차 있으며, 마지막 level의 경우 node가 왼쪽에서 오른쪽으로 차례차례 채워져 있어야 한다.
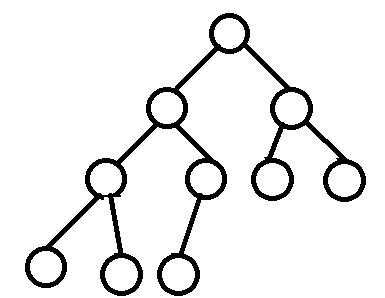
-
Full Binary Tree
leaf node를 제외한 모든 node가 2개의 children을 갖고있는 Tree를 의미한다.
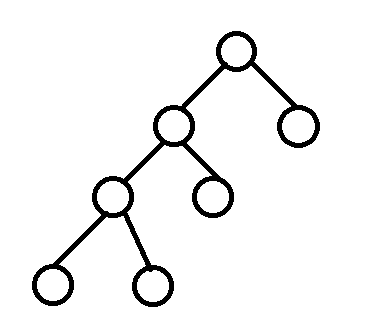
-
Perfect Binary Tree
말 그대로 모든 level의 node가 꽉 차있고, 마지막 level을 제외한 모든 node들이 두 개의 children을 갖고있게 된다. 1번과 2번을 합한 느낌이라 보아도 된다.
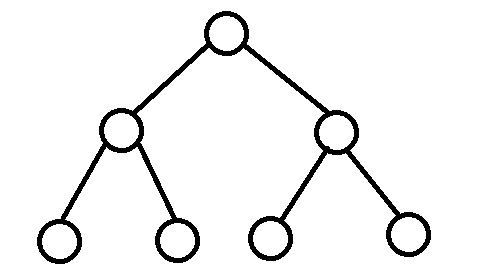
Binary Search Tree
BST는 실질적으로 구현되어 사용되는 경우도 꽤나 있기에 따로 정리하였다. 이 글을 참고하면 된다.
Binary Heaps
Binary Heap 에서는 complete binary tree를 사용한다. 이 complete binary tree란 마지막 level을 제외하고는 모든 node가 차 있는 binary tree를 뜻하고 가장 큰 특징은 list 하나만 있으면 tree를 표현할 수 있으며, 자식과 parent의 관계를 숫자적인 관계로 나타낼 수 있다는 점이다.
python에서 binary heap을 나타내면 list를 이용하는데 list의 0번 index는 0으로 고정한다. 이는 계산의 편의를 위함이다. 그 이후에는 root부터 한 level씩 내려오며 등장하는 원소들을 순서대로 적어넣게 된다. 예시는 아래와 같다.
* (출처: 위키피디아)
이 tree를 binary heap으로 나타내면
[0, 1, 2, 3, 17, 19, 36, 7, 25, 100]이 된다.
이러한 binary heap은 두가지 종류가 있다. min heap과 max heap이다. min heap이 가지는 특징은 모든 parent는 자신의 child보다 작아야 한다는 것이며, max heap의 경우는 그 반대이다. 즉 상단의 예시는 min heap이라고 할 수 있다.
수학적 특징
child와 parent간의 index 관계가 존재한다.
index가 i인 node가 존재한다고 하자. 이 경우 i의 left child의 index는 항상 i X 2, i의 right child는 i X 2 + 1 가 된다. 예외는 없기에 저 index의 값이 없다는 것은 child가 존재하지 않는다는 의미이다!
위에 주어진 예시에서 생각해보면 2 node의 child는 17 node와 19 node인데 각각의 index는 2, 4(2x2), 5(2x2+1)인 것을 볼 수 있다.
Tree Traversal
크게 두가지로 나눠준다. 바로 Breadth-First Traversal과 Depth-First Traversal이다. 이 두가지로 크게 나눠 살펴보자. 이해를 돕기 위해 바로 아래 예시를 가지고 계속해서 진행한다.
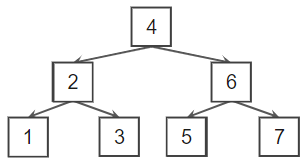
기본 코드는 아래와 같고, traversal method를 추가해 나갈 것이다.
class TreeNode:
def __init__(self, val, k):
self.val = val
self.arity = k #child의 수를 나타낸다.
self.child = [None] * k #child list
class Tree:
def __init__(self, root=None):
self.root = root
def visit(self, node):
print(node.val)tree1 = TreeNode(1,2)
tree2 = TreeNode(2,2)
tree3 = TreeNode(3,2)
tree4 = TreeNode(4,2)
tree5 = TreeNode(5,2)
tree6 = TreeNode(6,2)
tree7 = TreeNode(7,2)
tree4.child[0] = tree2
tree4.child[1] = tree6
tree2.child[0] = tree1
tree2.child[1] = tree3
tree6.child[0] = tree5
tree6.child[1] = tree7
tree = Tree(tree4)BFT
Breadth-First, 즉 가로로 훑으면서 내려가는 것이라고 이해하면 쉽다. 키워드로 이해하자만 좌에서 우로, 위에서 아래로 라고 생각하면 쉽다. 코드를 봐보자
def BFT(self):
#base case
if self.root is None:
return
q = [self.root]
while q:
curNode = q.pop(0)
self.visit(curNode)
for child in curNode.child:
if child:
q.append(child)q 라는 queue를 두어 관리하고, breadth first를 구현하기 위해 각 child를 queue에 넣고, pop으로 빼는 형식을 사용하였다.
이 경우 tree.BFT()를 실행해보면 4, 2, 6, 1, 3, 5, 7 순서로 print 되는 것을 볼 수 있다.
deque를 이용하면 q 를 구성하면 push와 pop을 좀 더 편리하고 빠르게 작동시킬 수 있다.
DFT
Depth-First, 말 그대로 깊이를 먼저 탐색하는 방법이다. 이 DFT 안에도 세가지 방식이 존재하며, 그 차이는 tree에서 root를 언제 방문하게 할 것인가 이다.
preorder : root(parent)를 최우선으로 방문한다.
def __DFT_preorderHelp(self, curNode):
#base case
if curNode is None:
return
#recursive case
self.visit(curNode) #현재 tree의 root이 curNode를 먼저 방문
for child in curNode.child: #이후 child 방문
self.__DFT_preorderHelp(child)
def DFT_preorder(self):
self.__DFT_preorderHelp(self.root)이 경우 tree.DFT_preorder()를 실행하면 4, 2, 1, 3, 6, 5, 7 순서로 print 되는 것을 볼 수 있다.
이러한 preorder traversal은 directory listing과 같이 순차적으로 안으로 파고들어야 하는 경우에 유용하게 쓰인다.
inorder : root(parent)를 child 방문하는 중간에 방문
def __DFT_inorderHelp(self, curNode):
#base case
if curNode is None:
return
#recursive case
for i in range(len(curNode.child)):
if i==1: #첫번째 child 이후에 visit
self.visit(curNode)
self.__DFT_inorderHelp(curNode.child[i])
def DFT_inorder(self):
self.__DFT_inorderHelp(self.root)이 경우 tree.DFT_inorder()를 실행하면 1, 2, 3, 4, 5, 6, 7이 나온다.
이 inorder traversal의 경우 tree 전체를 list로 flatten 할때 사용하기 유용하다.
postorder : 자식들을 모두 방문한 후에 root(parent) 방문
def __DFT_postrderHelp(self, curNode):
#base case
if curNode is None:
return
#recursive case
for child in curNode.child: #child 방문
self.__DFT_preorderHelp(child)
self.visit(curNode) #이후에 현재 tree에 root를 나중에 방문
def DFT_postorder(self):
self.__DFT_postorderHelp(self.root)마지막으로 tree.DFT_postorder()를 실행하면 1, 3, 2, 5, 7, 6, 4 순으로 print 된다.
마무리
이렇게 여러 종류의 tree와 tree traversal 방식에 대해 알아보았다. 이를 모두 직접 해 볼 필요는 없지만, 한번 따라 적어보면 그 논리를 이해하기 훨씬 쉬울 것이다.
