Linear-Time Selection
Quick Sort의 최악의 경우는 언제 발생하는가?
바로 pivot을 항상 가장 큰 값이나 가장 작은 값으로 잡을때이다.
이 경우 시간복잡도는 Θ(n²) 가 된다.
이러한 경우를 피하기 위해, 우리는 Pivot을 잘 설정하자는 목표를 가지고
Linear-Time Selection(선형 시간 선택) 알고리즘을 사용할 것이다.
Finding the Min and Max

리스트의 길이가 n일때, 최솟값과 최댓값을 찾기위해선 전체요소를 한번씩만 훑으면 된다.
따라서 시간복잡도는 O(𝑛)이 된다
Finding the 𝒌-th smallest element (naive)

그렇다면 입력배열에서 k번째로 작은 수를 찾는 방법은 어떨까?
사진에서 보는 것처럼 Naive하게 Mergesort로 정렬을한 후 k번째 원소를 리턴한다면
전체 시간 복잡도는 Θ(nlogn) 이 된다. 즉, 정렬하는데 시간의 대부분을 잡아먹는다는 것
이는 Linear-Time Selection이란 이름과 달리, 절대 선형 시간이 아니다!
진짜 Linear-Time Selection을 하려면 더 똑똑한 방법이 필요하다는 것이다.
🔥 Quick Select
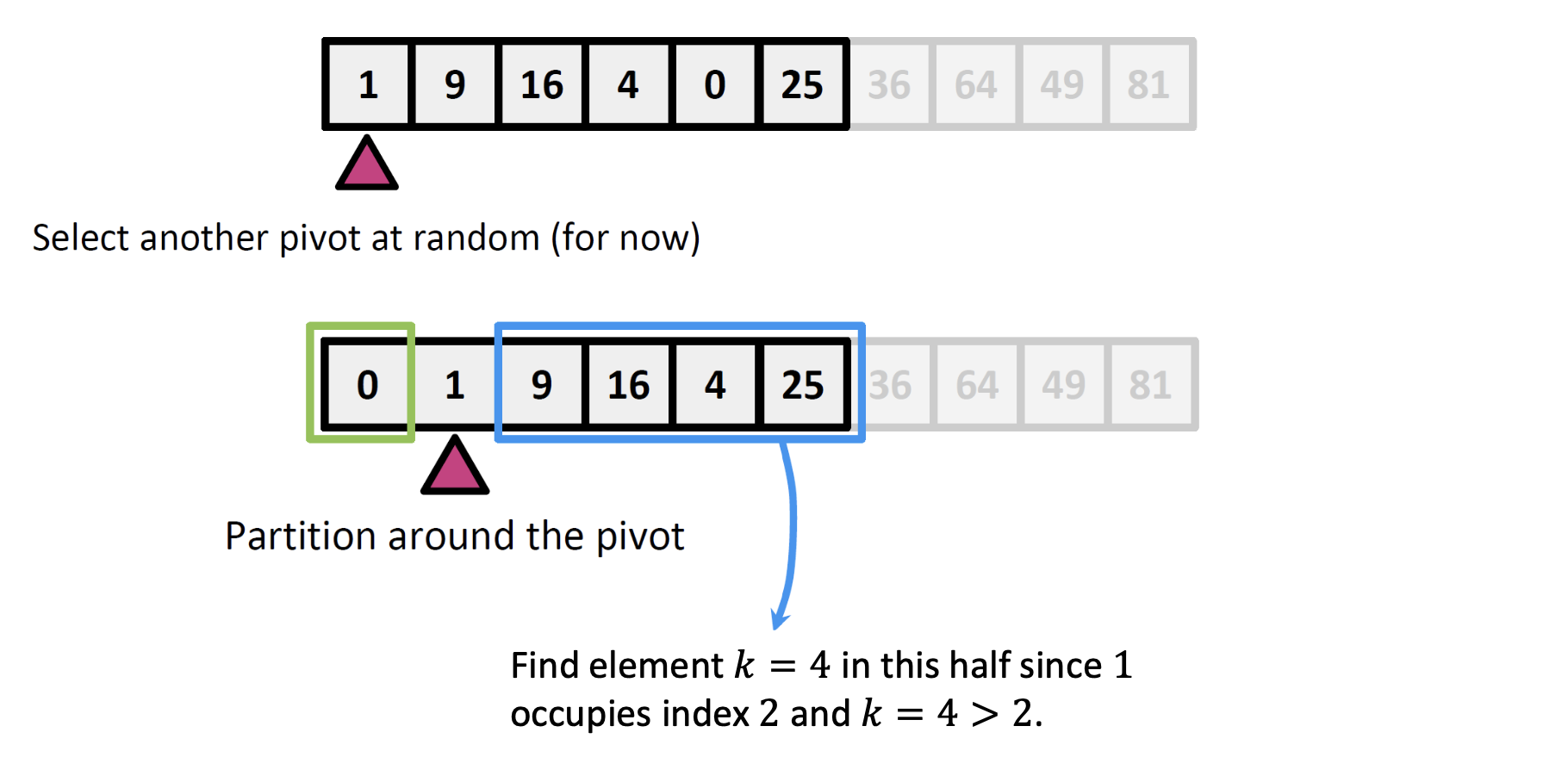
다음 그림은 Quick Select의 핵심 아이디어를 보여주는 장면이다.
우리의 목표는 k = 4번째로 작은 값을 찾는 것이다.
(즉, 정렬된 배열에서 4번째 위치에 있는 값을 원함)
⚙️ Step by Step
그림을 따라 퀵 선택의 순서를 살펴보자.
1. Pivot 선택
아무거나 하나 골라서 pivot으로 삼는다.
예시에서는 36을 pivot으로 고름 (랜덤 선택이라고 가정)
2. Partition (분할)
36보다 작은 값들은 왼쪽,
36보다 큰 값들은 오른쪽으로 보내서 배열을 나눔.
3. pivot의 위치는 몇 번째인가?
→ 이 그림에서 보면, 36은 7번째 위치에 있다 (index 7)
4. 내가 찾고 싶은 k = 4는 어디에 있어야 할까?
k = 4 < 7이므로, 원하는 값은 왼쪽 그룹에 있다!
그래서 오른쪽 그룹은 아예 무시하고
왼쪽 그룹에서 다시 Quickselect를 재귀 호출한다.
우리가 흔히 아는 퀵정렬의 메커니즘이지만
Quickselect는 pivot 기준으로 절반씩 날려가며
필요한 쪽만 정렬 후
탐색하니 → 평균 O(n)에 가능함!
Pseudo code
SELECT(A, p, r, k)
if p == r:
return A[p] // 부분 배열의 길이가 1이면, 그 하나뿐인 값이 정답임
q = RANDOMIZED_PARTITION(A, p, r)
# A[p...r] 구간을 파티션하고, q는 피벗의 최종 위치
# 즉, A[q]는 정렬했을 때 이 구간에서 몇 번째로 작은 값인지 정해짐
i = q - p + 1
# i는 A[q]가 A[p...r]에서 몇 번째로 작은 값인지를 의미
# p부터 q까지 i개의 원소가 있으니까 i = q - p + 1
if k == i:
return A[q] // 우리가 찾고 있는 k번째 작은 값이 바로 피벗 A[q]라면 그걸 반환
elif k < i:
return SELECT(A, p, q - 1, k)
# 우리가 찾는 값은 피벗보다 왼쪽에 있음
# 그러니까 왼쪽 부분 배열 A[p...q-1]에서 k번째 작은 값 찾기
else:
return SELECT(A, q + 1, r, k - i)
# 우리가 찾는 값은 피벗보다 오른쪽에 있음
# A[q]까지 i개의 원소는 이미 제외되었으므로
# 오른쪽 A[q+1...r]에서 k - i 번째 작은 값 찾기
Induction (귀납적 증명)
그렇다면 이 알고리즘이 제대로 작동하는지 알아보자.
지금껏 우리는 정당성을 증명할때, Loop invarient을 사용했다.
하지만 이번엔 Induction, 즉 귀납법을 사용해 증명해볼 것이다.
우선 귀납적 증명에는 총 4가지 요소가 있다
1. Inductive Hypothesis (귀납 가정)
알고리즘이 길이 1부터 n까지의 입력 리스트에 대해서 잘 동작한다고 가정한다.
👉 이건 임시로 믿는 가정이다. 마치 "n개까지는 잘 된다고 치자!" 하고 출발하는 것이다
2. Base Case (기초 단계)
입력 리스트의 길이가 1일 때, 알고리즘이 제대로 작동함을 보임.
👉 이건 출발점이다. 예를 들어 길이 1짜리 배열에서 k번째 작은 값은 그 자체니까, 무조건 정답!
3. Inductive Step (귀납 단계)
만약 알고리즘이 길이 1부터 i까지의 리스트에서 잘 동작한다면,
길이 i + 1인 리스트에서도 잘 동작함을 보인다.
👉 이게 핵심. i까지 잘 되면 i+1도 잘 된다는 걸 보이면
→ 1부터 n까지 전부 다 잘 된다는 걸 이끌어낼 수 있음.
4. Conclusion (결론)
만약 알고리즘이 길이 n인 리스트에서 잘 작동하면,
전체 리스트에서도 항상 작동한다고 결론 내릴 수 있다.
👉 결국 우리가 원하는 말은 이것이다:
“언제 어떤 입력을 넣어도 올바르게 작동한다”
Proving Correctness
그렇다면 이제 귀납적 증명을 이용해 퀵 선택의 정당성을 증명해보자.
1. Inductive Hypothesis (귀납 가정)
길이가 n인 배열 A와 정수 k ∈ {1, ..., n}이 주어졌을 때,
SELECT(A, k)는 A에서 k번째로 작은 원소를 반환한다고 가정한다.
2. Base Case (기초 단계)
배열의 크기가 1일 때, 가능한 k는 오직 1 하나뿐.
즉 SELECT(A, 1)은 배열 A의 가장 작은 값, 즉 A[1] 자체를 반환해야 함.
📌 이때 알고리즘의 동작을 보면
if p == r: return A[p]
이기 때문에, A의 유일한 원소를 반환함.
즉, 정확히 우리가 원하는 동작을 한다는 것이 입증됨.
✔️ 따라서 base case에서도 알고리즘은 정확하게 동작하고,
이는 Inductive Hypothesis가 n = 1일 때도 성립함을 보이는 것이다.
3. Inductive Step (귀납 단계)
이제 i ≥ 2일 때, 길이 i보다 작은 모든 배열에서는 잘 동작한다고 가정하고, 길이 i에서도 잘 작동하는지 보여줘야한다.
🔍 Case 1: |L| = k - 1 인 경우
즉, pivot 왼쪽에 정확히 k - 1개의 원소가 존재한다면?
그럼 p보다 작은 원소가 정확히 k - 1개니까
p는 정렬했을 때 정확히 k번째 원소일 수밖에 없음!
📌 그래서 이 경우엔 그냥 pivot p가 정답이다.

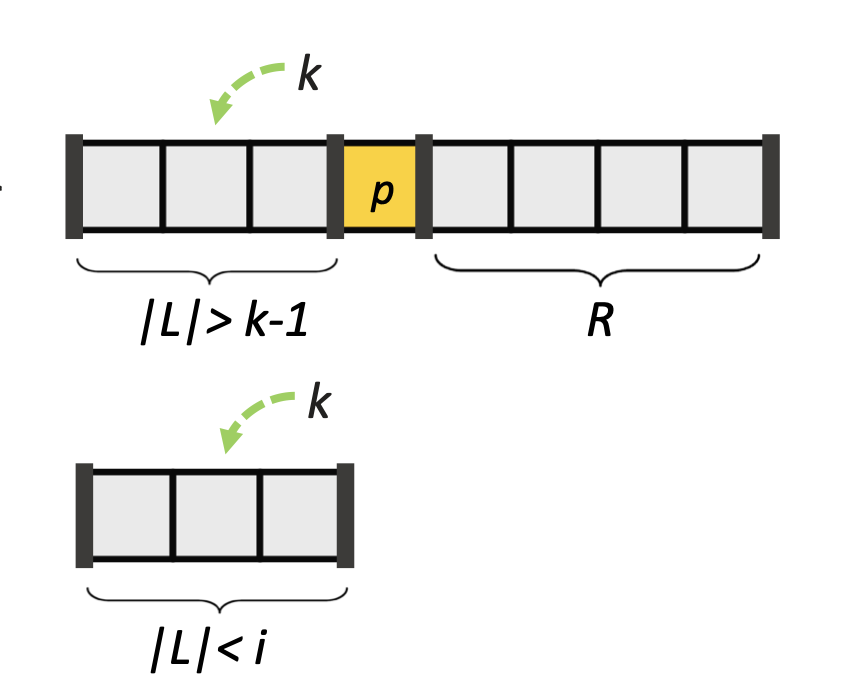
🔍 Case 2: |L| > k - 1 인 경우
|L| > k - 1, 즉 pivot보다 작은 원소가 k번째 원소보다 더 많다.
그 말은 k번째로 작은 원소는 왼쪽 서브배열 L 안에 있다는 뜻이다.
-> 지금 우리는 크기 i짜리 배열에서 동작을 증명하려는 중인데,
왼쪽 서브배열 L의 크기는 |L| < i이므로, 귀납 가정을 적용할 수 있다.
👉 즉, SELECT(L, k)를 호출하면 확실히 정답인 k번째 작은 원소를 리턴해준다는 것.
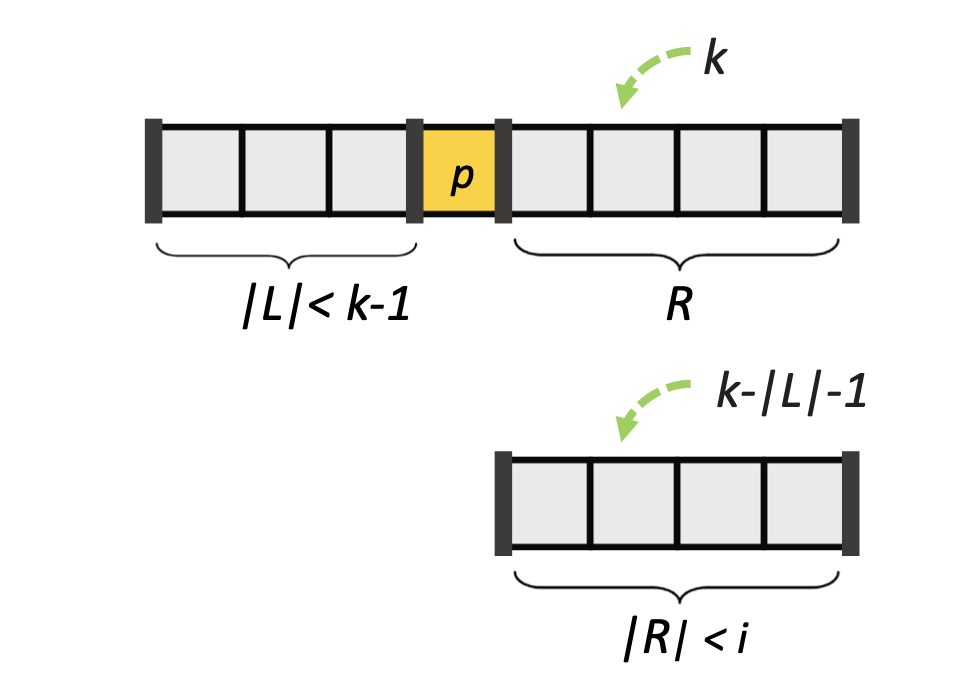
🔍 Case 3: |L| < k - 1 인 경우
이제 우리는 오른쪽 부분 배열 R에서 (k - |L| - 1)번째 작은 원소를 찾으면 된다.
왜 -1도 빼주냐? → pivot도 전체 정렬에서 한 자리 차지하니까!
그래서 전체에서 k번째 원소는 R에서는 (k - |L| - 1)번째 원소임.
중요한 건 R의 크기 < i이므로, 귀납 가정 적용이 가능하다
이제 Case 1, 2, 3까지 모두 귀납 가정으로 정당성 증명이 완성되었다.
4. Conclusion (결론)
귀납법에 의해, 위의 가정이 모든 n ≥ 1에 대해 성립함을 알 수 있다.
즉, 모든 크기의 배열 A와 k에 대해 SELECT(A, k)는 정확하게 k번째 작은 값을 찾아준다.
따라서 이 알고리즘 SELECT는 정당하다(correct)!
Runtime
이제 이 알고리즘이 잘 작동한다는 것은 귀납법으로 잘 증명하였다.
그렇다면 이 랜덤 선택(퀵 선택) 알고리즘은 충분히 빠를까?

기본적으로 partition, 즉 피봇을 기준으로 크고 작음을 비교할때
배열의 모든 요소를 한번 훑기에, partition과정에서 O(n) 이 걸린다
그 다음 피봇의 위치에 따라 왼쪽, 혹은 오른쪽만 재귀호출한다.
병합 정렬과 퀵선택간의 핵심포인트는 다음과 같다
병합정렬(Merge Sort)은 항상 양쪽 재귀 → T(n) = 2T(n/2) + O(n) → O(n log n)
Quickselect는 한쪽만 재귀 → 평균적으로 T(n) = T(n/2) + O(n) → O(n)
👉 즉, Randomized Select는 평균적으로 선형시간 O(n)에 동작한다.
하지만, pivot이 매번 나쁘게 선택되면 O(n^2)까지도 갈 수는 있다. (편향된 경우)
✅ 이상적인 경우 (Ideal case)
만약 우리가 데이터를 정확히 반으로 나눌 수 있다면
T(n) = T(n/2) + O(n)
T(n/2) : 한쪽 반만 재귀 호출
O(n) : 파티셔닝 비용 (pivot을 기준으로 분할하는 작업)
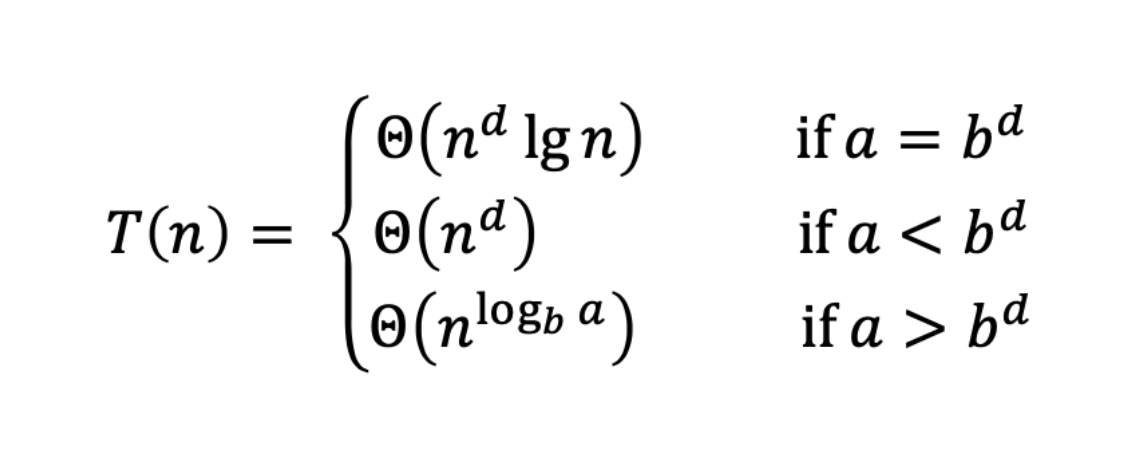
다음과 같이 마스터 정리에 따라서 case3이 적용되고, 따라서
a=1, b=2, d=1 이고, a < bᵈ 이므로 Θ(nᵈ) = Θ(n)이 된다
따라서 T(n) = O (n)
❌ 운이 엄청 나쁘면 (Worst case)
만약 항상 pivot이 제일 작거나 커서 한쪽만 채워진다면
T(n) = T(n-1) + O(n)
이 경우, 마스터 정리가 적용 불가능하므로 직접 전개해본다면
첫 번째 호출: O(n)
두 번째 호출: O(n−1)
...
마지막 호출: O(1)
따라서 T(n)=O(n+(n−1)+(n−2)+⋯+1)=O(n²) 이된다
그리고 당연히 우리는 Worst Case에 집중해야할 것이다.
그리고 이 case를 발전시키기 위해 더 좋은 피벗을 설정하는 방법을 다음 시간에 배워보자!
