더 좋은 피봇을 고르는 방법

우리가 관심 있는 건 Linear-Time Selection 알고리즘이니까, 시간 복잡도가 Θ(n) 이 되도록 피벗을 잘 골라야 한다.

그렇다면 가장 이상적인 상황은 무엇일까?
당연히 피벗이 리스트를 정확히 반으로 나눠주는 경우 일것이다.

이런 경우 분할 정복에서 항상 balanced하게 나뉘니까 Quicksort든 Select든 모두 시간 복잡도가 좋아진다.

그렇다면 이상적인 피벗이란, 리스트를 반으로 나눠주는 값, 즉 중앙값(median)임을 알수있다.
실제로, 꼭 정확한 median이 아니더라도 그것과 가까운 값이라면 충분히 좋은 성능을 낼 수 있다.

---

A Good Enough Pivot

위에서 말했듯이, 정확하게 절반으로 분할한다는 것은 현실적으로 힘들다.
따라서 현실에서는 대략 다음 정도로만 나뉘면 괜찮다고 본다.

즉 3대7정도로만 나뉘면 괜찮다는 것!

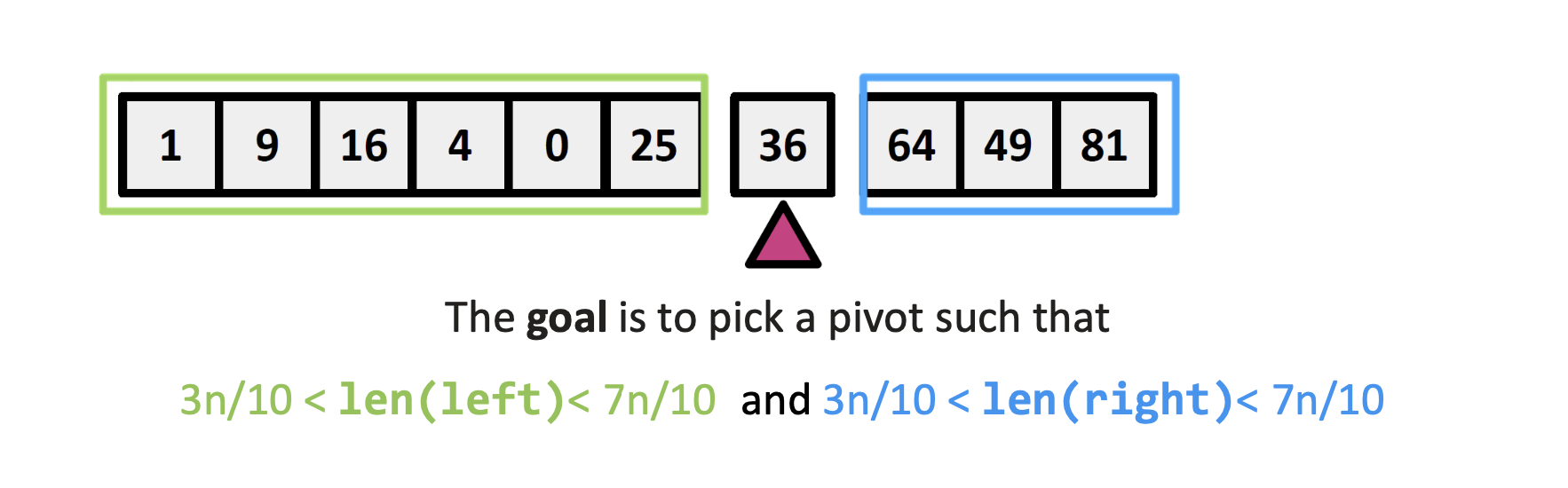
그림을 보면, 36을 피벗으로 설정하였고, 전체 배열이 대략 6:3 비율로 나뉘어진다
둘다 3~7사이니까 충분히 acceptable하다라고 볼 수 있다!

이렇게 균형적인 분할을 하게되면 재귀식은 다음과 같아진다

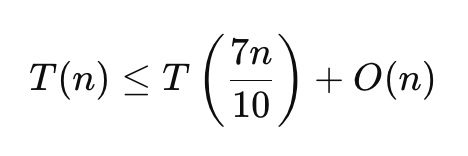
이쯤되면 습관적으로 마스터 정리가 적용이 가능한 조건임을 알 수 있어야한다.

마스터 정리를 하면 T(n) = O(n)이 된다.

---

How to get median

전체 배열에서 정확한 중앙값(median) 을 선형 시간에 직접 찾는 건 어렵다
그냥 median(A)을 구하라고 하면 정렬이 필요하고, 그건 O(nlogn) 걸리기 때문이다

하지만, 작은 리스트에서는 median을 금방 구할 수 있다.
→ 그래서 전체 리스트를 작은 그룹들로 쪼개고, 그 안에서 median을 구한 다음,
그 median들의 median을 다시 구하면 진짜 median과 비슷한 값이 나온다!

---

How to get Median of Medians

지금부터 중앙값의 중앙값, 즉 Median of Medians를 구하기 위한 3가지 단계에 대해 알아보자.
Median of Medians는 너무 기니 대충 MoM으로 줄여쓰겠다.

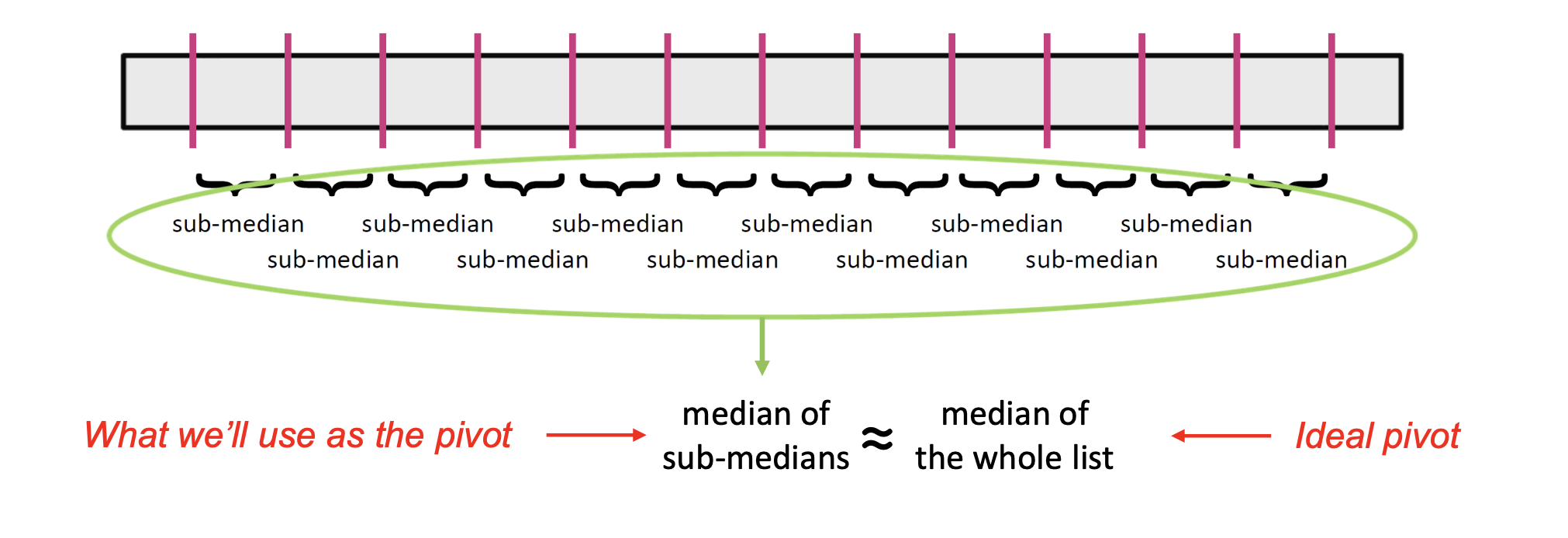
🧩 구체적인 3단계 전략

기본적인 아이디어는 다음과 같다.

1. 원래 리스트를 작은 그룹들로 나눈다 (보통 5개씩 나눈다)
   예: 길이 100이면 → 20개의 그룹 생김

2. 각 그룹에서 median(중앙값)을 구한다
   이건 그룹이 작기 때문에 그냥 정렬해서 구하면 된다 == 상수시간안에 끝나니 걱정 ㄴㄴ
   예: [5, 1, 3, 4, 2] → 정렬 → 중앙값은 3

3. 이 sub-median들의 median을 다시 구한다
   이 MoM이 우리가 피벗으로 사용할 값이다
   이 값은 전체 리스트의 median과 일치할 확률은 낮지만 상대적으로 매우 가깝다
   → 그러므로 좌우로 나누었을 때 비율이 너무 한쪽 치우치지 않는다는 장점을 가진다
   

---

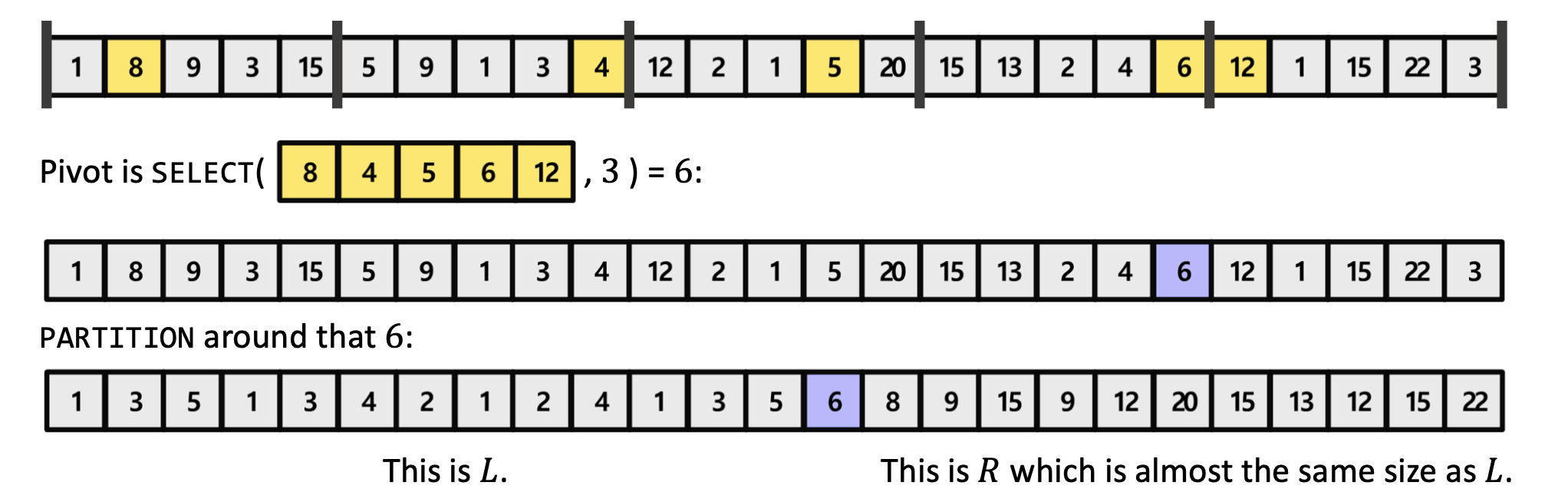
Median of Medians Algorithm

이 MoM 알고리즘의 의사코드는 다음과 같다

MEDIAN_OF_MEDIANS(A):
    Split A into m = ⌈n/5⌉ groups, of size <= 5 each # A를 5개씩 끊어서 여러 그룹으로 나눔

    for i = 1 to m:
        Find the median within the i-th group, call it p_i  #각 그룹의 중앙값을 찾음

    p = SELECT([p₁, p₂, ..., pₘ], m/2)   #sub-median들의 중앙값
    return p

이제 우리는 Select과정에서 Random partition대신 MoM알고리즘을 사용할 수 있다.
대충 보기만해도 감으로 Runtime이 빨라졌음은 느껴지지만, 얼마나 빨라졌는지 확인해보자

---

Runtime of MoM Algorithm

Runtime을 분석하기 위해 가장 핵심이 되는 논리는
"Median of Medians보다 작은 값은 최소 몇 개?"라는 아이디어이다.

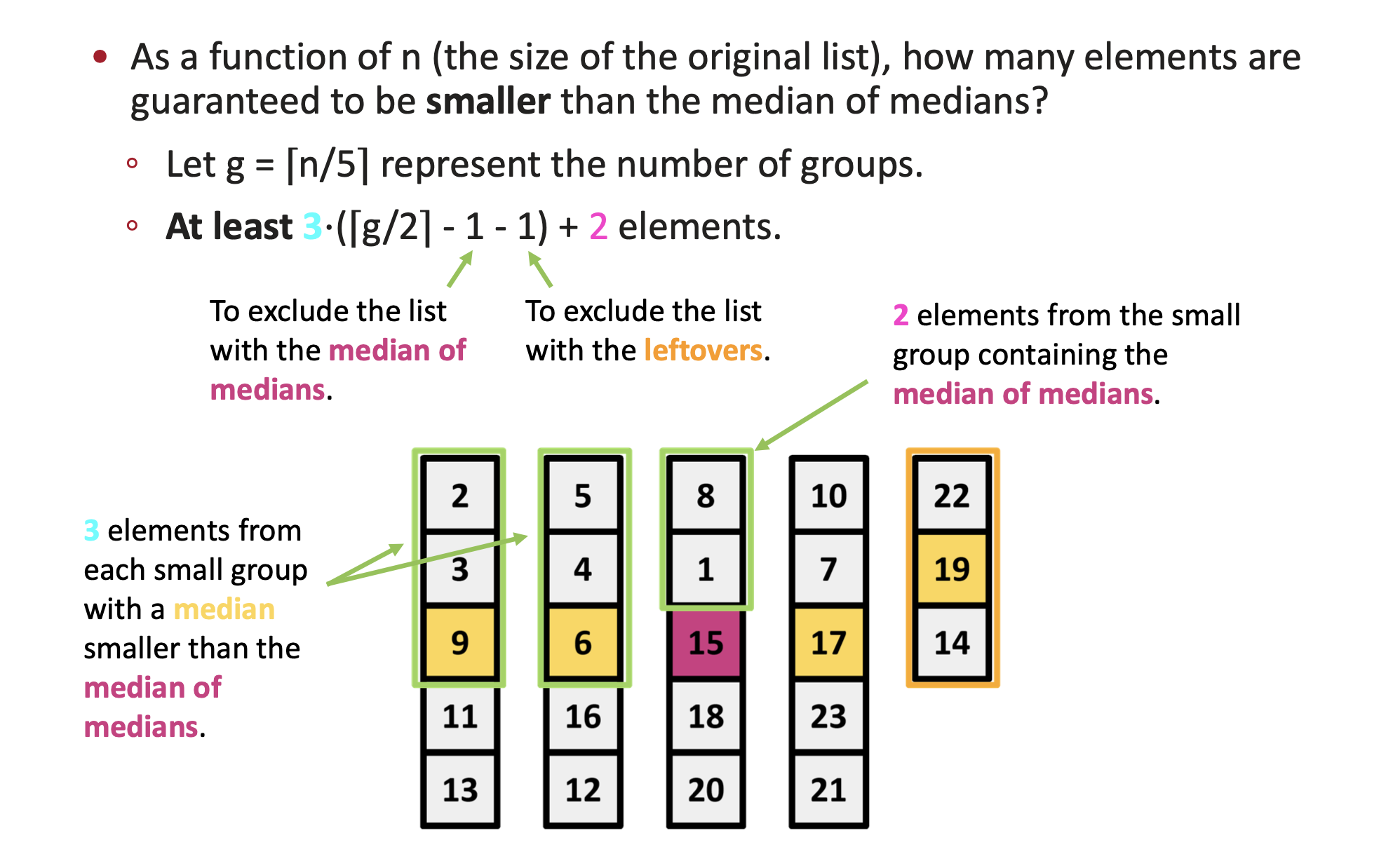
그림만 봐도 머리가 아파진다. 하지만 천천히 따라가보자
우선 n =개의 입력을 5개씩 그룹으로 나누었을때, 그 그룹의 갯수를 g라고 하자

그렇다면 g = ⌈n/5⌉이 될것이다. ([] 중괄호가 아니다, ⌈⌉ceiling 기호이다)

아무튼, 각 그룹에서의 median들을 구하고 그 medians들의 median이 pivot이 된다.

이제 그림 속 식을 이해하기 위해 점층적으로 단계를 나누어 설명해 줄 것이다.

① ⌈g/2⌉ : pivot은 g개의 sub-median 중 중앙값이므로, 왼쪽 절반에 최소 ⌈g/2⌉개의 서브‑미디언이 있다.

② ⌈g/2⌉ - 1 그런데 이 ⌈g/2⌉개 안에는 ① pivot이 들어 있는 그룹이 포함되어 있다. → 이 그룹은 따로 처리해야 하므로 1개 제외.

③ ⌈g/2⌉ - 1 - 1 또, g가 5의 배수가 아니면 끝에 원소가 5개 미만인 “leftover”이 한 개 생길 수 있다. 이 그룹의 서브‑미디언은 정확히 가운데가 아니다. → 추가로 1개 제외 (물론 g가 5의 배수가 될 수 있으나, 우리는 일반화를 위해 최대한 보수적으로 최소값을 구할 것이다.)

④ 3 · (⌈g/2⌉ - 1 - 1)남아 있는 각 정상적인 그룹에서는 ‘ sub-median < 최종 pivot’인 그룹마다 최소 3개(a₁, a₂, a₃)가 pivot보다 작음이 보장된다. → 그룹당 3개씩 곱해 준다.

⑤ + 2마지막으로 pivot이 들어 있는 그 그룹에서도 pivot보다 작은 원소가 정확히 2개 존재한다

최종적으로 MoM보다 작은 원소는 최소 3⋅(⌈g/2⌉- 1 - 1) + 2 개 이상이다

---

이렇게 MoM보다 작은 원소가 최소 몇개 있는지 확인했다면,
MoM보다 큰 원소가 최대 몇개 있는지도 쉽게 알 수 있다.
pivot 1개를 제외한다면 나머지 원소의 수는 n -1
n -1 에서 아까 구한 [3⋅(⌈g/2⌉−2)+2]을 빼준다.

=n−1−3⌈g/2⌉+6−2
=n−3⌈g/2⌉+3
위 식을 단순화 해보자

최종적으로 MoM보다 큰 원소는 최대 0.7n + 3개에 불과하다

---

위 식은 pivot = median of medians 로 분할했을 때
왼쪽·오른쪽 부분배열의 크기가 “ 최소 30 % – O(1) / 최대 70 % + O(1) ” 범위에 묶인다는 사실을 정리한 것이다.

---

Runtime analysis

이 알고리즘의 시간복잡도의 점화식은 다음과 같다.

T(n) ≤ T(n/5) + T(7n/10) + O(n)

일단 점화식이 나오면 아묻따 마스터정리 조건을 만족하는지 확인해라
아쉽게도 조건을 만족하지 않는다.
그럼 Substitution Method를 쓸 수 밖에 없다

---

🔵 Step 1: Guess the Answer

우리는 다음과 같이 답을 추측해볼 수 있다: T(n)=O(n)

🔵 Step 2: Formal Proof (Substitution Method)

Inductive Hypothesis (귀납 가정)

모든 $1 \leq k < n$에 대해

$T(k) \leq Ck$

Base Case (기저 사례)

$T(k) \leq Ck$ for all $k \leq 100$

$\log_2(k) \leq Ck$가 성립하려면 $C \geq \dfrac{\log_2(k)}{k}$

$k \leq 100$일 때 $\dfrac{\log_2(100)}{100} \approx \dfrac{7}{100}$

⇒ $C \geq 7$이면 충분

Inductive Step (귀납 단계)

$T(k) \leq T(k/5) + T(7k/10) + dk$
귀납 가정 대입하면:

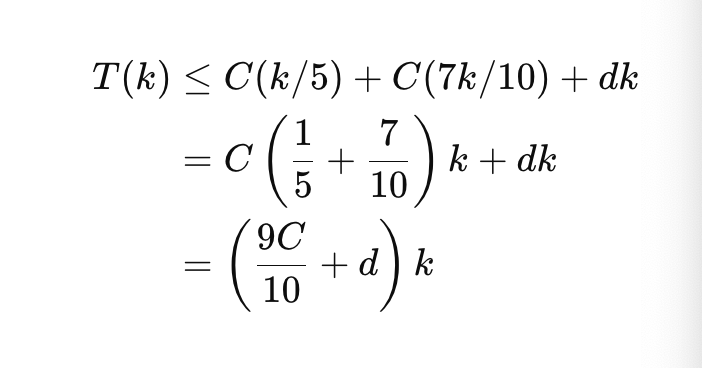
이게 $Ck$보다 작거나 같으려면:

$\dfrac{9C}{10} + d \leq C$

$\Rightarrow d \leq \dfrac{C}{10}$

$\Rightarrow C \geq 10d$

✅ 결론

따라서,
$C \geq \max{7,\ 10d}$ 일 때
모든 $n > 1$에 대해 $T(n) \leq Cn$이 성립하므로,
T(n)=O(n)

---