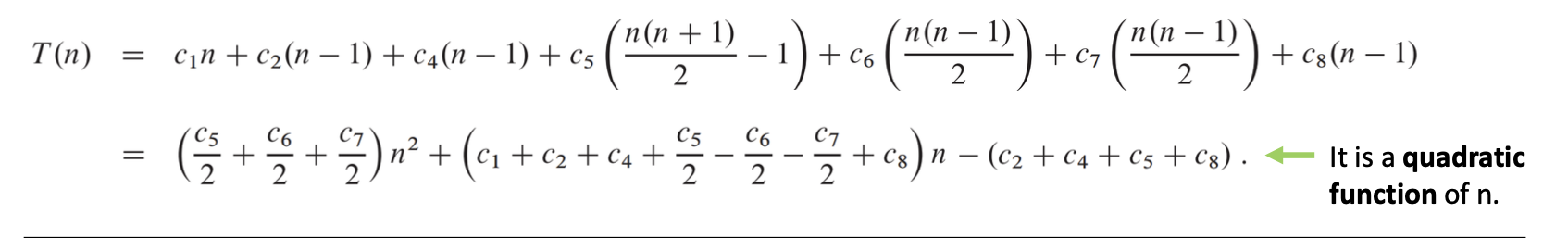시간 복잡도(Time Complexity)란?
시간 복잡도(Time Complexity)는 알고리즘이 입력 크기(𝑛)에 따라 수행하는 연산 횟수를 표현한 것이다.
즉, 입력 크기(n)가 커질 때 알고리즘의 실행 시간이 얼마나 증가하는지를 나타내는 척도라는 것!
삽입 정렬은 빠른가? (Is it fast?)

위 사진은 삽입정렬 의사코드를 분석한 사진이다
tⱼ 는 “j번째 반복(for 문에서 j값일 때)에 while 루프가 실제로 몇 번 실행되었는가?”를 의미한다. 즉, A[j]라는 원소를 이미 정렬된 부분에 삽입하려고 할 때, 얼마나 많은 비교 및 이동이 일어나는지 그 횟수(반복 수)를 세는 용도이다
만약 A[j]가 이미 올바른 위치에 있으면 while 루프가 한 번만 비교하고 끝나므로, tⱼ = 1이 될 수 있을 것이고, 반대로 A[j]가 정렬된 부분 리스트의 맨 앞으로 이동해야 한다면, while 루프가 여러 번 실행될 수 있고, 그러면 tⱼ 가 더 커짐(최대 j번 정도).
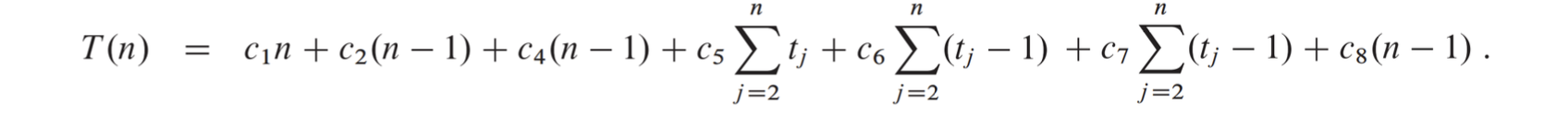
결과적으로, 삽입 정렬의 총 실행시간은 모든 cost x times 를 더한 값과 같다.
👍 Best case in insertion sort
삽입 정렬에서 가장 최선의 시나리오는 무슨 상황일까?
당연하게도, 이미 모든 배열이 정렬된 상태일 것이다.
모든 배열이 정렬된 상태에서 삽입정렬을 실시하면 어떻게 될까?
while ( i > 0 and A[i] > key ) 부분에서, A[i] > key가 바로 거짓이 될 것이다.
즉, j번째 삽입 시도에서 while 루프가 딱 1회(조건 확인)만 실행하고 끝난다는 의미이다
따라서
tⱼ= 1 (∀ j = 2, 3,…,n) 라는 결과가 나온다!
그 결과, 최종 식을 전개해보면 T(n)이 n에 비례하는 “선형 함수”로 나온다!
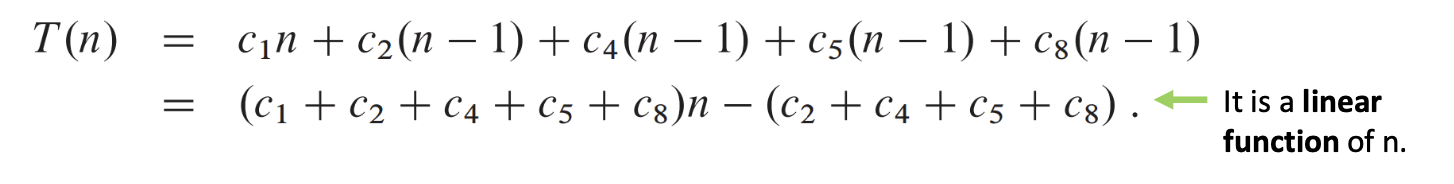
✅ 따라서 삽입정렬에서의 Best Case의 시간복잡도는 O(n)이 된다.
👎 Worst case in insertion sort
그렇다면 삽입 정렬에서 가장 최악의 시나리오는 모든 배열이 역순으로 정렬된 상태일 것이다.
모든 배열이 역순 정렬된 상태에서 삽입정렬을 실시하면 어떻게 될까?
삽입 정렬은 각 단계에서 새로운 원소가 이미 정렬된 구간의 맨 앞으로 이동해야 하므로, while 루프가 매번 (j-1)번쯤 실행된다.

그 결과, 최종 식을 전개해보면 결과적으로, 상수들을 무시하고 큰 항만 보면 n²에 비례하게 된다.