지금까지 우리는 알고리즘의 올바름(Correctness)에 대해 알아 보았다.
그 다음으로 중요한 효율성(Efficiency)에 대해 알아보자.
알고리즘의 효율성은 최대한 빠르게 동작하고, 최대한 적은 메모리를 사용해야한다는 특징이다.
즉, 시간 효율성(Time Efficiency)과 공간 효율성(Space/Memory Efficiency)이 중요하다는 것!
그 외에도 단순성, 일반성, 최적성, 등등이 있지만......넘어가도록하자.
우리는 갈 길이 멀다, 개가 짖어도 기차는 달려야하는 법이다.
점근 표기법(Asymptotic Notation)
우리가 런타임(runtime)을 측정할 때, 실제 시간은 환경에 크게 의존한다.
동일한 알고리즘이라도 내가 사용하는 컴퓨터의 하드웨어 성능, 프로그래밍 언어, 컴파일러 최적화에 따라 실행 시간이 달라진다는 것이다.
하지만 우리는 이러한 알고리즘 외적인 요소들을 초점에 두고자 이 강의를 배우는 것이 아니다.
그렇기에 우리는 세부사항을 전부 배제하고, 보편적이고 일반화된 척도를 사용해 알고리즘의 성능을 평가한다.
그러기 위해서 우리는 바로 점근 표기법을 사용할 것이다.
점근 표기법(Asymptotic Notation)이란 입력 크기 n이 매우 커질 때, 알고리즘의 실행 시간이 어떻게 증가하는지를 수학적으로 단순화하여 나타내는 방법을 의미한다.
한마디로 그냥 n을 엄~청나게 늘려서 어떻게 되는지 한번 보자 라는 마인드로 이해하면 될 것이다.
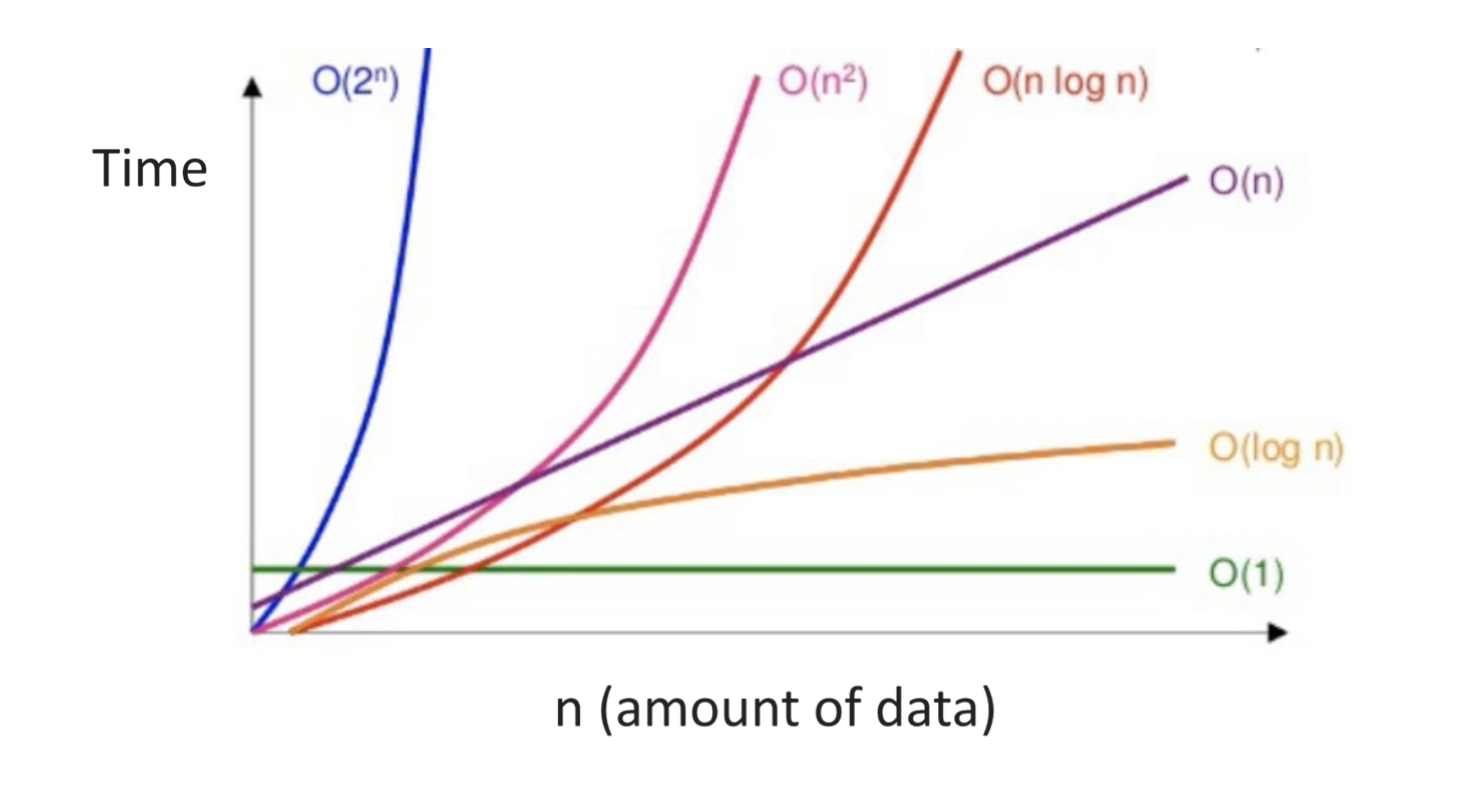
1. 키 인사이트(Key insight)
- 알고리즘의 ‘실행 시간이 입력 크기 n에 따라 어떻게 증가하는가’를 중점적으로 본다.
- “한 알고리즘이 다른 알고리즘보다 ‘더 빠르다’”는 것은, 같은 크기의 입력이 주어졌을 때 실행 시간이 더 천천히 증가한다는 의미.
2. 장점 (Pros)
- 외적인 요소들을 무시하고 순수한 알고리즘 복잡도만 비교할 수 있음.
- 알고리즘 분석이 훨씬 간단해짐 (tractable)
3. 단점 (Cons)
- 입력 크기 n이 충분히 커야 의미가 있다
- 상수 계수나 작은 항을 무시함으로써 나타나는 착시
Big-O (빅오) : 최악의 경우 시간 복잡도를 나타내는 표기법
“어떤 함수를 상한선으로 표현”
예: T(n) = O(n²) 은 “알고리즘 실행 시간이 n² 이내로 제한된다”라는 의미
Big-Ω (빅오메가) : 최선의 경우 시간 복잡도를 나타내는 표기법
“어떤 함수를 하한선으로 표현”
예: T(n)=Ω(n) 는 “알고리즘 실행 시간이 최소한 n에 비례한다”는 의미
Big-Θ (빅세타)
상하한이 같은 경우, 즉 최악과 최선이 같은 차수일 때
예: T(n)=Θ(nlogn) 은 “알고리즘 실행 시간이 n log n에 정확히 비례한다”는 의미
즉, 점근 표기법은 큰 입력(n → 무한대)을 다룰 때,
가장 높은 차수 항만 남겨서 알고리즘의 성능을 간결하게 표현해 주는 수학적 도구이다!
Big-O Notation
1. 문제 상황 / 전제조건
- T(n), g(n)은 모두 양의 정수에 대한 증가 함수(positive, increasing functions)라고 가정.
- T(n): 보통 알고리즘의 실행 시간(또는 복잡도)라 생각할 수 있음.
- g(n): 비교 대상이 되는 “성장 함수”.
2. 정의
- g(n)의 증가속도가 최소 T(n)만큼, 혹은 더 빠르다면 T(n) is O(g(n))이라고 한다
→ 즉, 입력이 충분히 커졌을 때, T(n)이 g(n)의 배수 이상으로 커지지 않는다는 의미.

c: T(n)을 덮기 위해 g(n)에 얼마만큼을 곱해야 하는지 나타내는 척도
n₀: “어느 시점 이후”부터는 “T(n) ≤ c×g(n)”을 항상 보장한다는 경계
∃: “~인 값(또는 요소)가 하나 이상 존재한다.”
∀: “~인 값(또는 요소) 모두에 대해 조건이 참이다.”
s.t : " ~을 만족하면서”, “~라는 조건하에”
어떤 상수 c>0 와 임의의 기준 n₀ > 0 을 잡으면, 그 뒤로 모든 n ≥ n₀ 에 대해 T(n) ≤ c⋅g(n)을 만족한다는 조건이다.
3. 해석
- 쉽게 말해서, 입력(n)이 충분히 클 때, T(n)이 c x g(n)을 넘어서지 않는다라는 의미이다
- 즉, T(n)이 아무리 염병을 떨어도 최대 ~g(n) 정도로 커진다는 상한선(upper Bound)를 제공한다는 것
그 말은 T(n)이 g(n)보다 더 빠르게 증가하지 않는다는 뜻이므로, 알고리즘의 시간 복잡도가 ≤ O(g(n)) 범위 안에 있음을 보장해준다는 것이다.
예시.
- T(n) = 5n + 10 은 O(n)
- 큰 n에서 5n + 10 ≤ 15n (예, c= 15, n₀ = 10 등 설정 가능)
- T(n) = 2n² + 3n 은 O(n²)
- 큰 n에서 2n² + 3n 은 ≤ 5n² (예, c= 5, n₀ = 3 등 설정 가능)
Big-O 표기법 증명 방법
이제 빅오 표기법이 무엇인지 알게 되었으니, 증명법에 대해 알아보자.
1. T(n) = O(g(n))를 증명하는 방법
핵심은 “T(n)과 g(n)이 주어졌을 때, 어떤 양의 상수 c와 기준점 n₀가 존재해서,
n이 n₀ 이상이면 T(n) ≤ c·g(n)을 만족한다” 는 사실을 직접 보여주면 된다.
즉, 빅오 표기법을 만족하는 c와 n₀을 하나라도 찾아서 보이면 된다는 것.
예시: T(n)=n, g(n)=n log₂n
주장: n = O(n log₂n)
증명 방법:
1. c와 n₀를 찾아라. 여기서는 c=1, n₀=2 로 선택한다.
2. 이제, n ≥ n₀(즉, n≥2)이면 n ≤ 1 × n log₂n 이 성립함을 보이면 됨.
3. n ≥2이면 log₂n ≥1 이므로, n log₂n ≥ n×1 = n.
4. 따라서 n ≤ n log₂n. 즉, “n ≤ c·(n log₂n) = n log₂n”이 참.
✅ 따라서 T(n)=n은 O(n log₂n)이 맞다.
2. T(n) ≠ O(g(n))를 증명하는 방법
핵심은 “T(n)이 g(n)에 의해 상한(덮이지)되지 않는다”는 걸 보이려면,
‘T(n)=O(g(n))라 가정했을 때 모순(contradiction)이 일어남’을 보여주면 된다.
예시: T(n)=n², g(n)=n
증명 (모순법):
1. 가정: n² = O(n)라고 해보자.
⇒ 상수 c>0, n₀>0가 있어서, n≥n₀이면 항상 n² ≤ c·n.
2. 반례를 찾아라:
- n을 max{c, n₀} + 1로 두면, n은 c보다 크고 n₀보다도 큼.
- 이때 n²와 c·n을 비교:
n² = n·n > n·c (왜냐하면 n>c)
⇒ n² > c·n.
-> 즉, n² ≤ c·n을 깨뜨리는 n을 만들 수 있음.
3. 결론: 가정이 모순을 일으킴 ⇒ n² ≠ O(n)
Big-Ω Notation
Big-Ω는 함수의 성장률에 대한 "하한선(Lower-Bound)"을 나타내는 표기법이다.
즉, "실행 시간(T(n))이 적어도 g(n) 이상으로 빠르게 증가한다”는 것을 의미한다.
예: T(n) = Ω(n)
→ “T(n)은 적어도 n에 비례해서 증가한다.”
→ “T(n)은 최소 이 정도로는(n) 커진다.”
예시
- T(n) = 5n + 10
상수나 낮은 차수 항을 무시하면, n만큼 증가.
따라서 T(n)=Ω(n) 라고 말할 수 있음.
실제 증명은 “5n+10 ≥ c·n (for some c>0, n≥n₀)”를 보이면 됨.
예: c=5, n₀=2 (사실 모든 범위의 n₀가 포함된다)
T(n)=n log n
분명히 n보다 빠르게 증가하지만, n²보다는 느린 증가.
Ω(n)일 수도 있고, Ω(n log n)도 됨.
더 구체적으론 n log n = Ω(n), 그리고 n log n = Ω(n log n) (정확한 하한).
Big-Θ(Theta) Notation

위로는 c₂·g(n)이 ‘T(n)을 충분히 덮는다(상한)’
아래로는 c₁·g(n)이 ‘T(n)보다 작지 않다(하한)’
⇒ T(n)이 g(n)과 같은 차수로 성장한다고 볼 수 있음.
Big-Θ: “T(n)은 g(n) 이하로도, g(n) 미만으로도 치우치지 않는다.”
T(n)=5n+10, g(n)=n
상한: T(n)=O(n)
하한: T(n)=Ω(n)
따라서 T(n)=Θ(n).
예제 함수 T(n)
- T(n) = 3n + 10
1) Big-O:
- 3n + 10 = O(n) (Ex, c=4, n₀=10)
2) Big-Ω:
- 3n + 10 = Ω(n) (Ex, c=2, n₀=5)
3) Big-Θ:
- 결국 3n + 10은 O(n)이면서 Ω(n)이므로
3n + 10 = Θ(n)
