Master Method

Master Method

모든 부분 문제(sub-problem)의 크기가 같은 경우에
점화식을 풀 수 있는 공식(formula)을 제공함.

다음과 같은 꼴의 점화식에서만 적용 가능함:

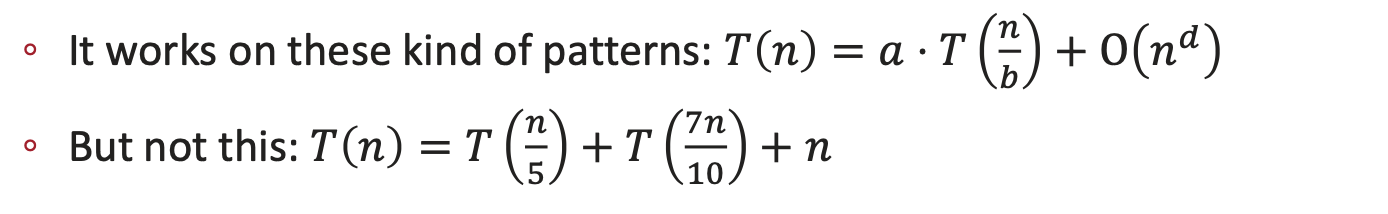
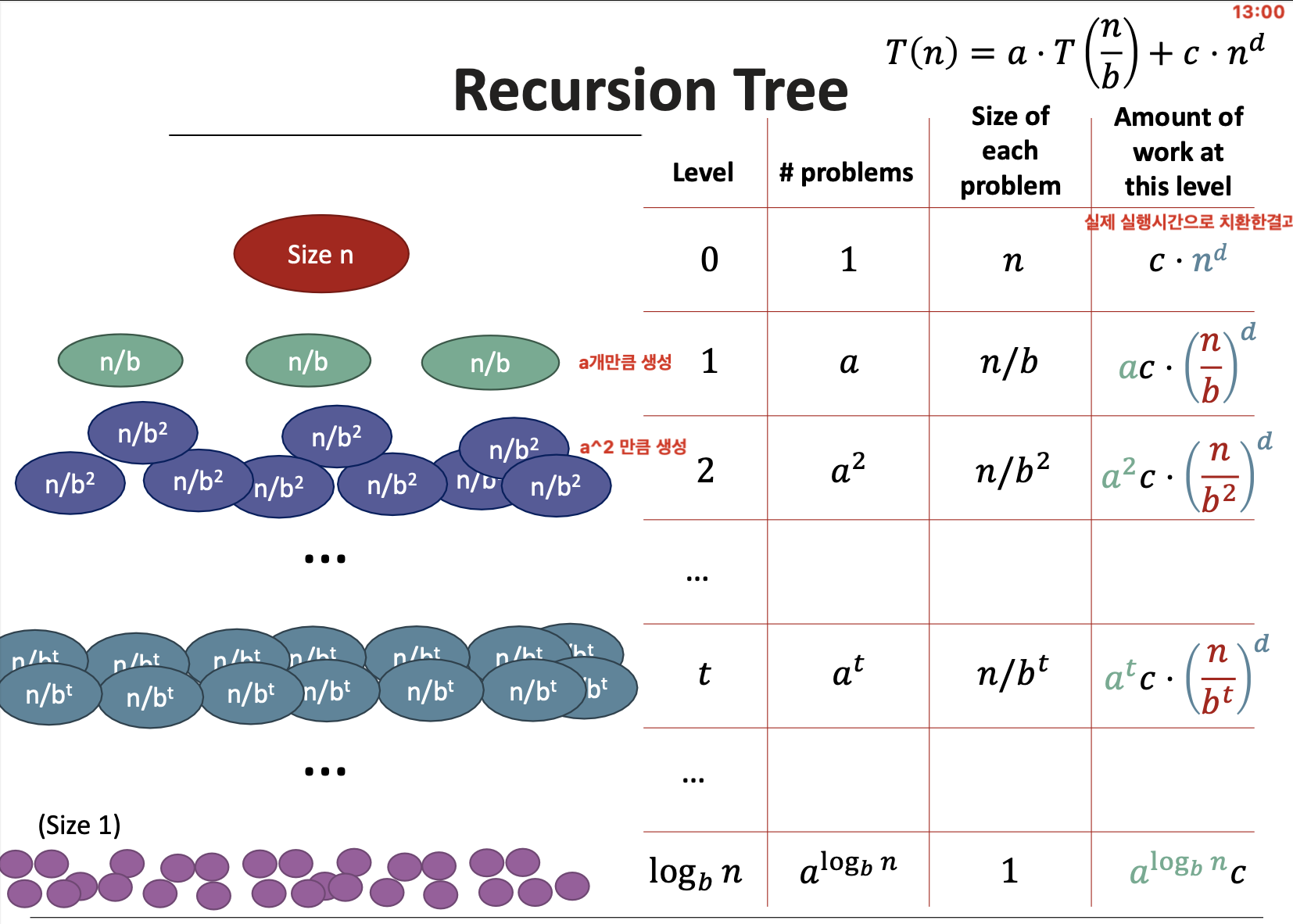
a = 쪼갠 부분 문제(subproblems)의 개수

n/b = 부분 문제의 크기

O(nᵈ) = 나누고 병합할 때 드는 비재귀적 작업량 (combine)

즉 부분 문제가 같은 크기로 쪼개질 때만 사용 가능하다는 것!

마스터 정리 기본형태

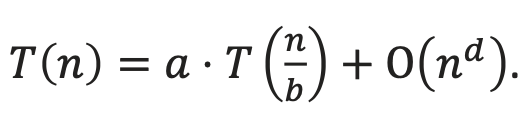
어떤 점화식이 다음 형태로 표현될 때 ( 𝑎 ≥ 1, 𝑏 > 1, 𝑑는 모두 상수 (입력 n과 무관)
그 점화식의 해(시간 복잡도)는 다음 3가지 케이스 중 하나로 결정된다.

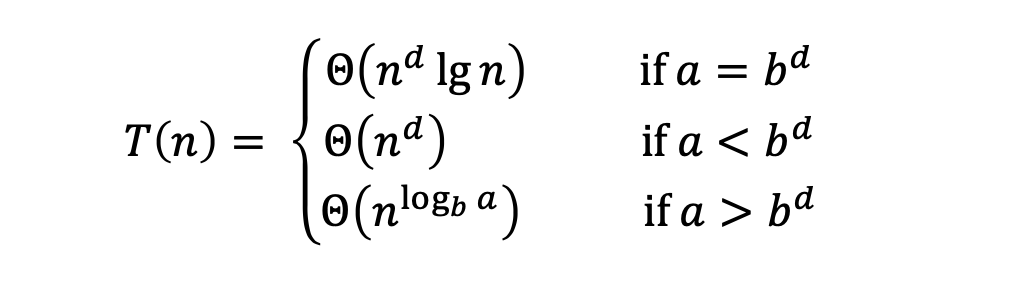
Merge Sort 적용 예시

병합 정렬의 점화식은 다음과 같다

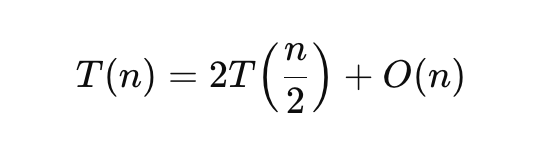
이를 마스터 정리에 대입하면,
a: 문제를 쪼갰을 때 만들어지는 하위 문제의 개수이다

• 머지 정렬에서는 a=2 (두개의 절반 배열)

b: 문제 크기가 얼마나 줄어드는지 나타냄

• 머지 정렬에서는 b=2 (절반으로 줄이니까)

d: 하위 문제 외에 발생하는 작업량이 nᵈ 정도라고 보는 것

• 머지 정렬에서 병합에 걸리는 시간이 O(n) → 즉 d=1

a= bᵈ= 2 이므로 케이스 1에 해당된다.

따라서 병합 정렬의 최악의 시간복잡도는 Θ(nlogn)이 되는 것이다.

---

이렇게만 보면 잘 와닿지않는다.
비유를 통해 제대로 한번 이해해보자

💁🏻 a : 부하 직원 수 (하청 개수)

당신은 한 직장의 상사이다.
업무 하나가 들어오면, 혼자 다 하지 않고 하청에 짬을 때린다.
하나의 업무를 a명의 직원에게 나눠준다면, 각 직원이 이 일을 또 나눠서 처리할 것이다.

예시:

• 업무를 2명에게 나눠주면 → a=2
• 업무를 3명에게 나눠주면 → a=3

즉, a는 "몇 개의 하위 문제로 쪼개는가"에 해당된다.

📦 b : 각 부하에게 주는 일의 크기 (작업 분할 비율)

각 부하 직원에게는 전체 일의 몇 분의 1 정도를 맡길것인가?

예시:

• 전체가 100이라면, 50(절반)씩 나눠주면 → b=2
• 100을 3명에게 33(1/3)씩 나눠주면 → b=3

즉, b는 "각 하위 문제의 크기"를 의미한다.

🔧 d : 직접 처리하는 업무량 (회사의 overhead)

양심적으로 하청을 줘도, 하청 주기 전에 문서 정리나 준비 작업은 내가 해야할것이다.
즉, Θ(bᵈ)은 하청을 주기 전에 본사에서 처리하는 일의 양이다.

이는 하나의 재귀 호출에서 하위 문제 외에 수행하는 추가 작업의 시간 복잡도를 나타낸다
분할, 병합, 정렬, 비교 등의 작업이 여기에 포함된다(할배잡 st)

예시:

• 내가 정리만 살짝 하면 → d=1 (linear)
• 큰 정리나 비교가 많으면 → d=2 (quadratic)

---

Recursion Tree

---

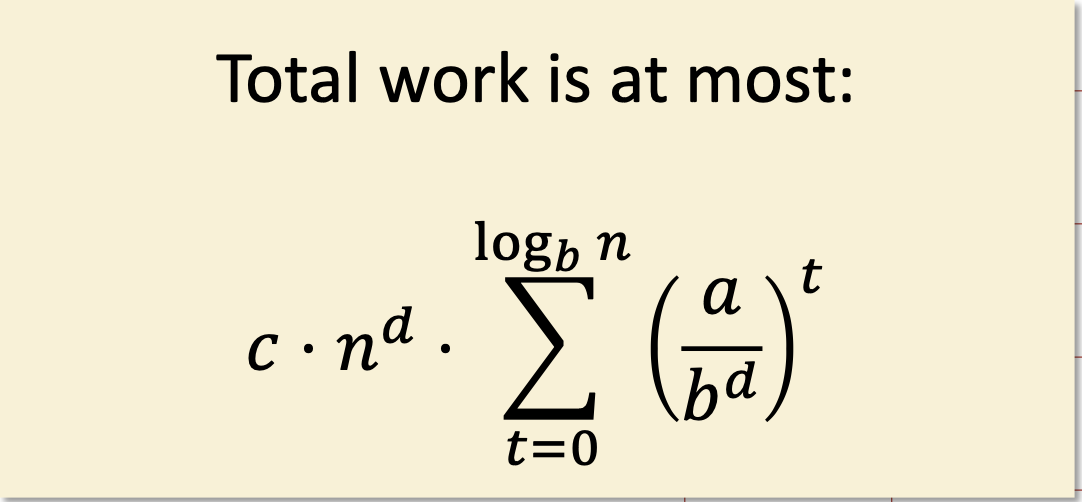
Case별 Recursion Tree

우리는 Master 정리에 대해서 끊임없는 싸움을 계속합니다.

a는 서브문제의 개수를 의미한다.
bᵈ는

🔴 왼쪽: a < bᵈ

"Branching causes the number of problems to explode!"
→ 문제를 분할할수록 하위 재귀 호출의 갯수가 기하급수적으로 늘어난다!


"The most work is at the bottom of the tree!"
→ 각 문제는 작지만, leaf 쪽에 너무 많은 문제들이 몰려 있어서, 전체 시간의 대부분은 하단에서 발생한다.

→ 상위 레벨은 몇 개 없고, 하위 레벨에서 많은 일들이 터져나오는 상황.
→ 전체 작업량은 leaf에서 터짐 → Θ(nᵈ)

🟢 오른쪽: a > bᵈ

"The problems lower in the tree are smaller!"
→ 재귀를 내려갈수록 문제는 작아지지만

"The most work is at the top of the tree!"
→ 반대로, 재귀의 상단에서 큰 크기의 문제들이 적지만 큰 작업을 하게 되는 경우

→ 재귀는 많지만, 결국 상단에서의 큰 작업이 주도권을 쥠
→ 전체 작업량은 상단이 책임 → Θ($n^{\log_b a}$)

---

Tall and Skinny Tree

위와 같은 예제가 있다고 가정하자.
$a = 1,\ b = 2,\ d = 1$ 이다.

우리가 확인해야 할 관계는 $a \ <\ b^d$, 즉
$1 < 2^1 = 2$, 만족하므로 → Case 2를 적용한다

📌 Master Theorem 적용

If $a < b^d$,
then $T(n) = \Theta(n^d) = \Theta(n)$

✅ 결론

작업량의 대부분은 트리의 최상단(Top) 에서 발생한다.
즉, 루트 노드에서의 일이 전체 수행 시간에 가장 큰 영향을 미친다.

따라서, $T(n) = \Theta(n)$

---

Bushy Tree

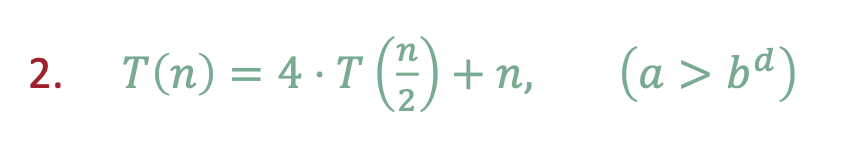
위와 같은 예제가 있다고 가정하자.
$a = 4,\ b = 2,\ d = 1$ 이다.

우리가 확인해야 할 관계는 $a > b^d$ , 즉
$4 >2^1$, 만족하므로 → Case 3을 적용한다

📌 Master Theorem 적용

If $a > b^d$,
then $T(n) = \Theta(n^{\log_b a})$

여기선 $\log_2 4 = 2$
→ $T(n) = \Theta(n^2)$

✅ 결론

문제를 쪼갤수록 하위 문제 수가 기하급수적으로 증가한다.
각 하위 문제는 작지만, 개수가 많아서 leaf에서 하는 작업량이 전체 시간 복잡도를 지배한다

따라서, $T(n) = \Theta(n^2)$

---

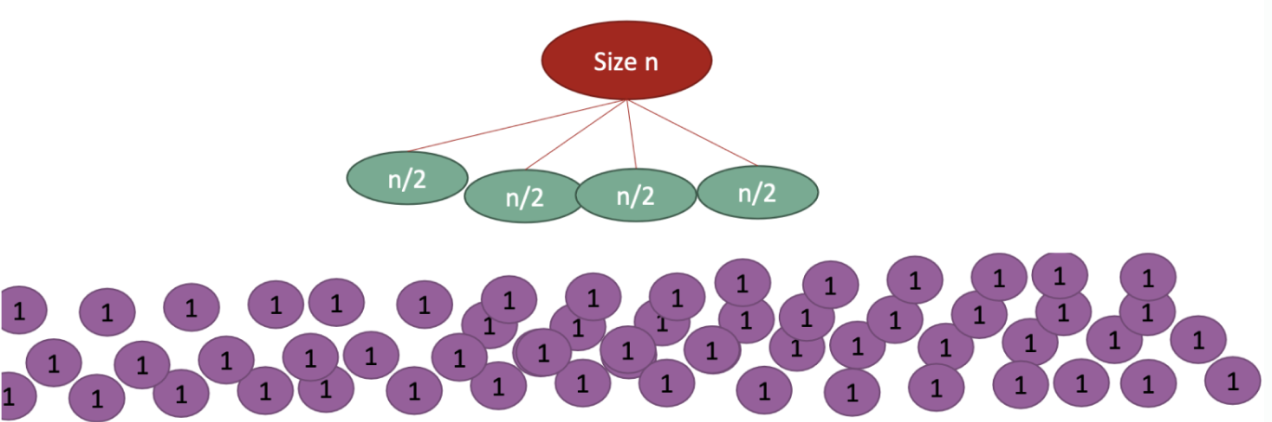
Just Right

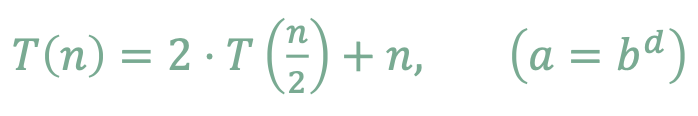
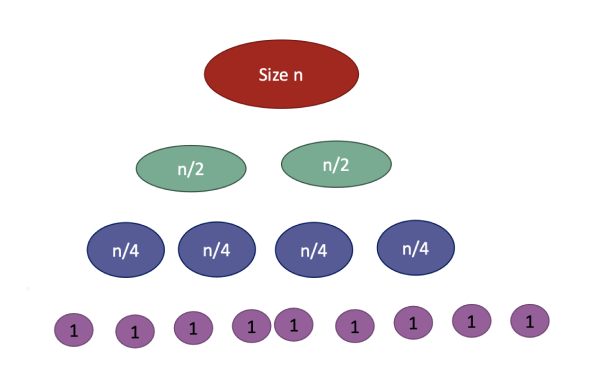
위와 같은 예제가 있다고 가정하자.
$a = 2,\ b = 2,\ d = 1$ 이다.

우리가 확인해야 할 관계는 $a = b^d$ , 즉
$a = b^d$, 만족하므로 → Case 1을 적용한다

📌 Master Theorem 적용

If $a = b^d$,
then $T(n) = \Theta(n^d \log n)$

여기선 $d = 1$
→ $T(n) = \Theta(n \log n)$

✅ 결론

각 레벨마다 작업량이 동일하다.
(위에도 Θ(n), 아래도 Θ(n), 중간도 마찬가지)

전체 시간복잡도는
(레벨 수) × (레벨당 작업량)
→ $\log n \cdot \Theta(n) = \Theta(n \log n)$

---

Substitution Method

이번엔 재귀점화식을 푸는 마지막 방법, Substitution Method에 대해 알아보자
이번 챕터 양 개많은거 안다, 미안하다.
하지만 이게 마지막이니 함 달려보자

🧠 Substitution(치환) Method란?

재귀 점화식을 푸는 또 하나의 방법으로, Master Method보다 더 일반적인 방법이다.
즉, Master Method가 적용되지 않는 상황에서도 쓸 수 있습니다(다만 수학적 센스가 좀 필요하다)

과정을 요약하자면 다음과 같다.

✅ Step 1 : 정답일 것 같은 추정식을 만든다
예: 점화식이 T(n) = 2T(n/2) + n이라면,
"아마도 정답은 $\Theta(n \log n)$일 것이다" 라고 예상.

✅ Step 2 : 수학적 귀납법 등으로 그 추정식을 증명한다.
즉, T(n) ≤ cn log n 같은 걸 귀납적으로 보여서 정말로 그게 상한/하한임을 입증하는 것.

✅ Step 3 : Profit 😎
→ 증명에 성공하면 이게 진짜 정답이란 것을 알 수 있다

이제, 방금 설명한 예제를 조금 더 자세히 증명해보자

---

Step 1 : Guess the Answer

✅ 점화식 전개 (Unrolling the recursion)

계속해서 T(n)을 확장하며 패턴을 관찰한다

🔄 점화식 전개 (Unrolling)

$T(n) = 2 \cdot T\left(\frac{n}{2}\right) + n$
$= 2 \cdot \left(2 \cdot T\left(\frac{n}{4}\right) + \frac{n}{2}\right) + n$
$= 4 \cdot T\left(\frac{n}{4}\right) + 2n$
$= 4 \cdot \left(2 \cdot T\left(\frac{n}{8}\right) + \frac{n}{4}\right) + 2n$
$= 8 \cdot T\left(\frac{n}{8}\right) + 3n$
...

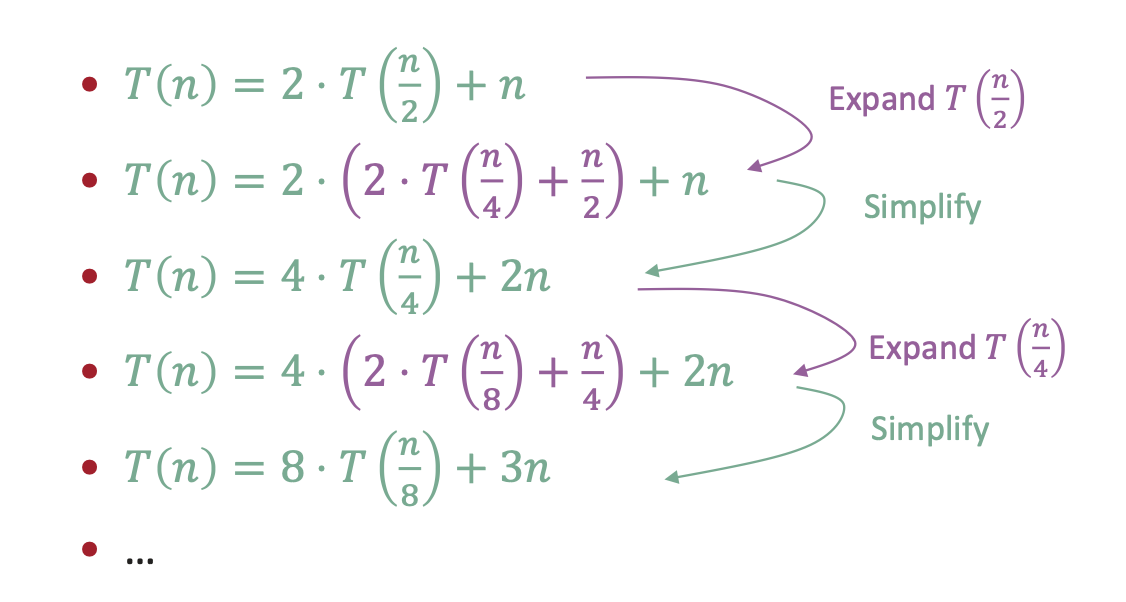
이런 식으로 전개를 계속하면 패턴을 찾을 수 있다.

📐 패턴 추측

$T(n) = 2^t \cdot T\left(\frac{n}{2^t}\right) + t \cdot n$
이제 우리는 마지막까지 전개해보며 추정식을 만들어낼 수 있다.

⛳ base case 대입

$2^t = n$ 일때, $t = \log n$
$T(n) = n \cdot T(1) + n \cdot \log n = n + n \log n = n \ ( \log n + 1)$

---

Step 2: Prove the Guess is Correct

Inductive Hypothesis: $T(n) = n(\log n + 1)$

Base Case ($n = 1$): $T(1) = 1 \cdot (\log 1 + 1) = 1$

Inductive Step:

가정 : (Inductive Hypothesis for $1 \le n < k$)

$T(n) = n(\log n + 1)$ for all $1 \le n < k$

증명 (for $n = k$):

$T(k) = 2 \cdot T\left(\frac{k}{2}\right) + k$ (정의에 의해)

$= 2 \cdot \left(\frac{k}{2}(\log \frac{k}{2} + 1)\right) + k$ (귀납 가정 대입)

$= k(\log \frac{k}{2} + 1) + k$

$= k(\log k - \log 2 + 1) + k$

$= k(\log k - 1 + 1) + k$

$= k(\log k) + k$

$= k(\log k + 1)$

따라서 귀납 가정은 $n = k$ 에 대해서도 성립함.

✅ 결론

모든 $n \ge 1$에 대해
$T(n) = n(\log n + 1)$이 성립함.
즉, 최종적으로 $T(n) = \Theta(n \log n)$.

---

Step 3: Profit

✅ 정리된 귀납법 수식들
귀납 가정: $T(n) = n(\log n + 1)$

기본 단계: $T(1) = 1 = 1 \cdot (\log 1 + 1) = 1$

귀납 단계 시작: $T(k) = 2 \cdot T\left(\frac{k}{2}\right) + k$

귀납 가정을 대입: $T\left(\frac{k}{2}\right) = \frac{k}{2} \cdot \left(\log \frac{k}{2} + 1\right)$

최종 결론: $\forall n \ge 1, \quad T(n) = n(\log n + 1)$

➡️ $\Theta(n \log n)$ 로 수렴