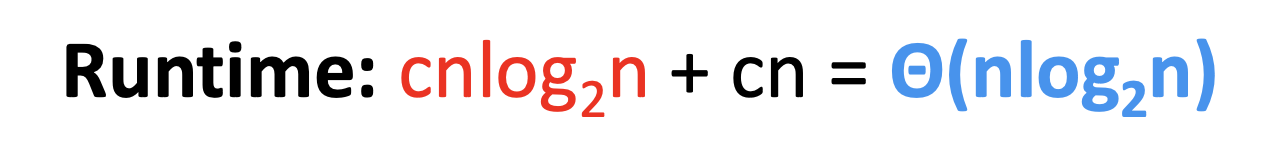분할 정복 시간복잡도
분할 정복 알고리즘의 런타임을 분석하기 위해선 점화식을 사용해야한다
그렇다면 점화식이란 무엇일까?
1️⃣ 점화식(Recurrence Relation)이란?
점화식이란 어떤 수열에서 특정 항을 이전 항(또는 여러 개의 이전 항)과의 관계로 정의하는 식을 의미한다.
즉, 이전 값(또는 몇 개의 이전 값들)과의 연산을 통해 다음 값을 계산할 수 있도록 표현된 수식을 말합니다.
점화(漸化)라는 한자어를 풀어보자면 "점진적으로 변화함"을 의미한다.
그리고 분할 정복법에서 문제 크기가 n일 때, 총 수행 시간 T(n)은 다음과 같이 정의된다
(T(n)은 크기 n짜리 문제를 푸는 전체 실행 시간(런타임)을 의미한다)
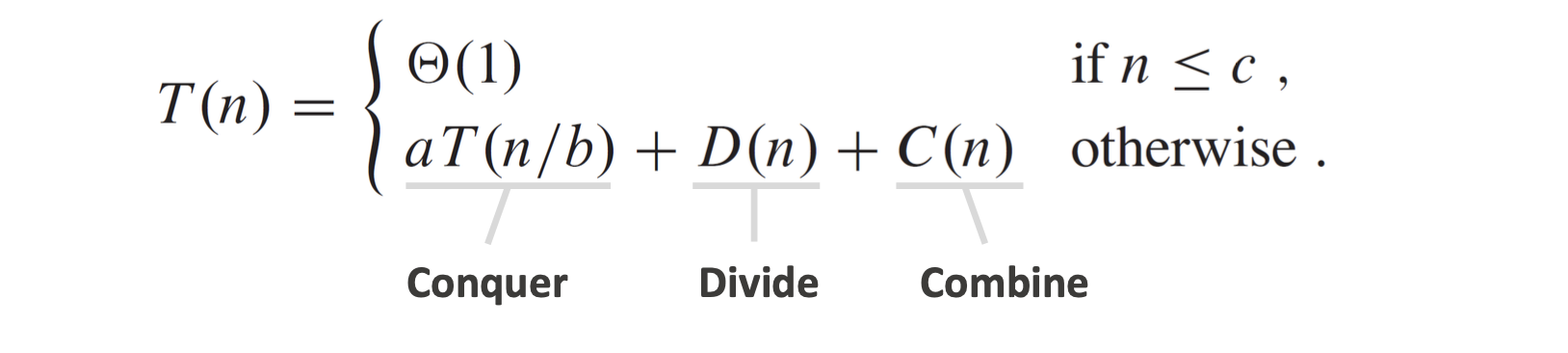
각 항목의 의미
aT(n/b) : 전체 문제를 크기 n/b인 하위 문제 a개로 나눠서 정복(Conquer)
D(n) : 문제를 나누는 시간 (Divide)
C(n) : 나눈 결과를 합치는 시간 (Combine) (Merge과정)
즉, 전체 시간은 위 세 단계의 시간의 합이 된다.
Divide 수행시간

우선 가장 간단한 Divide 단계부터 알아보자.
Divide는 말그대로 배열을 반으로 나누는 작업이다.
즉, 중간 인덱스 q = ⌊(p + r)/2⌋를 계산하는 부분을 의미!
이 연산은 덧셈, 나눗셈, 버림(floor) 연산 한 번이면 끝이난다.
즉, 배열의 크기 n에 상관없이 항상 같은 시간 안에 실행된다
➡️ 그래서 이 단계의 시간 복잡도는 Θ(1) (상수 시간)이다.
🙋♂️ :왜 T(1)이 아닌 Θ(1)로 사용하나요?
🙆♂️ : T()는 시간의 실제 값, Θ()는 시간의 성장 속도을 의미한다. 알고리즘 분석에서는 정확한 시간보다 "얼마나 커지냐" 가 핵심이기 때문에, 입력의 크기와 관계 없이 걸리는 시간이 일정한 성장속도임을 표현하기위해 Θ(1) 으로 사용한다~
Conquer 수행시간
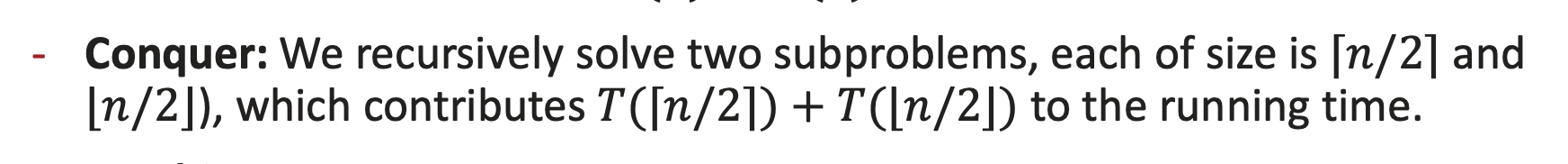
우리는 두 개의 부분 문제를 재귀적으로 해결한다.
각 부분 문제의 크기는 ⌈n/2⌉ (올림)과 ⌊n/2⌋ (내림) 이고,
이 두 문제를 푸는 데 드는 전체 시간은 T(⌈n/2⌉) + T(⌊n/2⌋) 만큼 기여한다.
또 머리가 아파지기 시작하지만 그럴 이유가 전혀 없다!
다시 한번 상기해보자, T(n)이 가지는 의미는 무엇인가?
➡️ T(n)은 크기 n짜리 문제를 푸는 전체 실행 시간을 의미한다.
그렇다면 전체 배열의 크기가 n이라면, 그것의 전체 정렬시간은 얼마일까?
너무나도 당연하게 T(n)이 될것이다.
자, 그럼 여기에 분할 정복의 성질을 추가해보는 것이다.
분할 정복의 정복(Conquer)과정에선 배열을 반으로 나눠서 각각 정렬한다
그럼 두개로 나뉜 배열의 크기는?
⌈n/2⌉ (올림)과 ⌊n/2⌋ (내림)이 되는 것이다!
그럼 각각의 정렬시간은?
ㅆ바것 볼것도 없지
T(⌈n/2⌉) + T(⌊n/2⌋) 이 되는 것이다.
✅ 한마디로 현재 문제 크기 n을 두 조각으로 나눠서 각각 정렬하는데 걸리는 시간을 의미히는거시다~
Combine 수행시간
Combine, 즉 Merge 단계에서의 수행시간을 얼마나 걸릴까?
이미 정렬된 두 배열을 하나로 합치려면 어떤 작업이 필요할까?
각 원소를 한 번씩만 보면서 비교하며 진행하면 될 것이다.
예를 들어 L에 3개, R에 3개 → 총 6개의 원소를 한 번씩만 살펴보면 정렬 가능하며
그리고 A라는 배열에 차례대로 넣기만 하면 됨.
즉, 배열 A의 길이가 n이라면,L과 R을 합치기 위해선 최대 n번의 비교와 복사가 필요하다
→ 즉, MERGE 과정은 입력 크기에 비례해서 걸리는 시간 = Θ(n)
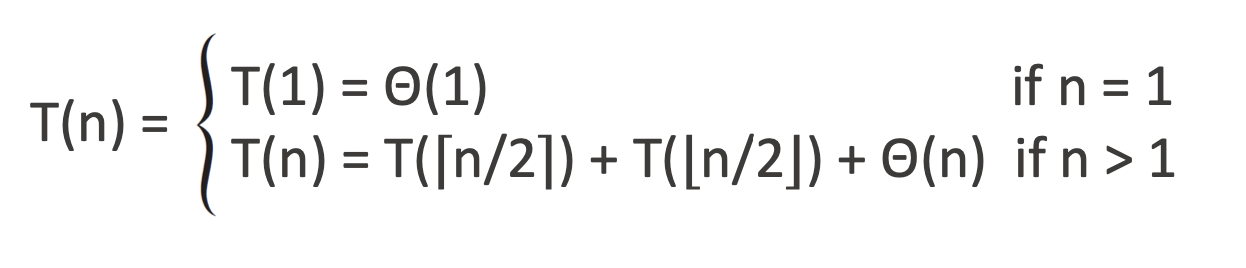
지금까지 배운 내용들을 토대로 Merge Sort의 점화식을 수학적으로 나타낸 것이다
그러나 점화식으로 표현한 T(n)은 별로 유용하지 않다.
🤔 왜?
점화식은 T(n)이 계속 자기 자신을 재귀적으로 호출하는 방식이기 때문에
→ 실제 T(n)의 전체적인 시간 복잡도가 얼마인지 직관적으로 보기 힘들다
그래서 우린 점화식을 closed-form expression으로 바꿀것이다
closed-form은 복잡한 재귀나 반복 없이 표준 연산만으로 표현한 완성된 식을 의미한다.
Simplication!
이제우리는 위에서 보였던 점화식을 단순화해볼 것이다.
🔥 Simplification 1

➡️ Big-Θ 정의를 활용해 Θ(1)과 Θ(n)을 부등식으로 바꾸자!
🔁 왜 부등식으로 바꿀까?
Big-Θ(세타)는 어떤 함수 f(n)이 Θ(g(n))이면, 결국 "c₁·g(n) ≤ f(n) ≤ c₂·g(n)"이 충분히 큰 n₀ 이상에서 항상 성립함을 의미한다
즉, Θ는 어떤 범위 안에 갇혀 있다는 것이지, 딱 정확하게 그 값이다! 라는 뜻은 아니다.
그래서 실제 계산할 땐 상한선만 보는 부등식 형태로 바꿔서 점화식을 다룹니다.
🔥 Simplification 2
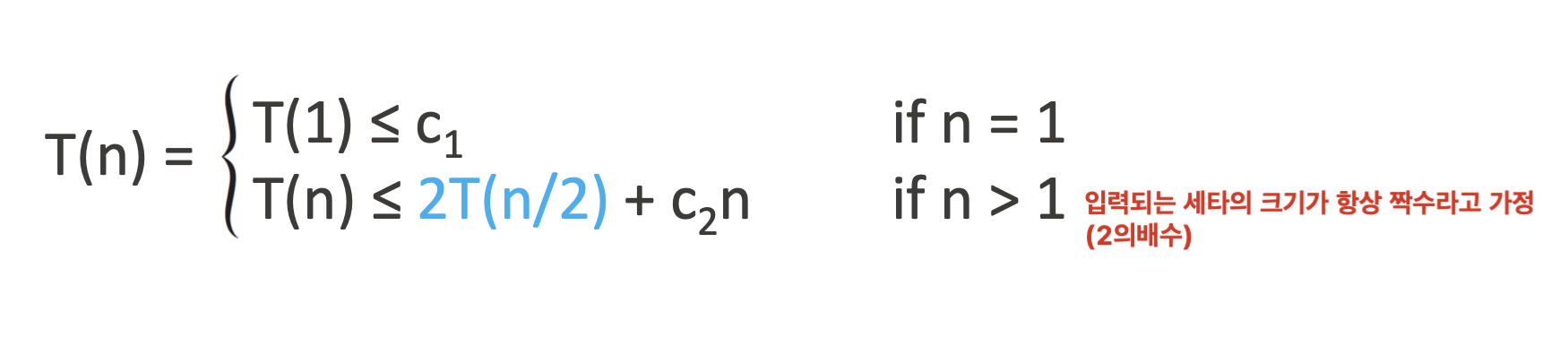
➡️ n이 2의 거듭제곱이라고 가정하자 (ex: 1, 2, 4, 8, 16...)
🧠 왜 이렇게 가정하냐면?
복잡한 점화식을 수학적으로 쉽게 풀기 위해서예요.
n을 2의 거듭제곱으로 정하면 ⌊n/2⌋, ⌈n/2⌉ 모두 정확히 n/2가 돼서 계산이 단순해집니다.
즉, T(⌈n/2⌉) + T(⌊n/2⌋) → 그냥 2T(n/2)로 깔끔하게!
🔥 Simplification 3
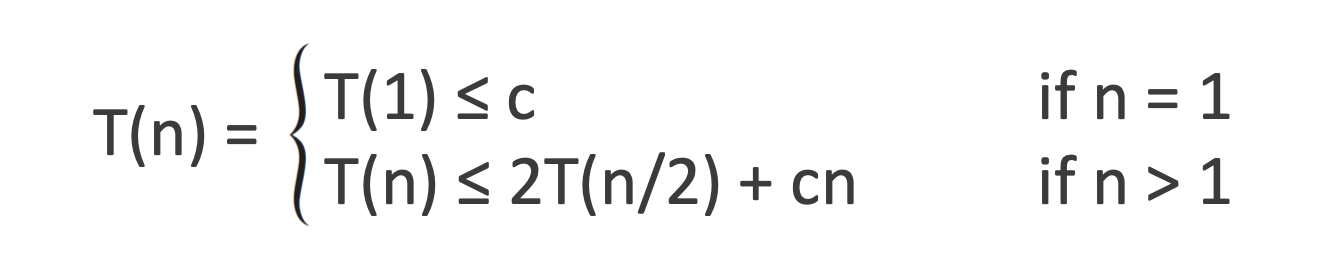
➡️ 앞에서 등장한 두 상수 c₁, c₂ 중 더 큰 값을 c라고 정하자
🧠 왜 이렇게 하냐면?
어차피 우리는 상한(upper bound) 을 구하는 중이기 때문에,
두 값 중 더 큰 걸로 통일해서 계산하면 항상 넉넉하게 잡히는 안전한 추정이 됨.
이제 드디어! 마참내!
정복 단계: 2T(n/2) 과 결합(combine): c·n으로 깔끔하게 정리되었다.
이걸 재귀 트리 방식으로 풀면 전체 시간복잡도를 계산할 수 있다.
Solving Recurrences
점화식(재귀 관계식)을 푸는 데엔 다양한 방법들을 사용할 수 있다.
뭐가 됐든, T(n)이라는 점화식을 사람이 이해하기 쉬운 closed-form으로 바꾸는 것이 목적!

그리고 우리는 위 세가지 방법을 사용해볼 것이다.
세가지 방법을 요약하자면
1. 🧮 Recursion Tree Method (재귀 트리 방법)
-
점화식을 트리 구조로 시각화함.
-
각 레벨의 비용을 계산하고 전체 합을 구함
-
비유: 나무 한 그루를 그리고 그 가지마다 비용이 얼마나 드는지 다 합쳐보는 방식.
-
👉 직관적이고 시각적이지만, 수식화가 길어질 수 있음.
2. 🧠 Master Method (마스터 방법)
-
정해진 형태의 점화식일 때 한 방에 결과를 뽑을 수 있음
-
a, b, f(n) 조건을 보고 바로 Θ(…) 결과를 뽑아내는 공식처럼 외우는 방법
-
👉 빠르고 편하지만, 형식이 맞아야 사용 가능
3. 🧪 Substitution Method (대입 방법)
-
수학적인 귀납법처럼, 가정하고 증명하는 방식
-
예: “T(n) ≤ cnlogn”이라고 가정하고, 그게 성립하는지 증명함
-
👉 가장 엄밀한 방식이지만, 직접 계산이 필요하고 좀 귀찮음
보면 알 수 있듯이, 각각의 방법마다 장단점이 명확하다.
즉, 완벽한 방법은 없다는것!
그러니 우린 모든 방법을 숙지하고 상황에 맞는 최적의 방법을 사용할 수 있어야한다.
Recursion Tree Method
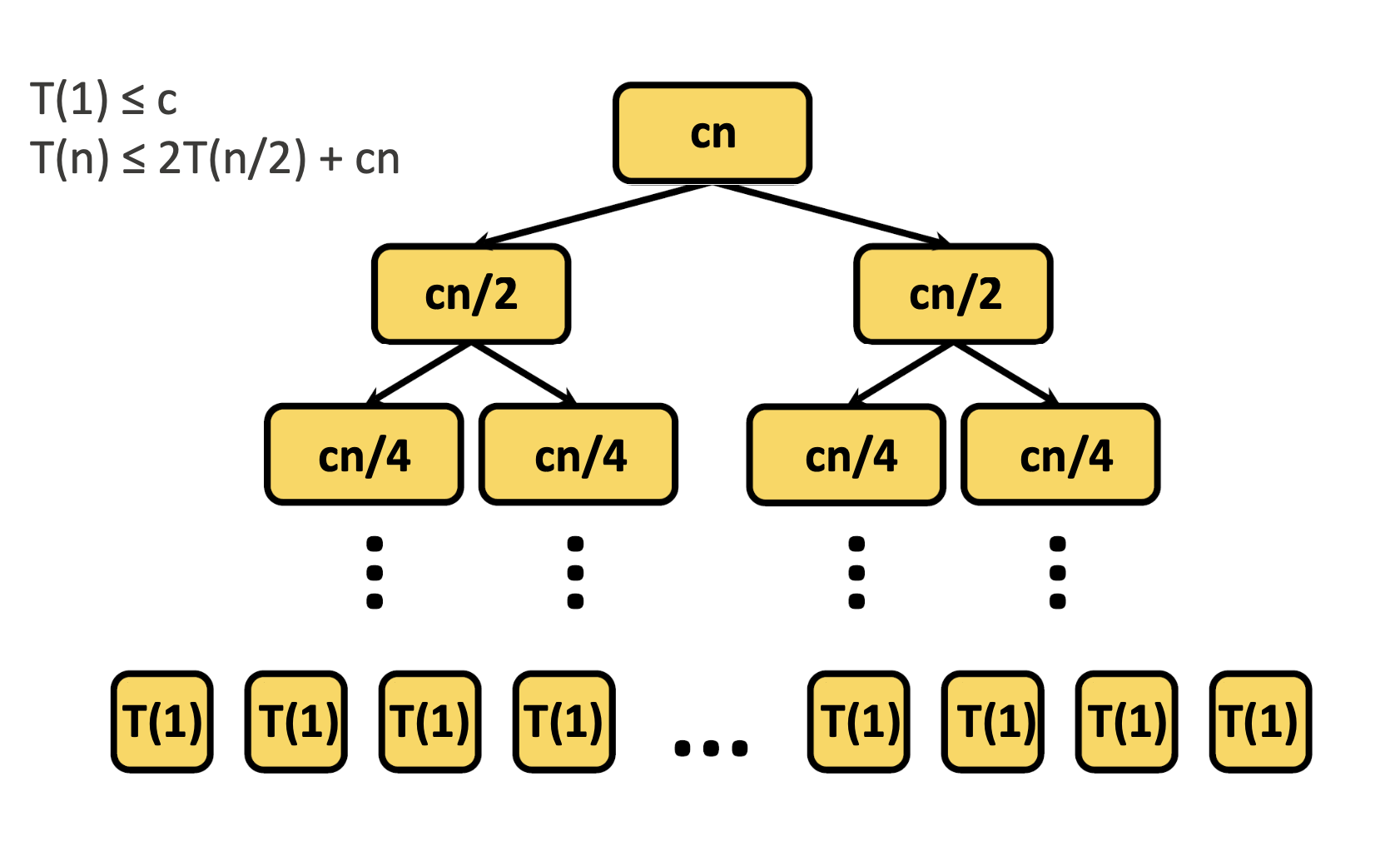
중요한 점은 각 레벨마다 총합시간은 cn으로 일정하다는 것이다.
그리고 트리의 깊이는 log₂n이다
cn ÷ 2ⁱ = 1
→ cn =2ⁱ
→ log₂ n = i
1. 각 레벨별 실행 시간은 항상 cn이다
맨 위 레벨: cn
그 다음 레벨: cn/2 + cn/2 = cn
그 다음도 cn/4 + cn/4 + cn/4 + cn/4 = cn즉, 레벨이 아무리 내려가도 전체 합은 cn으로 일정.
2. 레벨의 수는 log₂n개
각 레벨마다 문제 크기가 절반으로 줄어드니까,
n → n/2 → n/4 → ... → 1 까지 몇 번 나누냐면:
n / 2ⁱ = 1 → i = log₂n
3. 전체 시간은 cn * log₂n
레벨 수가 log₂n이고, 각 레벨에서 cn 시간이 들기 때문에
총 시간: cn x log₂n
더하지 않은 루트 노드의 정렬 시간은 cn이지만
어차피 이것도 cn*log₂n 에 포함되는 수준이라
전체 시간은 Θ(n log₂n)으로 수렴함