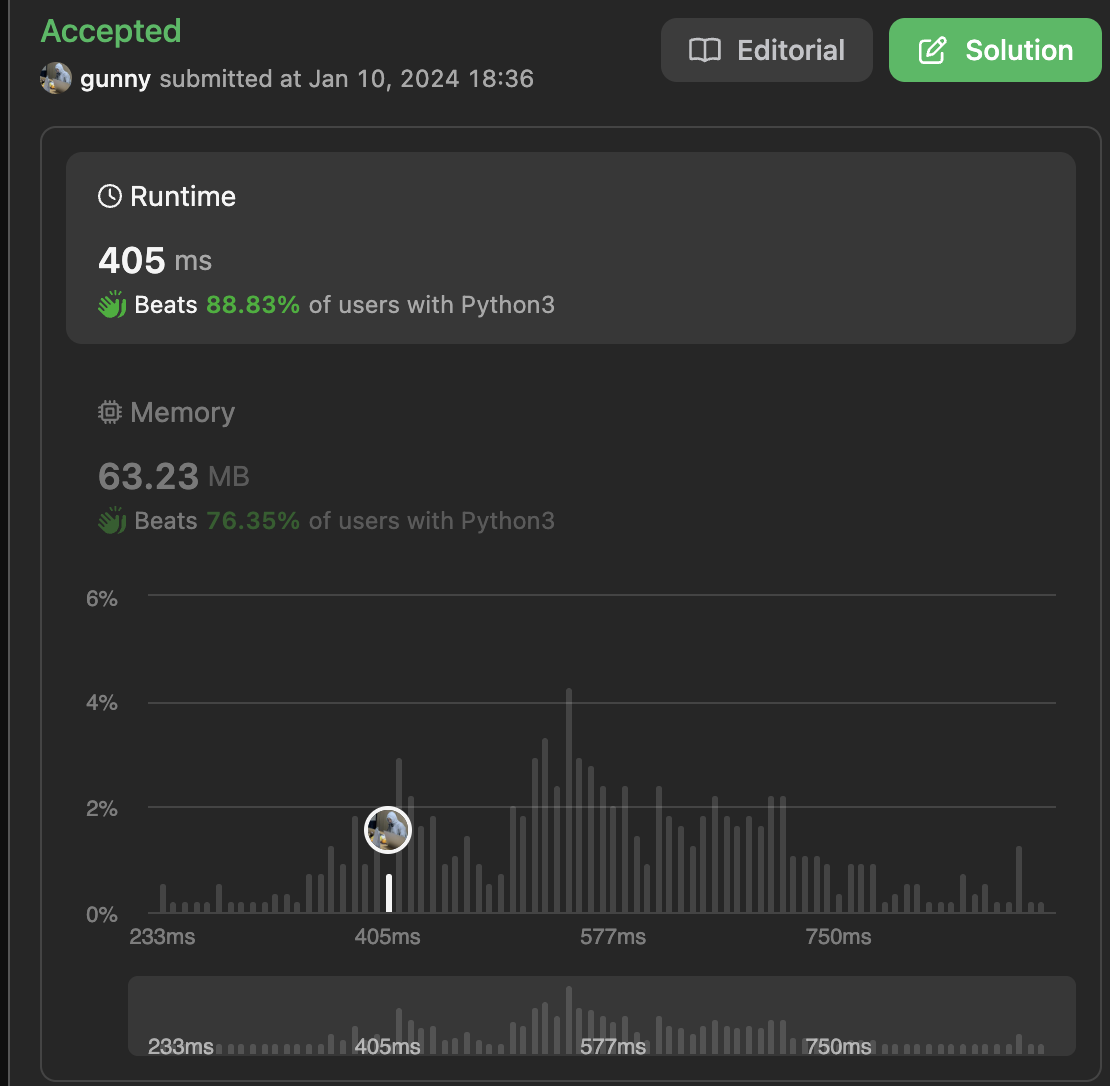
[2024] Day10. 2385. Amount of Time for Binary Tree to Be Infected

2024년부터 새롭게 다시 시작하는 코딩테스트

2024년 1월 10일 (수)
Leetcode daily problem

2385. Amount of Time for Binary Tree to Be Infected

https://leetcode.com/problems/amount-of-time-for-binary-tree-to-be-infected/description/

Problem

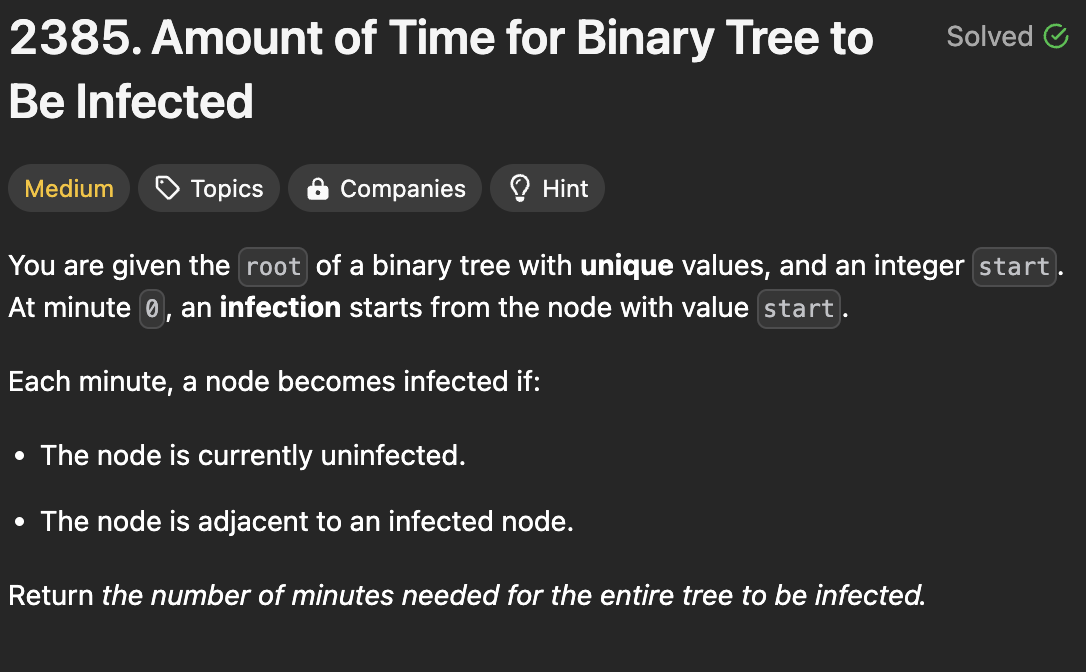
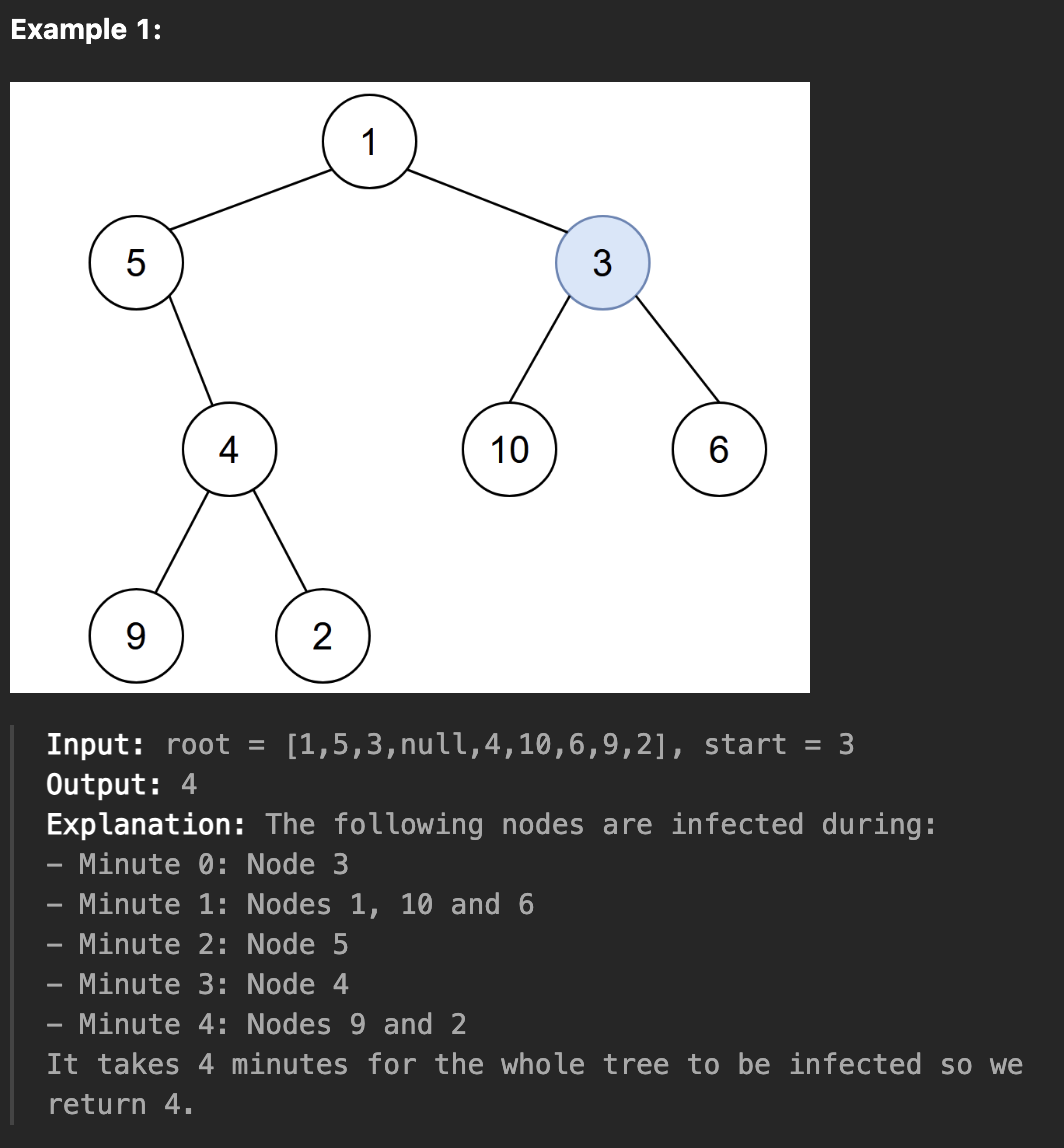
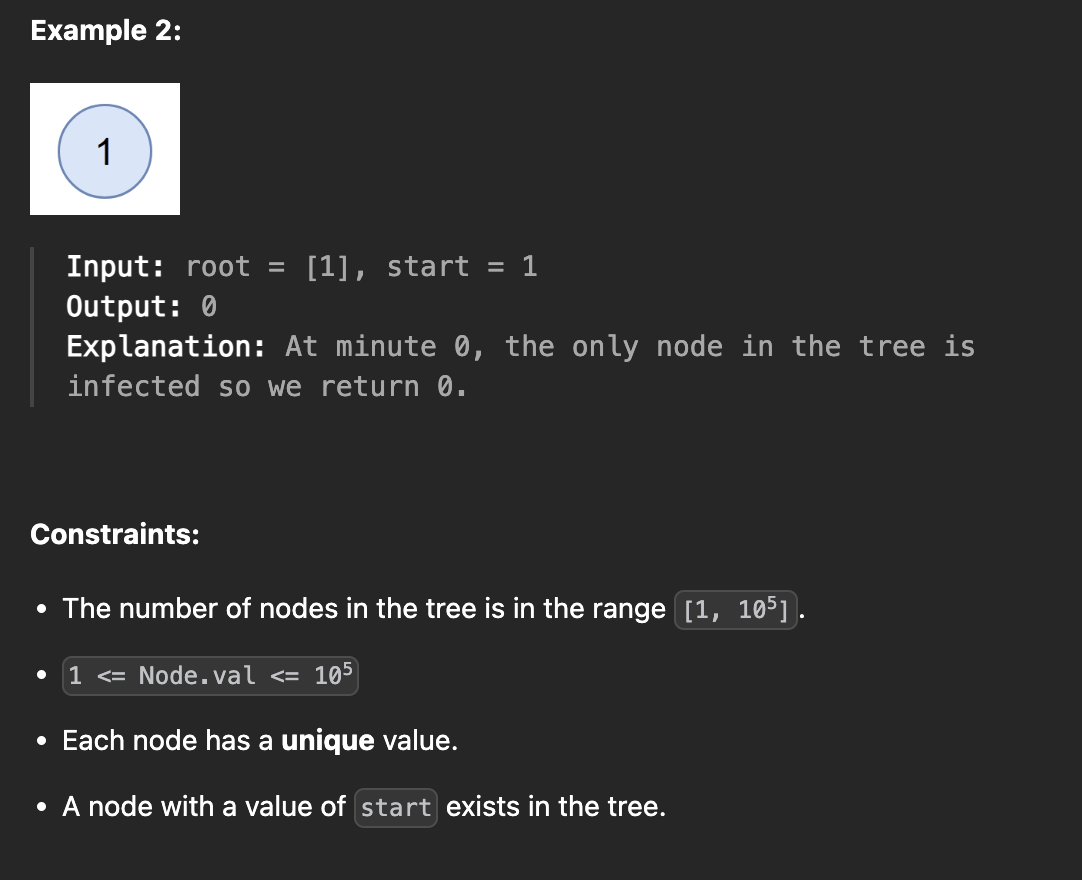
고유한 정수 값을 가지는 이진 트리가 주어진다.
트리의 노드 하나를 탐색하는데 시간이 1씩 늘어난다.
루트 노드가 아닌 랜덤의 노드에서 시작할 때, 전체 트리를 탐색하는 필요한 시간을 반환한다.

Solution

Tree (binary tree)

루트 노드를 탐색하면서, 해당 노드에 해당하는 left, right 노드에 대해 저장한다.
queue 를 생성하고, 시작 노드에 따라서 노드를 탐색하면서 방문한 노드를 따로 저장하고 방문하지 않는 노드를 다 탐색할 때마다 시간을 더하고 마지막 전체 노드를 모두 반복했으면 최종 시간을 반환한다.

Code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def amountOfTime(self, root: Optional[TreeNode], start: int) -> int:
    
        def dfs(node):
            if not node:
                return
            if node.left:
                graph[node.val].append(node.left.val)
                graph[node.left.val].append(node.val)
            if node.right:
                graph[node.val].append(node.right.val)
                graph[node.right.val].append(node.val)
            dfs(node.left)
            dfs(node.right)

        graph = defaultdict(list)
        dfs(root)
        visited = set()
        queue = deque([start])
        ans = -1
        while queue:
            ans +=1
            for _ in range(len(queue)):
                cur_node = queue.popleft()
                visited.add(cur_node)
                for neighbor in graph[cur_node]:
                    if neighbor not in visited:
                        queue.append(neighbor)
        return ans
           

Complexicity

시간 복잡도

트리의 모든 노드를 한 번 방문하므로 시간 복잡도는 O(N)이다.
(N : 노드의 총 수)

공간 복잡도

그래프를 나타내기 위해 defaultdict를 사용하고, 각 노드의 이웃을 저장하는데, 이 과정에서 그래프의 공간 복잡도는 O(N)이다.
방문한 노드를 저장하는 데 사용되는 세트의 공간 복잡도는 최악의 경우 O(N)가 된다. 또한 큐에 최악의 경우 모든 노드가 들어갈 수 있으므로 큐의 공간 복잡도는 O(N)로,
따라서 전체 공간 복잡도는 O(N)이다.

---