[2024] Day9. 872. Leaf-Similar Trees

2024년부터 새롭게 다시 시작하는 코딩테스트

2024년 1월 9일 (화)
Leetcode daily problem

872. Leaf-Similar Trees

https://leetcode.com/problems/leaf-similar-trees/?envType=daily-question&envId=2024-01-09

Problem

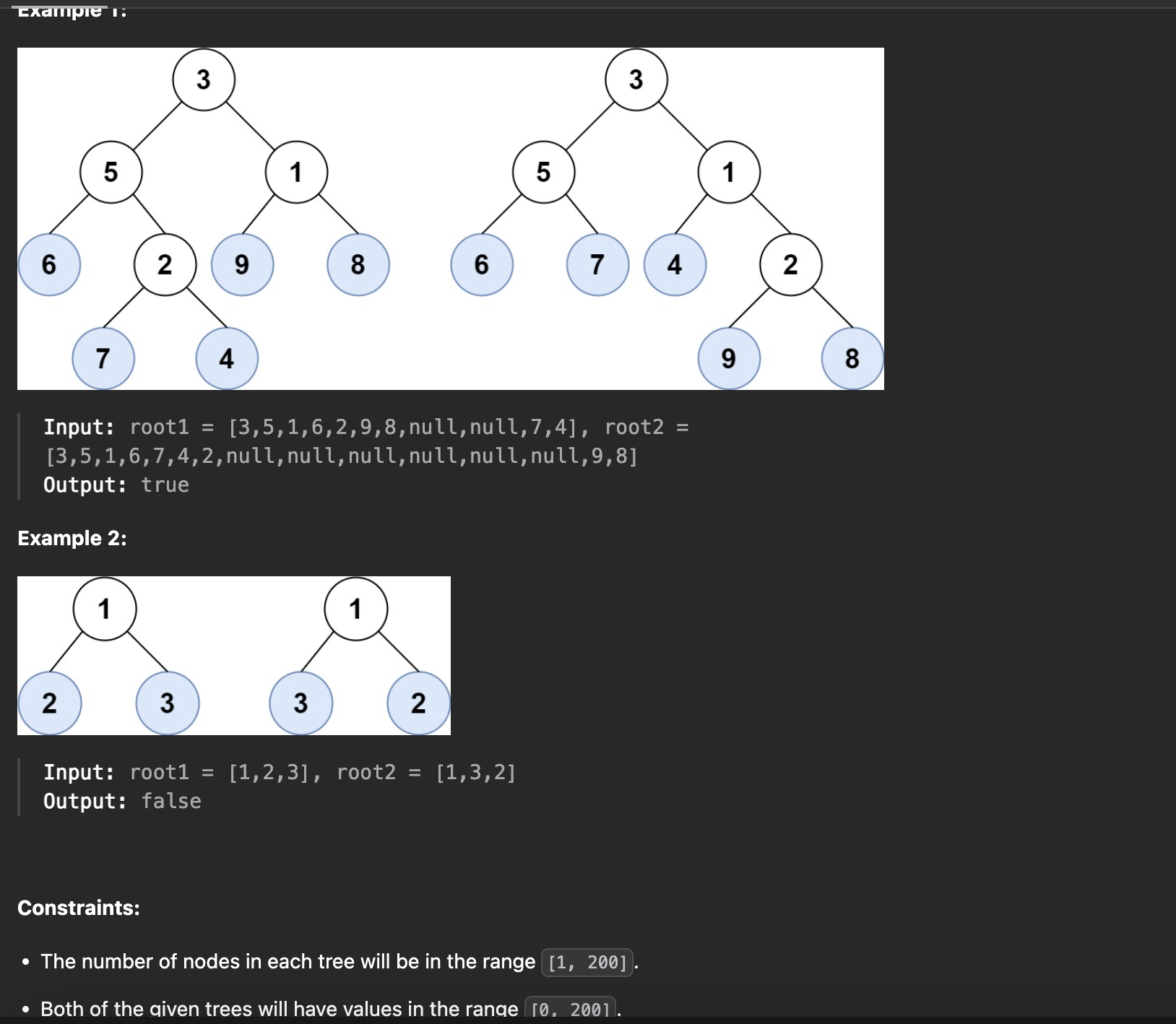
이진 트리의 모든 노드를 왼쪽에서 오른쪽 순서로 고려할 때, 위 그림의 터미널 노드는 (6, 7, 4, 9, 8)이다.

두 개의 이진 트리가 주어질 때, 터미널 노드의 순서가 동일하면 유사하다고 간주되는데, root1과 root2가 있는 두 개의 주어진 트리가 유사 노드인 경우에만 true를 반환한다.

Solution

Tree (binary tree)

dfs를 이용해서 재귀로 풀어나가는 방법으로 풀었다.
end point가 되는 node가 없을 때 빈 리스트를 반환하고
조건으로 현재 노드 기준 왼쪽, 오른쪽 노드가 없는 경우에 현재 노드의 값을 리스트에 저장해서 left, right 를 순차적으로 recursive 하게 돈다.
root1 ,root2를 해당 dfs로 탐색하고 나온 값이 같으면 유사노드 아니면 False를 반환한다.

Code

class Solution:
    def leafSimilar(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> bool:
        
        def dfs(node):
            if not node:
                return []

            if node.left is None and node.right is None:
                return [node.val]

            return dfs(node.left) + dfs(node.right)


        return dfs(root1) == dfs(root2)     

Complexicity

시간 복잡도

이진 트리의 모든 리프 노드를 찾는 과정에서 각 노드를 한 번 탐색한다.
따라서 트리의 모든 노드를 한 번씩 방문하는 시간 복잡도는 O(N)이다.
N : 트리의 전체 노드 수

공간 복잡도

재귀 함수인 dfs가 호출될 때마다 스택에 새로운 호출이 추가된다.
트리의 높이에 비례하는 stack 프레임이 쌓이게 되고,
최악의 경우 트리가 한쪽으로 편향되어 있을 때 stack의 깊이가 트리의 높이와 같아지므로 공간 복잡도는 O(H) 이다.
H: 트리의 높이

그러나 주어진 코드에서는 터미널 노드만을 대상으로 재귀 호출이 이루어지므로,
스택의 깊이는 트리의 높이보다 작거나 같기 때문에 실제로는 O(H)보다 작은 공간이 필요하다.

최종적으로 시간 복잡도는 O(N), 공간 복잡도는 O(H) 이다.

---