[2024] Day8. 938. Range Sum of BST

2024년부터 새롭게 다시 시작하는 코딩테스트

2024년 1월 8일 (월)
Leetcode daily problem

938. Range Sum of BST

https://leetcode.com/problems/arithmetic-slices-ii-subsequence/

Problem

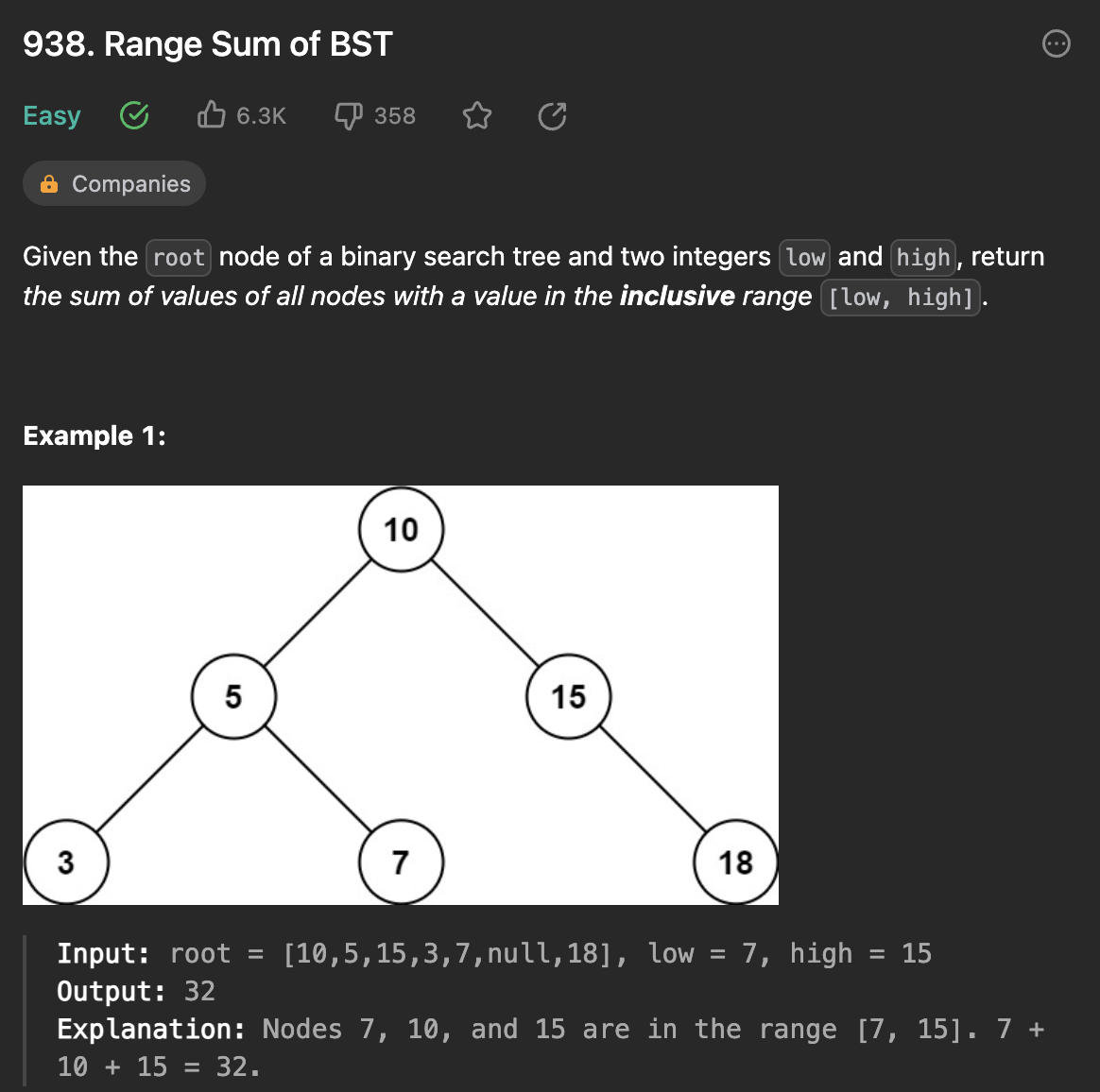
이진 검색 트리(BST)가 주어지고, 트리에서 주어진 범위(low, high) 내에 있는 노드 값들의 합을 계산한다.

Solution

Graph ( binary search Tree)

(1) 재귀로 푸는 방법
(2) stack을 이용하는 방법
(3) queue를 이용하는 방법
(4) for문을 이용하는 방법

다양하다.

일단 재귀로 푸는 방법으로 풀기

Code

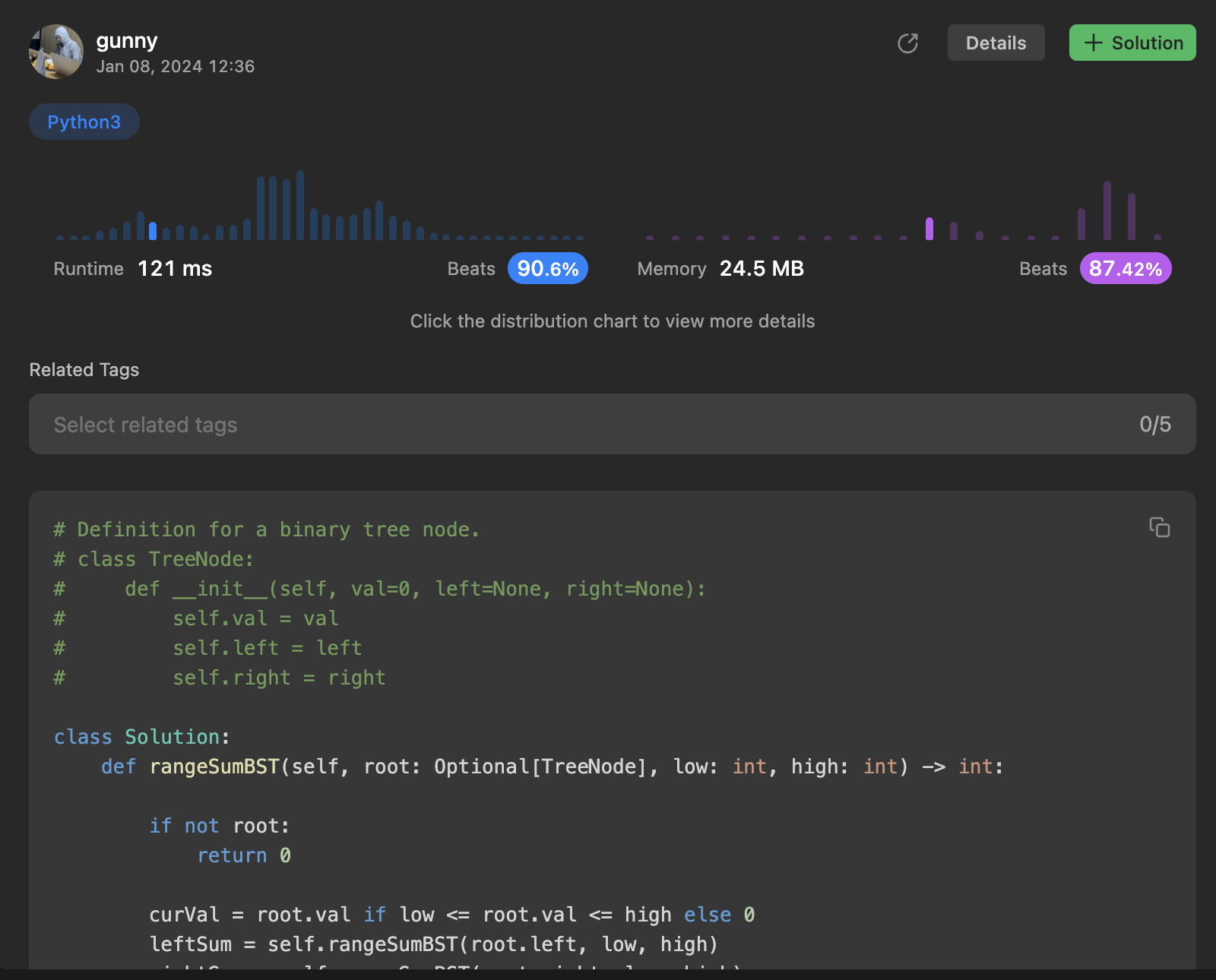
class Solution:
    def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:
        
        if not root:
            return 0

        curVal = root.val if low <= root.val <= high else 0
        
        leftSum = self.rangeSumBST(root.left, low, high)
        rightSum = self.rangeSumBST(root.right, low, high)

        return curVal + leftSum + rightSum    

Complexicity

시간 복잡도

시간복잡도는 트리의 노드 수에 비례하므로,
트리의 높이를 H라고 하면, 시간복잡도는 O(H)이다.
만약 트리가 균형 잡힌 이진 검색 트리라면 H는 O(logn) 이고,
비균형 트리의 경우 H는 O(n)이 될 수 있다.

공간 복잡도

재귀적인 방법을 사용하고 있어, 재귀 호출 스택에 필요한 공간이 추가로 사용된다. 트리 높이에 비례하는 스택 공간이 필요해서 최악의 경우 O(H) 가 필요하고, 호출이 트리의 깊이와 관련되어있어서 최악의 경우 O(n)이 발생한다.

---

• 추가적으로 stack 이나 queue를 이용한 방법은 유사하다

stack

class Solution:
    def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:
        stack = [root]
        totalSum = 0

        while stack:
            node = stack.pop()
            if node:
                if low<=node.val<=high:
                    totalSum += node.val
                if node.val > low:
                    stack.append(node.left)
                if node.val < high:
                    stack.append(node.right)
        
        return totalSum

queue

class Solution:
    def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:
        queue = deque([root])
        totalSum = 0

        while queue:
            node = queue.popleft()
            if node:
                if low<=node.val<=high:
                    totalSum += node.val
                if node.val > low:
                    queue.append(node.left)
                if node.val < high:
                    queue.append(node.right)

        return totalSum