2024년부터 새롭게 다시 시작하는 코딩테스트
2024년 6월 27일 (목)
Leetcode daily problem
1791. Find Center of Star Graph
https://leetcode.com/problems/find-center-of-star-graph/?envType=daily-question&envId=2024-06-27
Problem
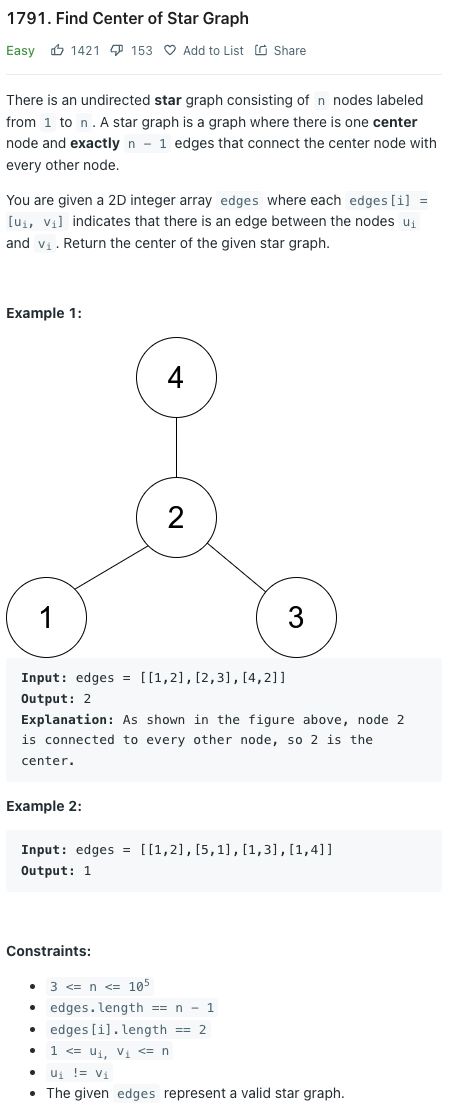
1부터 n까지 레이블이 지정된 n개의 노드로 구성된 방향이 없는 별 그래프가 있습니다. 별형 그래프는 하나의 중심 노드가 있고 중심 노드를 다른 모든 노드와 연결하는 정확히 n - 1개의 간선이 있는 그래프이다.
각 edge[i] = [ui, vi]는 노드 ui와 vi 사이에 가장자리가 있음을 나타내는 2차원의 정수 배열 edges가 주어질 때 주어진 별 그래프의 중심을 반환한다.
Solution
graph degree, greedy
별 그래프의 중심 노드는 다른 모든 노드와 연결되어 있어 n-1의 연결을 가지고 있고, 다른 노드들은 각 하나의 연결만을 가지고 있다는 걸 알 수 있다.
즉, 노드가 가지는 연결 수인(차수)가 중심노듣 n-1, 다른노드는 1인 것이다.
중심 노드를 찾기 위해서 각 노드의 차수를 세고, 모든 edge를 반복하면서 각 edge가 연결하는 두 노드의 차수의 카운터를 업데이트하여 맵에 저장하고, 해당 차수가 n-1인 노드를 찾는 것이다.
class Solution:
def findCenter(self, edges: List[List[int]]) -> int:
degree_map = {}
for edge in edges:
degree_map[edge[0]] = degree_map.get(edge[0], 0) +1
degree_map[edge[1]] = degree_map.get(edge[1], 0) +1
for node, cnt in degree_map.items():
if cnt == len(edges):
return node
return -1해당 코드에서 edge를 순회하면서 degree의 맵을 채우고 있는데, edges 리스트의 모든 edge를 순회하므로 시간 복잡도는 O(n) 이다.
추후 저장한 degree_map을 순회하면서 중심 노드를 찾고 있기 때문에 최대 n개의 노드를 순회하여 시간 복잡도는 O(n)가 소요된다.
즉 전체 시간 복잡도는 O(n) 이다.
여기서 degree_map에서 n개의 노드를 저장할 수 있으므 공간복잡도는 O(n) 이고 나머지는 상수공간이므로 최종 공간복잡도는 O(n) 이다.
각 시간 복잡도와 공간복잡도가 O(n)이 소요될 때,
이를 최적화 하는 방법으로 greedy 방법을 사용해본다면 아래와 같다.
Code
class Solution:
def findCenter(self, edges: List[List[int]]) -> int:
edge1, edge2 = edges[0], edges[1]
return edge1[0] if edge1[0] in edge2 else edge1[1]별 그래프에서 중심 노드가 모든 edge에 나타나므로, 각 노드의 차수를 계산하지 않고 모든 edge에 나타나는 노드를 찾으면 해당 노드가 중심 노드이다.
주어진 배열의 임의의 두 edge만 확인해서 이 edge의 공통 노드는 중심노드가 될 것이므로 차수를 셀 때보다 더 적은 시간 및 공간이 필요된다.
Complexicity
시간 복잡도
기존 배열의 첫 번째, 두 번째 edge로 요소가 포함되어 있는지를 확인하는 조건으로 해당 비교는 시간복잡도 O(1) 이다.
공간 복잡도
각 기존 배열의 처음과 두번째 요소를 가리키는 변수들로, 추가적인 메모리 사용이 거의 없어 공간 복잡도에 영향을 미치지 않는다. 즉 공간 복잡도는 O(1)이다.
