[2024] day 181. Leetcode 2285. Maximum Total Importance of Roads

2024년부터 새롭게 다시 시작하는 코딩테스트

2024년 6월 28일 (금)
Leetcode daily problem

2285. Maximum Total Importance of Roads

https://leetcode.com/problems/maximum-total-importance-of-roads/?envType=daily-question&envId=2024-06-28

Problem

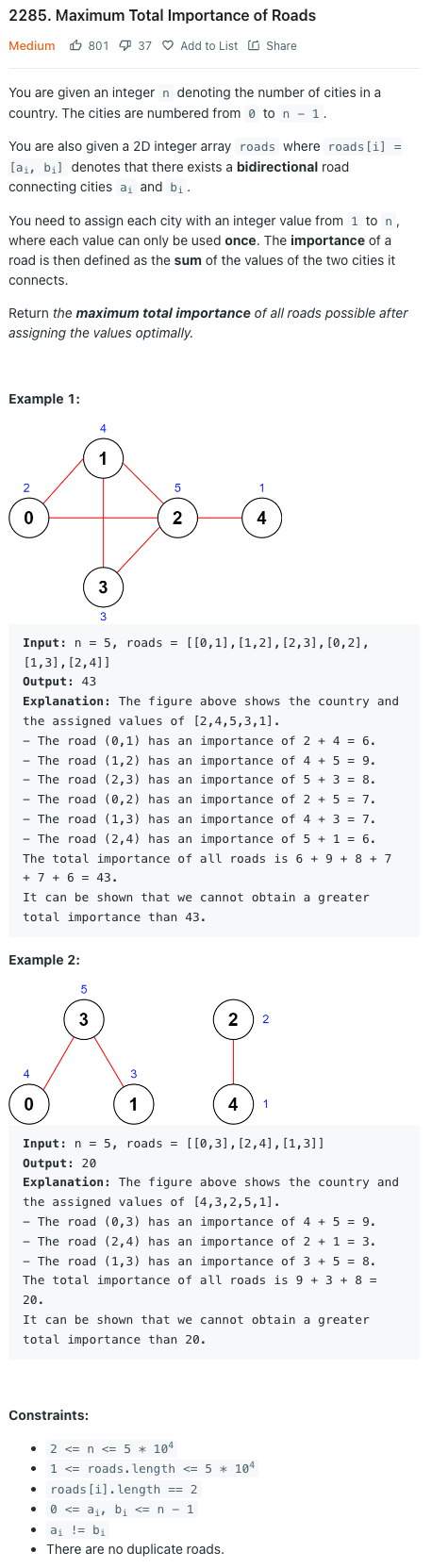
한 국가의 도시 수를 나타내는 정수 n이 주어지고 도시에는 0부터 n-1까지 번호가 매겨져 있다.

roads[i] = [ai, bi]는 도시 ai와 bi를 연결하는 양방향 도로가 있음을 나타내는 2D 정수 배열이다.

각 도시에 1부터 n까지의 정수 값을 할당해야 하며, 각 값은 한 번만 사용할 수 있다. 도로의 infortance는 도로가 연결하는 두 도시의 가치의 합으로 정의되는데, 값을 최적으로 할당한 후 가능한 모든 도로의 최대 총 중요도를 반환한다.

Solution

Sorting

노드에 1부터 N까지의 고유한 값을 할당하여 각 간선의 중요도(간선이 연결하는 노드들의 값의 합)를 최대화하는 식으로 접근한다.

먼저 각 노드의 차수(연결된 간선의 수)를 계산하는데, 노드가 더 많은 연결을 가진 경우 더 높은 값이 할당될 것이다.

계산된 노드의 차수를 기준으로 노드들을 오름차순으로 정렬한다면, 차수가 낮은 노드부터 순서대로 정렬되므로, 정렬된 차수에 따라 1부터 N까지의 값을 노드에 할당한다. 이 방식은 차수가 낮은 노드부터 값이 할당되어 높은 차수를 가진 노드들에게 높은 값이 할당되도록 하여 간선의 중요도를 최대화하려는 전략이다.

값을 할당하고 모든 간선의 최대 중요도를 계산한다. 각 간선의 중요도는 연결된 노드들의 값의 합이고, 이를 계산하여 총 중요도를 구한다.

Code

class Solution:
    def maximumImportance(self, n: int, roads: List[List[int]]) -> int:
        degrees = [0] * n
        
        for edge in roads:
            degrees[edge[0]] +=1
            degrees[edge[1]] +=1
            
        degrees.sort()
        
        value = 1
        ans = 0
        
        for degree in degrees:
            ans += value * degree
            value +=1
            
        return ans

Complexicity

시간 복잡도

노드의 차수를 찾기 위해 배열 roads를 순회하는데 O(n)이 소요되고, 배열을 오름차순으로 정렬하는 작업은 O(nlogn)이 소요된다.
아래에서 차수 배열 degrees 탐색 역시 n개의 요소를 가지고 있어 O(n)이 소요되므로, 즉 전체 시간 복잡도는 O(nlogn)이다.

공간 복잡도

차수를 저장하는 degrees는 n만큼의 공간을 차지하므로 O(n)이 필요로하다. 전체 공간복잡도는 O(n) 이다.