[2024] day 80. Leetcode 621. Task Scheduler

gunny·2024년 3월 20일

621. Task Scheduler 621. Task Scheduler python LeetCode 621. Task Scheduler python Leetcode 621. Task Scheduler

코딩테스트

목록 보기

393/530

2024년부터 새롭게 다시 시작하는 코딩테스트

2024년 3월 19일 (화)
Leetcode daily problem

621. Task Scheduler

https://leetcode.com/problems/task-scheduler/description/?envType=daily-question&envId=2024-03-19

Problem

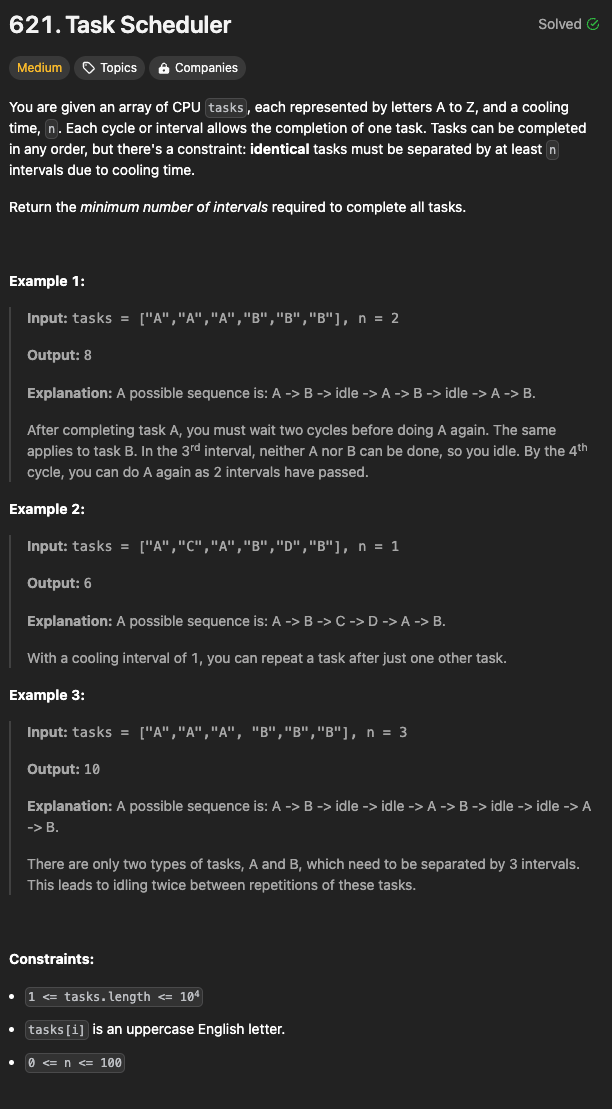
CPU 스케줄링과 유사한 작업을 수행하는데 가장 짧은 시간을 계산하는 것을 목표로 한다.
일련의 작업으로 구성된 tasks 배열이 주어질 때 각 작업은 단일 문자열로 표시되어 있다. 각 작업은 실행한 일정 시간이 있고, 이 시간은 동일 작업을 연속으로 실행할수 없도록 하는 쿨다운 시간 n이다.
작업을 실행하는 데 필요한 총 시간을 계산해야 한다. 작업은 어떤 순서로든 완료할 수 있지만 동일한 작업은 냉각 시간으로 인해 최소 n 간격으로 분리되는 것이다.

Solution

greedy algorithm, Priority queue

해당 문제는 가장 많은 빈도로 등장하는 작업을 기준으로 각 작업 사이에 냉각 시간을 넣는다. 가장 많이 등장하는 작업을 냉각 시간(cooldown) 이후에 다시 실행하도록 해야 한다.

tasks 배열의 작업 빈도를 계산하고, 가장 많이 등장하는 작업부터 처리해서 실행 순서를 결정한다음 쿨다운을 고려하여 작업을 수행한다.

먼저 그리디 알고리즘으로 접근한다면,
주어진 작업 배열을 처리하면서 가장 많이 등장하는 작업을 기즌으로 실행순서를 결정하여 "최소시간 = (가장 많이 등장하는 작업의 빈도 -1) * (쿨타임 +1) + (가장많이 등장하는 작업의 수)" 로 계산할 수 있다.

가장 많이 등장하는 작업의 빈도를 maxCnt 라고 하고,
쿨타임이 n, 가장 많이 등장하는 작업을 maxTask 라고 한다면

maxCnt - 1 : 가장 많은 빈도를 가진 작업을 제외하고 다른 작업들이 들어갈 수 있는 간격이다.
해당 작업을 실행한 뒤에는 cooldown이 필요하기 때문이다.
가장 많이 등장하는 작업이 'A' 였고 빈도가 3이었다면
A를 실행한다음 다시 A를 실행하기 까지 cooldown이 필요하므로 그 사이에 나머지 작업들이 들어간다. 이 나머지 작업들이 들어갈 수 있는 간격이므로 가장 많이 나오는 빈도에서 -1을 빼준다.
(n+1) : 한 작업을 수행하고 다음 동일 작업을 수행하기 까지의 필요한 시간이라고 보면된다.
해당 작업의 끝과 동일한 작업의 시작 사이에 cooldown이 필요한데, cooldown 길이는 작업 간의 간격이 아닌 작업을 실행한 후 다음 동일 작업을 실행하기까지의 시간을 고려한다. 그래서 각 작업 사이의 간격에 +1을 더한 값으로 계산된다.
즉 n+1은 한 작업을 실행한 후 다음 동일 작업을 실행하기 까지의 필요한 시간 간격으로, cooldown의 길이이다.

'A','A','A','B','B' 가 있다고 할 때 cooldown이 2라면

'A''A''A' 이렇게 동일한 'A' 태스크가 끝나고 다음 태크스 까지의 작업 길이는 cooldown +1이 된다.
그러므로 (n+1)을 해주는 것이다.

(maxCnt-1)*(n+1) :
위의 식을 기반으로 가장 많이 등장하는 작업들 사이에서 필요한 전체 cooldown의 시간은 최대 빈도수에서 -1을 뺀 간격에다가 cooldown의 길이를 곱한 값이다.
numTask : 가장 많이 등장하는 작업의 수로 cooldown이 필요하지 않다면 추가적인 실행이 필요한 작업의 수이다.
가장 많이 등장하는 작업을 실행하는 동안에 다른 작업들이 처리되어야 하므로, 가장 많이 등장하는 작업들을 제외한 나머지 작업을 고려해 실행 시간을 계산해야 한다.

즉, 가장 많이 등장하는 작업들 간의 cooldown 시간과 나머지 작업을 수행하는데 필요한 시간이므로 최소 실행을 계산하는 방법을 이용하여 푼다.

Code

class Solution:
    def leastInterval(self, tasks: List[str], n: int) -> int:
        taskCnt = Counter(tasks)
        maxCnt = max(taskCnt.values())
        maxTask = sum(1 for cnt in taskCnt.values() if cnt==maxCnt)
        cooldown = (maxCnt-1) * (n+1)
        minTime = cooldown + maxTasks

        return max(len(tasks), minTime)

마지막 최소 실행 시간이 주어진 작업 배열의 길이 보다 작다는 것은
cooldown을 채우는 시간 외에 더 많은 작업을 처리할 수 있다는 여유가 있는 경우를 의미한다.
최소 실행 시간이 주어진 작업의 수를 넘어선다는 것이고, 작업의 길이가 최소 실행 시간이 된다고 생각하면된다.
즉 ! 최소 실행 시간이 배열의 길이보다 작다면 cooldown을 채우는 시간외에도 더 많은 작업을 처리할 수 있는 여유가 있는 것이고, 작업 배열의 길이가 최소 실행 시간이 된다.