[Algorithm] BFS(Breadth-First Search) 너비 우선 탐색

gunny·2023년 6월 7일

BFS algorithm breadth first search 너비 우선 탐색 너비우선탐색

Algorithm

목록 보기

5/7

Algorithm - BFS(Breadth-First Search) 너비 우선 탐색 알고리즘

(1) 그래프(Graph)

그래프는 정점(node)와 정점을 연결하는 간선(edge)로 이루어진 자료구조이다.
그래프를 탐색한 다는 것은 하나의 정점에서 시작해서 차례로 모든 정점을 한 번씩 방문하는 것을 말한다.
위에서의 그래프(graph)는 트리(tree) 자료 구조와 다르다.

`graph`

노드(node)와 노드를 연결하는 간선(edge)를 하나로 모아 놓은 자료 구조
방향(Directed) 그래프, 무방향 그래프(Undirected)
cycle이 가능하고 자체 간선(self-loop)도 가능, 순환 그래프(cyclic) ,비순환 그래프(Acyclic) 모두 존재
루트 노드와 부모-자식 개념이 없다
네트워크 모델임
순회는 DFS, BFS
간선의 수는 그래프에 따라 간선의 수가 다르고, 간선이 없을 수도 있다
예시 및 종류로는 지도, 지하철 노선의 최단경로, 전기 회로 소자, 도로(교차점과 일방 통행길), 선수 과목

`tree`

그래프의 한 종류로 DAG(Directed Acyclic Graphe) 방향성이 있는 비순환 그래프의 한 정류
Directed Graph 방향 그래프이다.
cycle 불가능하고, 자체 간선(self-loop) 불가능, 비순환그래프
하나의 루트 노드만이 존재하고 모든 자식 노드는 하나의 부모 노드만을 가진다.
부모-자식 관계는 top-bottom 과 bottom-top으로 이뤄진다
계층 모델이다.
DFS, BFS 안의 pre-, in-, post-order로 순회한다.
간선의 수는 노드가 N인 트리는 항상 n-1의 간선을 가진다.
경로는 임의의 두 노드 간의 경로로 유일하다.
예시 및 종류로는 이진 트리, 이진 탐색 트리, 균형트리, 이진힙 등이 있다.

=> 정리하자면 트리는 그래프 중에서 방향성이 있는 비순환 그래프이다.

(2) BFS(Breadth-First Search) 정의

그래프를 탐색하는 방법으로 너비 우선 탐색이라고 한다.

출처 : https://developer-mac.tistory.com/64

루트 노드(혹은 다른 임의의 노드)에서 시작해서, 인접한 노드를 먼저 탐색하는 방법이다.
시작 정점으로부터 가까운 정점을 먼저 방문하고, 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법이다
주로 두 노드 사이의 최단 경로를 찾고 싶을 때 이 방법을 선택한다.
예를 들면, 지구 상에 존재하는 모든 친구 관계를 그래프로 표현한 후 'A'와 'B의 사이에 존재하는 경로를 찾을 때
: 그래프 탐색 방법중 BFS 외에 DFS(Depth-First Search) 인 깊이 우선 탐색은 모든 친구 관계를 다 살펴봐야 하지만, 너비 우선 탐색은 'A' 와 가까운 관계부터 탐색하므로 조금 더 효율적이다.
최대한 넓게 이동한 다음, 더 이상 갈 수 없을 때 아래로 이동한다.
BFS는 3가지 조건을 만족하는데 [1] 최소 비용 문제, [2] 간선의 가중치가 1, [3] 정점과 간선의 개수가 적어 시간 제약과 메모리 제한 내에 만족한다.

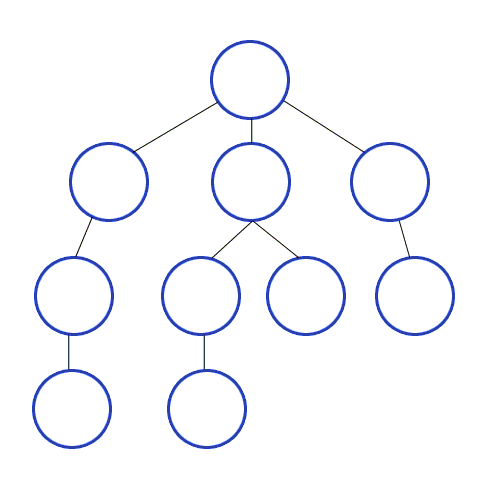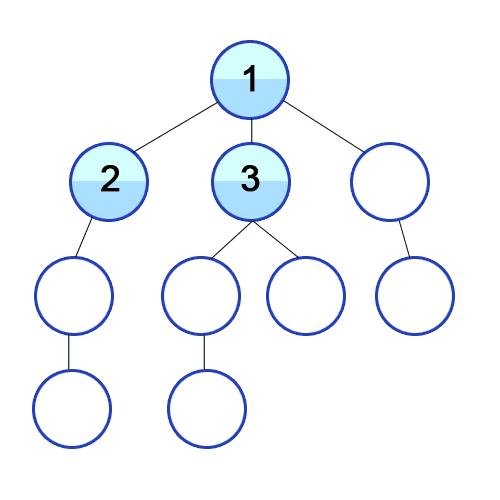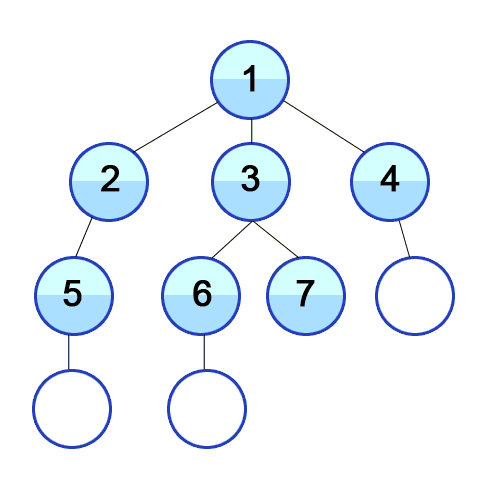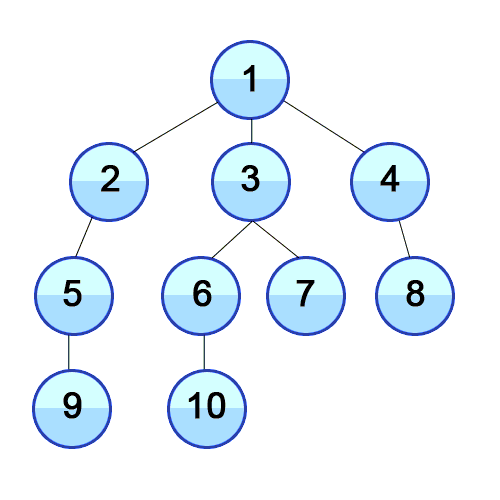
(3) BFS(Breadth-Frist Search) 탐색 방법

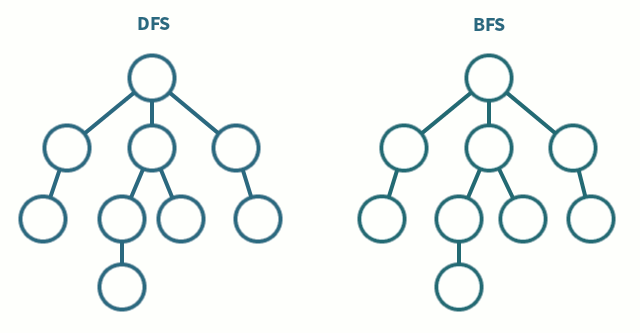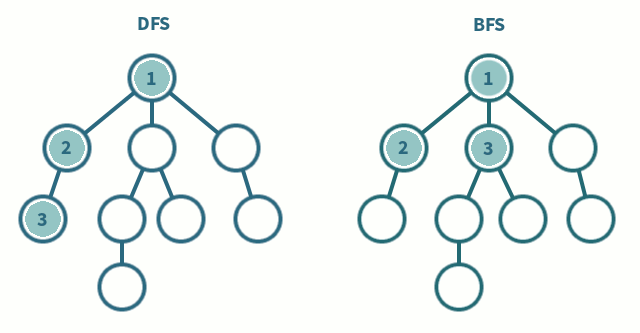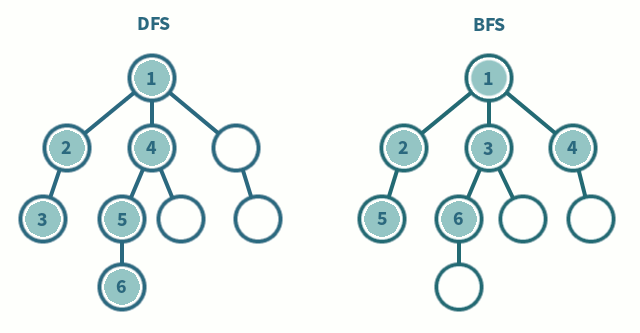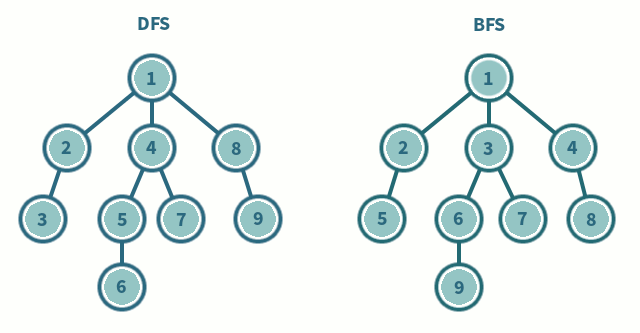
오른쪽 그림이 BFS의 탐색 방법인데,

[1] 루트 노드에서 시작
[2] 자식 노드를 ①에 저장
[3] ①에 저장된 노드들을 차례로 방문하고, 자식들을 ②에 저장
[4] ②에 저장된 노드를 차례대로 방문하고, 각각의 자식들을 ③에 저장
[5] 위 과정을 반복
[6] 모든 노드를 방문하면 탐색을 마침

DFS 와 비교하면 DFS는 갈림길에서 하나의 길로 들어서서 막다른 길이 나올 때까지 깊게 탐색한다면, BFS는 갈림길에서 연결되어 있는 모든 길을 한 번 씩 탐색한뒤 다시 연결되어 있는 모든 길을 넓게 탐색함
BFS는 현재 정점에 연결된 가까운 점들로부터 탐색함

즉, 루트 노드를 큐에 넣고 방문 처리를 하고 노드의 이웃 노드를 스택이 아닌 큐에 집어 넣어 자연스럽게 먼저 들어간 노드를 먼저 탐색(FIFO) 한다.
큐를 pop 해서 해당 노드의 방문하지 않은 모든 인접 노드를 큐에 넣고 방문 처리를 큐가 빌 때가지 반복함

(4) BFS(Breadth-Frist Search) 구현

BFS는 큐를 이용해서 구현함

class Graph:
    
    def __init__(self):
        self.graph = defaultdict(list)
        
    def addEdge(self, u, v):
        self.graph[u].append(v)
        
    def BFS(self, s):
        
        visited = [False] * (max(self.graph)+1)
        
        queue = []
        queue.append(s)
        visited[s] = True
        
        while queue:
            s = queue.pop(0)
            print(s, end = ' ')
            
            for i in self.graph[s]:
                if visited[i] == False:
                    queue.append(i)
                    visited[i] = True
                    
                    
if __name__ == '__main__':
    
    g = Graph()
    g.addEdge(0,1)
    g.addEdge(0,2)
    g.addEdge(1,2)
    g.addEdge(2,0)
    g.addEdge(2,3)
    g.addEdge(3,3)
    
    g.BFS(2)

큐를 구현시 list를 사용하면 큐의 방향에 따라 O(N)이 발생할 수 있으므로,
이중 연결 리스트인 collections.deque로 큐 구현 하기

from collections import deque

graph = [
    [],
    [2, 3, 4],
    [1, 5, 6],
    [1],
    [1, 7],
    [2, 8],
    [2, 8],
    [4],
    [5, 6]
]

queue = deque()
visited = [False] * len(graph)
queue.appendleft(1)
visited[1] =True
print(1)

while len(queue) >0 :
    cur = queue.pop()
    for s in graph[cur]:
        if visited[s]==False:
            print(s)
            queue.appendleft(s)
            visited[s] = True

(5) BFS(Breadth-First Search) 시간복잡도

N은 노드(node), E는 간선(edge) 일때,
인집 리스트는 O(N+E), 인접 행렬은 O(N^2) 이다.
일반적으로 간선(edge)의 크기가 N^2에 비해 상대적으로 적어 인접 리스트 방식이 효율적임
인접 행렬의 경우 정점의 개수 N 만큼 도는 이중 for문을 돌려 두 정점 간의 간선이 존재하는지 확인해야 해서 N의 제곱만큼 돌아서 O(N^2)이 된다.
인접 리스트로 구현되면, 존재하는 간선의 정보만 저장되어 있으면 인접 행렬에서 사용한 이중 for문이 필요하지 않는데, 다음 노드가 방문하였는지 확인할 때 간선의 개수 E의 두 배만큼의 시간이 걸린다.
각 노드를 방문할 때 정점의 개수인 N만큼 걸려서 O(N+2*E) = O(N+E)가 된다.

(6) BFS(Breadth-First Search) 문제 유형

BFS와 DFS는 특징에 따라 더 적합한 문제 유형들이 있다.
CASE 1. 그래프의 모든 정점을 방문하는 것이 주요한 문제
: BFS, DFS 편한 것 사용
CASE 2. '경로의 특징'을 저장해둬야 하는 문제
: 각 정점에 숫자가 적혀있고 a부터 b 까지 가는 경로를 구해야하는데 경로에 같은 숫자가 있으면 안되거나, 각각의 경로마다 특징을 저장해둬야 할 때는 BFS 대신 DFS 사용
=> BFS는 경로의 특징을 가지지 못함
CASE 3. 최단거리를 구해야 하는 문제
: 미로 찾기 등 최단 거리는 BFS가 유리함
=> 깊이 우선 탐색인 DFS로 경로를 탐색할 경우, 처음 발견되는 해답이 최단 거리가 아닐 수 있지만 BFS로 탐색한 경우 현재 노드에서 가장 가까운 곳부터 찾기 때문에 경로 탐색 시 먼저 찾아지는 해답이 곧 최단거리임
그 외에 검색 대상 그래프가 너무 크다면 DFS, 검색 대상의 규모가 크지 않고 검색 시작 지점으로부터 원하는 대상이 별로 멀지 않다면 BFS를 사용한다.

(7) BFS(Breadth-First Search)

Medium (Lv2) - (1)

프로그래머스 게임 맵 최단거리와 Leetcode 1091. Shortest Path in Binary Matrix

프로그래머스 게임 맵 최단거리 :
https://school.programmers.co.kr/learn/courses/30/lessons/1844

프로그래머스의 "게임 맵 최단거리" 문제는 주어진 게임 맵에서 시작 지점부터 목적지까지의 최단 거리를 찾는 문제이다. 이 문제는 2차원 배열로 표현된 맵에서 이동 가능한 칸(값이 1인 칸)으로만 이동하여 최단 거리를 구하는 것이 목표이다. 만약 시작 지점부터 목적 지점까지 이동할 수 없는 경우 -1을 반환한다.

def solution(maps):
    if maps[0][0] == 0 or maps[-1][-1] == 0:
        return -1
    
    ROWS, COLS = len(maps), len(maps[0])
    visited = [[0]*COLS for _ in range(ROWS)]
    
    queue = [(0,0,1)]
    visited[0][0] =1
    
    while queue:
        x,y,d = queue.pop(0)
        if x==ROWS-1 and y==COLS-1:
            return d
        
        for i,j in [(1,0), (-1,0), (0,1), (0,-1)]:
            if 0<=x+i<ROWS and 0<=y+j<COLS:
                if visited[x+i][y+j] == 0 and maps[x+i][y+j] == 1:
                    queue.append((x+i, y+j, d+1))
                    visited[x+i][y+j] = 1
    
    return -1

Leetcode 1091. Shortest Path in Binary Matrix :
https://leetcode.com/problems/shortest-path-in-binary-matrix/

class Solution:
    def shortestPathBinaryMatrix(self, grid: List[List[int]]) -> int:
        ROWS, COLS = len(grid), len(grid[0])
        visited = [[0] * COLS for _ in range(ROWS)]
        
        if grid[0][0] or grid[-1][-1]==1:
            return -1
 
        queue = [(0,0,1)]
        visited[0][0] = 1
        
        while queue:
            x,y,d = queue.pop(0)
            if x==ROWS-1 and y==COLS-1:
                return d
            
            for i in range(-1,2):
                for j in range(-1,2):
                    if 0<=x+i<ROWS and 0<=y+j<COLS:
                        if visited[x+i][y+j] == 0 and grid[x+i][y+j]==0:
                            queue.append((x+i, y+j, d+1))
                            visited[x+i][y+j]=1
                            
        return -1

두 문제 모두 주어진 이진 행렬에서 시작 지점부터 목적 지점까지의 최단 경로의 길이를 계산하는 BFS(너비 우선 탐색)을 구현한다. 우선, visited 배열을 생성하여 각 위치를 방문했는지 여부를 저장한다.시작 지점과 목적 지점이 이동할 수 없는 경우, 즉 시작 지점이 1로 표시되어 있거나 목적 지점이 1로 표시되어 있는 경우에는 -1을 반환한다.
큐를 초기화하고 시작 지점을 큐에 추가한다. 시작 지점은 (0, 0)이며, 시작 지점에서부터의 거리는 1로 초기화된다. 시작 지점은 방문했음을 표시하기 위해 visited 배열에도 업데이트한다.
큐가 비어있지 않은 동안, 큐에서 하나의 위치를 꺼내어 이동 가능한 모든 방향으로 탐색한다. 이동할 수 있는 방향은 상하좌우 및 대각선 방향이다.
탐색하려는 위치가 이동 가능한 위치인지 확인하는데 유효한 범위 내에 있고, 방문하지 않은 위치이며, 장애물이 없는 경우에는 큐에 추가하고 해당 위치를 방문했음을 표시한다.
목적 지점에 도달한 경우 해당 지점까지의 거리를 반환한다.
모든 탐색이 끝났는데도 목적 지점에 도달하지 못한 경우에는 -1을 반환한다.