[Algorithm] DFS(Depth-First Search) 깊이 우선 탐색

gunny·2023년 6월 12일

DFS algorithm depth first search 깊이 우선 탐색 깊이우선탐색

Algorithm

목록 보기

6/7

Algorithm - DFS(Depth-First Search) 깊이 우선 탐색 알고리즘

(1) 그래프(Graph)

그래프는 정점(node)와 정점을 연결하는 간선(edge)로 이루어진 자료구조이다.
그래프를 탐색한 다는 것은 하나의 정점에서 시작해서 차례로 모든 정점을 한 번씩 방문하는 것을 말한다.
위에서의 그래프(graph)는 트리(tree) 자료 구조와 다르다.

`graph`

노드(node)와 노드를 연결하는 간선(edge)를 하나로 모아 놓은 자료 구조
방향(Directed) 그래프, 무방향 그래프(Undirected)
cycle이 가능하고 자체 간선(self-loop)도 가능, 순환 그래프(cyclic) ,비순환 그래프(Acyclic) 모두 존재
루트 노드와 부모-자식 개념이 없다
네트워크 모델임
순회는 DFS, BFS
간선의 수는 그래프에 따라 간선의 수가 다르고, 간선이 없을 수도 있다
예시 및 종류로는 지도, 지하철 노선의 최단경로, 전기 회로 소자, 도로(교차점과 일방 통행길), 선수 과목

`tree`

그래프의 한 종류로 DAG(Directed Acyclic Graphe) 방향성이 있는 비순환 그래프의 한 정류
Directed Graph 방향 그래프이다.
cycle 불가능하고, 자체 간선(self-loop) 불가능, 비순환그래프
하나의 루트 노드만이 존재하고 모든 자식 노드는 하나의 부모 노드만을 가진다.
부모-자식 관계는 top-bottom 과 bottom-top으로 이뤄진다
계층 모델이다.
DFS, BFS 안의 pre-, in-, post-order로 순회한다.
간선의 수는 노드가 N인 트리는 항상 n-1의 간선을 가진다.
경로는 임의의 두 노드 간의 경로로 유일하다.
예시 및 종류로는 이진 트리, 이진 탐색 트리, 균형트리, 이진힙 등이 있다.

=> 정리하자면 트리는 그래프 중에서 방향성이 있는 비순환 그래프이다.

(2) DFS(Depth-First Search) 정의

그래프를 탐색하는 방법으로 깊이 우선 탐색이라고 한다.

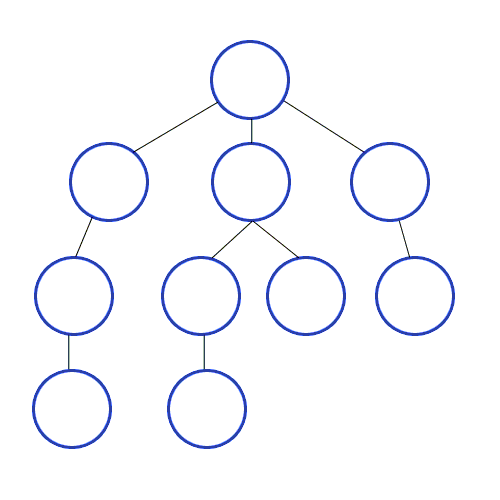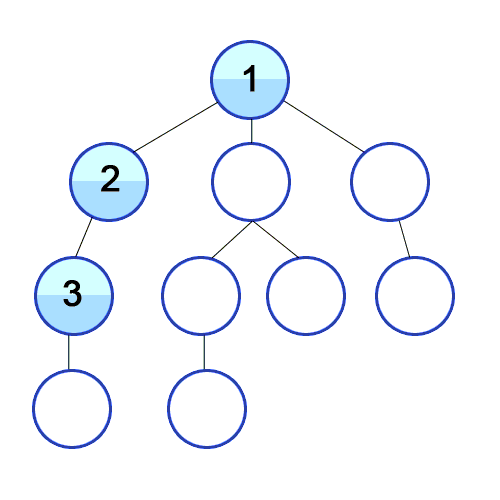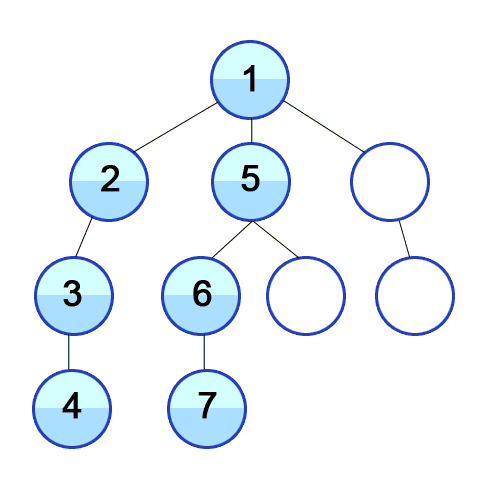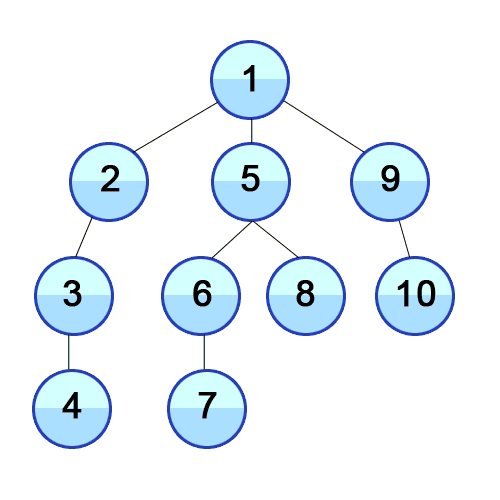
출처 : https://developer-mac.tistory.com/64

루트 노드(Root Node) 혹은 다른 임의의 Node 에서 다음 분기(Branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법
자기 자신을 호출하는 순환 알고리즘 형태
전위 순회(Pre-Order Traversals)을 포함한 다른 형태의 트리 순회는 모두 DFS의 한 종류임
이 알고리즘의 구현은, 그래프 탐색의 경우 '어떤 노드를 방문했었는지에 대한 여부를 반드시 검사' 해야 함
얻어진 해가 최단 경로가 된다는 보장이 없는데, 목표에 이르는 경로가 다수인 문제에 대해 DFS는 해에 다다르면 탐색을 끝내버려, 이때 얻어진 해는 최적이 아닐 수 있음

(3) DFS(Depth-Frist Search) 탐색 방법

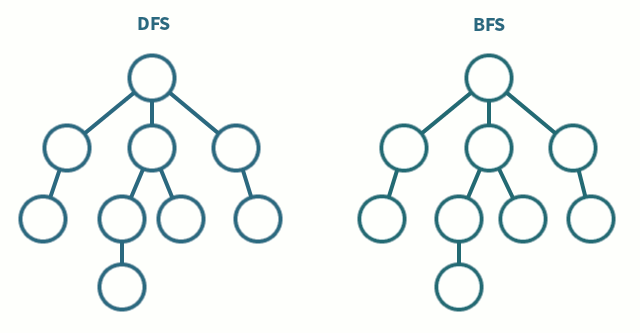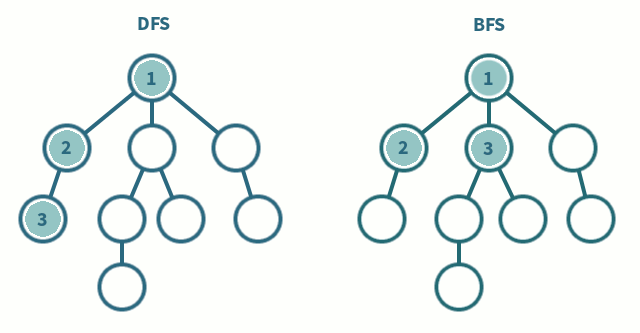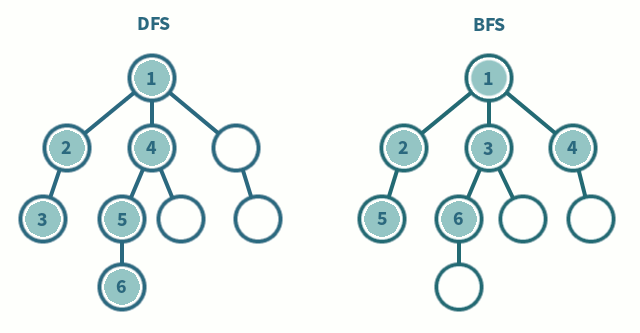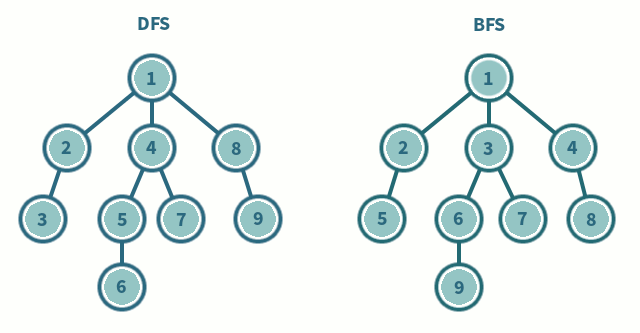
왼쪽 그림이 DFS의 탐색 방법

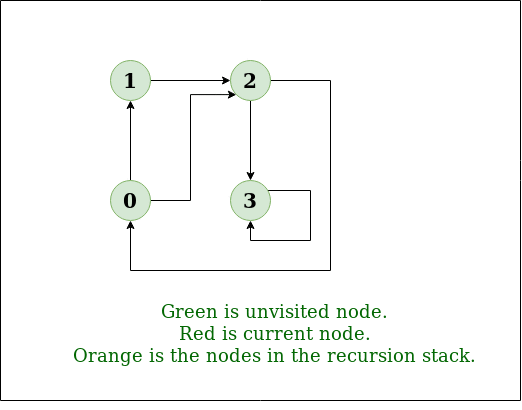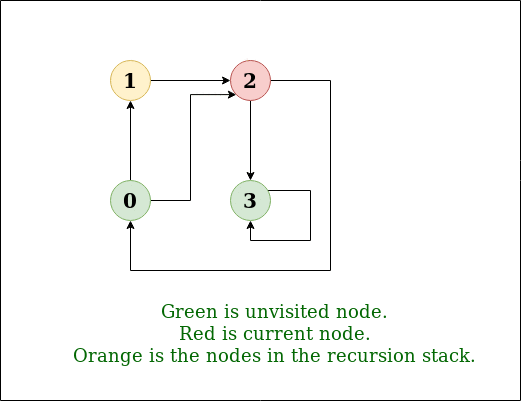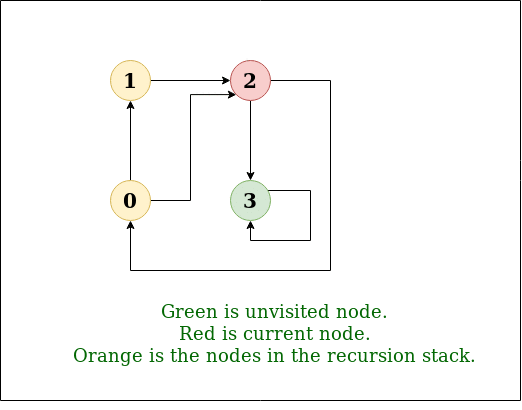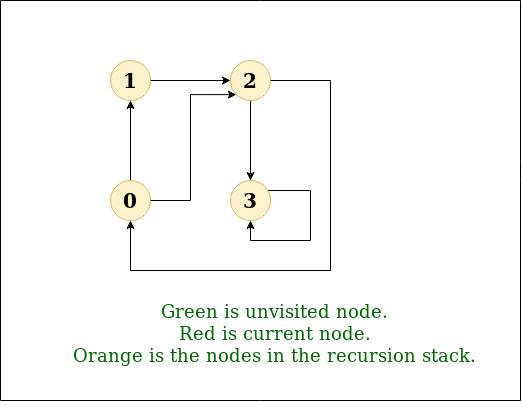
  Input: n = 4, e = 6 
  0 -> 1, 0 -> 2, 1 -> 2, 2 -> 0, 2 -> 3, 3 -> 3 
  Output: DFS from vertex 1 : 1 2 0 3

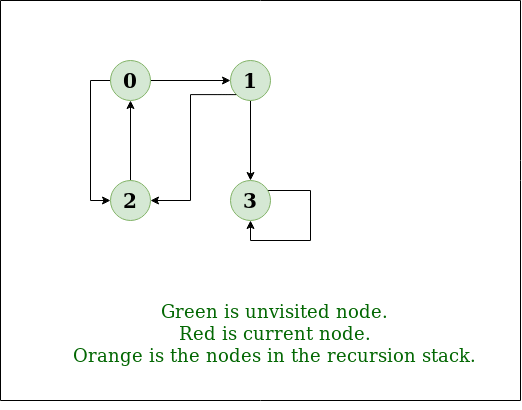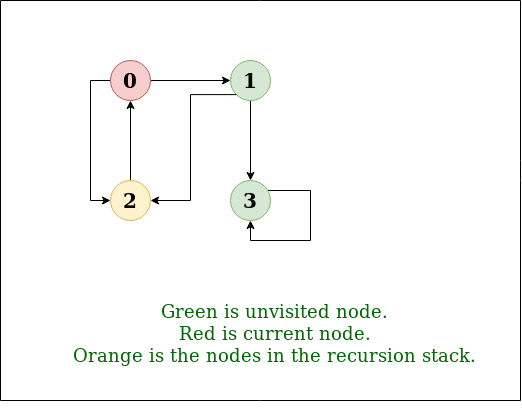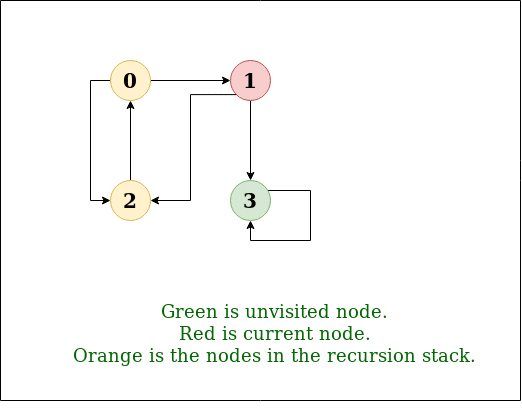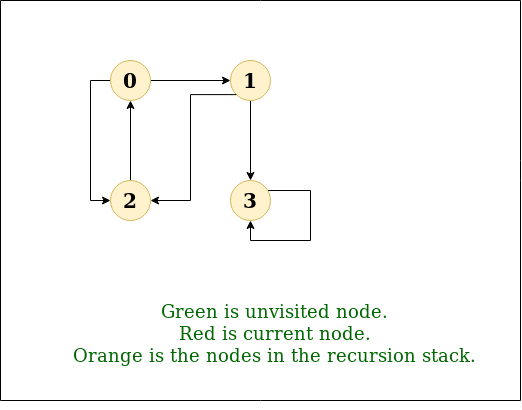
Input: n = 4, e = 6 
2 -> 0, 0 -> 2, 1 -> 2, 0 -> 1, 3 -> 3, 1 -> 3 
Output: DFS from vertex 2 : 2 0 1 3

출처 : https://www.geeksforgeeks.org/depth-first-search-or-dfs-for-a-graph/

(4) DFS(Depth-Frist Search) 구현

DFS는 Stack(스택) 혹은 재귀함수(Recursion)으로 구현함
경로를 탐색할 때 한 방향으로 갈 수 있을 때까지 가다가 더 이상 갈 수 없게 되면 다른 방향으로 다시 탐색을 진행함
모든 노드를 방문하는 경우 이 방법을 사용함

from collections import defaultdict

class Graph:
    def __init__(self):
        self.graph = defaultdict(list)
        
    def addEdge(self,u,v):
        self.graph[u].append(v)
        
    def DFSUtil(self, v, visited):
        visited.add(v)
        print(v, end=' ')
        
        for neighbour in self.graph[v]:
            if neighbour not in visited:
                self.DFSUtil(neighbour, visited)
                
    def DFS(self, v):
        visited = set()
        self.DFSUtil(v, visited)
        
    
if __name__ == "__main__":
    g = Graph()
    g.addEdge(0,1)
    g.addEdge(0,2)
    g.addEdge(1,2)
    g.addEdge(2,0)
    g.addEdge(2,3)
    g.addEdge(3,3)

    print('following is Depth First Traversal (starting from vertex 2)')

    g.DFS(2)

(5) DFS(Depth-First Search) 시간복잡도

N은 노드(node), E는 간선(edge) 일때,
인접리스트는 O(V+E), 인접 행렬 O(V^2)
그래프 내에 적은 숫자의 간선만을 가지는 희소 그래프(Sparse Graph)의 경우 인접 행렬보다 인접 리스트를 사용하는 것이 유리함
단순 검색 속도 자체는 BFS 보다 느림. 검색이 아닌 순회(traversal)을 할떄 많이 쓰임

(6) DFS(Breadth-First Search) 문제 유형

BFS와 DFS는 특징에 따라 더 적합한 문제 유형들이 있다.
CASE 1. 그래프의 모든 정점을 방문하는 것이 주요한 문제
: BFS, DFS 편한 것 사용
CASE 2. '경로의 특징'을 저장해둬야 하는 문제
: 각 정점에 숫자가 적혀있고 a부터 b 까지 가는 경로를 구해야하는데 경로에 같은 숫자가 있으면 안되거나, 각각의 경로마다 특징을 저장해둬야 할 때는 BFS 대신 DFS 사용
=> BFS는 경로의 특징을 가지지 못함
CASE 3. 최단거리를 구해야 하는 문제
: 미로 찾기 등 최단 거리는 BFS가 유리함
=> 깊이 우선 탐색인 DFS로 경로를 탐색할 경우, 처음 발견되는 해답이 최단 거리가 아닐 수 있지만 BFS로 탐색한 경우 현재 노드에서 가장 가까운 곳부터 찾기 때문에 경로 탐색 시 먼저 찾아지는 해답이 곧 최단거리임
그 외에 검색 대상 그래프가 너무 크다면 DFS, 검색 대상의 규모가 크지 않고 검색 시작 지점으로부터 원하는 대상이 별로 멀지 않다면 BFS를 사용한다.

=> 즉, DFS는 '경로의 특징'을 저장해 둬야 하는 문제나
검색 대상 그래프가 클 때 사용함