Algorithm - Two Pointers Algorithm
(1) Two-Pointer Algorithm 정의
- Two-Point Algorithm(투 포인터 알고리즘) : 1차원 배열에서 각자 다른 원소를 가리키고 있는 2개의 포인터를 조작해가면서 원하는 값을 찾을 때 까지 탐색하는 알고리즘이다.
- 리스트에 순차적으로 접근해야 할 때 두 개의 점(포인트)의 위치를 기록하면서 처리한다.
(2) Two-Pointer Algorithm 동작 방식 & 구현
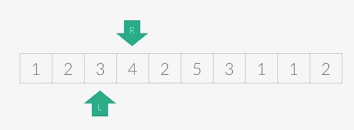
- 보통 left(l), right(r) 이나 start(s), end(d) 같은 식으로 포인트의 이름을 붙임
- 위처럼 포인트 2개를 준비한다. 여기서는 start, end 라고 명칭하겠다. 찾는 값은 target이다.
- 처음에는 start=end=0 이고, 조건은 항상 두 포인터들의 관계는 start<=end이다.
- 2개의 포인터는 현재 부분 배열의 시작(start)과 끝(end)을 가르킨다.
(3) Two-Pointer 예시
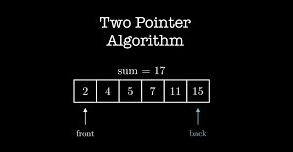
- 특정한 합을 가지는 부분 연속 수열 찾기
- 어떤 숫자들의 리스트가 주어질 때, 해당 리스트의 연속 수열의 합이 특정 값을 가지는 것을 확인하는 문제- A. 시작점과 끝점이 첫번째 원소의 인덱스를 가리키도록 함
- B-a. 현재 부분의 합이 target과 같다면 카운트
B-b. 현재 부분의 합이 target보다 작다면 end를 1 증가
B-c. 현재 부분의 합이 target보다 크다면 start를 1 증가 - C. 모든 경우를 확인할 때 까지 B를 반복
- 즉, start가 end와 같을 때 (start==end) 는, 크기가 0인 아무것도 포함하지 않는 부분 배열을 뜻하며, 다음의 과정은 start < target 인 동안 반복한다.
- 부분합이 target 이상이거나 이미 end==target인 경우 start+1- 그렇지 않다면 end+1
- 부분합이 target과 같다면 result +1
- start와 end를 증가시키는 방향으로 변화시켜 가면서 부분 배열의 합이 정확히 target이 되는 경우를 센다.
- N칸의 1차원 배열이 있을 때, 부분 배열 중 그 원소의 합이 target이 되는 경우의 수를 구하기에는 구간 합을 구간 배열로 O(1)로 구한다고 해도 경우의 수는 O(N^2)이다. 하지만 two-pointer algorithm을 사용하면 O(N) 으로 줄일 수 있다.
[시간복잡도 관련해서는 후술함]
(4) Two-Pointer 시간복잡도
- 매 루프마다 항상 두 포인터 중 하나는 1씩 증가한다. 각 포인터를 start, end라고 했을 때 start와 end는 최대 N까지 증가할 수 있고, 항상 start <= end 이다.
둘이 증가하는 과정은 최대 N번만 반복된다.
O(N^2) 가 걸리는 문제를 O(N)에 해결할 수 있음
(5) Two-Pointer 예제
[프로그래머스]
- LV 2. 구명보트
https://school.programmers.co.kr/learn/courses/30/lessons/42885 - lV 3. 보석쇼핑
https://school.programmers.co.kr/learn/courses/30/lessons/67258
[LeetCode]
[참고 사이트]
