[요약]
주요 연구 결과
- 기본 기술(산술 연산, 단위 변환 등)은 복합 추론 과제로 자발적으로 일반화되지 않는다는 것을 실험을 통해 확인
- 계층적 커리큘럼 학습(hierarchical curriculum learning)을 통해 기술 일반화를 성공적으로 유도할 수 있음
- 기본 기술 학습에서 탄탄한 기초를 다지는 것이 복합 추론 과제의 성능을 좌우하는 핵심 요소
방법론적 발견
- 기술 향상은 데이터셋과 도메인을 넘어서는 일반화 효과를 보임
- 복합 추론 과제는 기본 기술을 더욱 강화하는 데 도움을 줄 수 있음
실용적 시사점
- 계층적 커리큘럼 학습은 기술 학습과 적용 학습의 두 단계로 구성됨
- 구성 작업에 대한 지속적인 훈련은 기본 기술의 급격한 망각을 자발적으로 방지할 수 있음
- 이 연구는 복합 추론 과제를 위한 더 나은 훈련 전략을 설계하는 데 있어 중요한 지침을 제공
원문
https://arxiv.org/pdf/2403.09479
Abstract
현재의 언어 모델(LLM)은 기본적인 추론 능력을 갖추고 있음을 보여주었지만, 산술 연산이나 단위 변환과 같은 개별적인 기술을 조합해야 하는 수학 서술 문제와 같은 복잡한 추론 과제에서는 여전히 어려움을 겪고 있다. 이전 연구들은 모델의 기본 기술을 강화하거나, 이러한 기술을 복합적인 추론 과제로 일반화하는 데 충분하지 않았다.
이 논문에서는 기본 기술이 복합 추론 과제로 자발적으로 일반화될 수 있는지를 조사하기 위한 새로운 분석 프레임워크를 제안한다. 또한, 기술의 일반화 성능을 향상시키기 위해 계층적 커리큘럼 학습 전략을 도입한다. 실험 결과, 기본 기술은 복합적인 과제에 자발적으로 일반화되지 않는다는 것을 확인하였다. 하지만 계층적 커리큘럼 학습(hierarchical curriculum learning) 을 활용함으로써 일반화를 성공적으로 유도하였고, 오픈소스 언어 모델의 복합 추론 과제 성능을 크게 향상시킬 수 있었다. 더욱 고무적인 점은 이러한 기술 일반화가 데이터셋과 도메인을 넘나들며 효과적으로 작동한다는 것이다. 나아가 복합적인 추론 능력은 기본 기술을 강화하는 데도 기여할 수 있음을 확인하였다. 이 연구는 복합 추론 과제를 위한 더 나은 훈련 전략을 설계하는 데 있어 중요한 지침을 제공한다.

1. Introduction
현재의 언어 모델(LM)은 다양한 추론 과제에서 능력을 입증해왔다(Huang and Chang, 2023; Wei et al., 2022b). 그러나 산술 연산(Liu and Low, 2023; Nogueira et al., 2021; Muffo et al., 2022)과 단위 변환(Park et al., 2022) 같은 기본 기술을 결합해야 하는 수학 서술 문제(MWP, Cobbe et al., 2021; Patel et al., 2021)와 같은 복잡한 과제에서는 여전히 어려움을 겪고 있다. 기존 연구들은 현재 언어 모델이 복잡한 추론 과제에서 낮은 성능을 보이는 주요 원인을 기본 기술의 부족으로 보고 있다. 예를 들어, Fig. 1(상단)에 나타난 바와 같이, 언어 모델이 올바른 추론 과정을 따르더라도 산술 연산 및 단위 변환 기술에서의 오류로 인해 잘못된 해답을 도출하는 경우가 있다.
최근 연구들은 이러한 문제를 해결하기 위해 기술 강화에 집중하고 있지만, 여전히 한계가 존재한다. 일부 접근법은 외부 도구(Imani et al., 2023; Schick et al., 2023), 검증기(Khalifa et al., 2023) 또는 지식 베이스(Lewis et al., 2020)를 활용하여 기본 기술을 지원한다. 그러나 이러한 방법들은 외부 자원에 의존하며, 모델 자체의 기본 기술을 본질적으로 향상시키지는 못한다. 다른 연구들은 멀티태스킹 학습을 통해 성능 향상을 도모한다(Chen et al., 2023; Kim et al., 2023). 이들은 과제 간 전이 효과를 통해 기술 향상이 암묵적으로 이루어질 수 있다고 주장하지만, 어떤 기술이 향상되었는지 구체적으로 명시하지 않으며, 기술 향상이 성능에 미치는 영향을 정량적으로 평가하지 않는다. 이처럼 기술 강화는 암묵적이고 관찰이 어렵고, 과제 간 관계 역시 설명되지 않는다.
가장 관련성이 높은 기존 연구들은 특정 지식을 통합하거나(Park et al., 2022), 정교하게 설계된 연쇄적 사고(Chain-of-Thought)로 모델을 미세 조정하여(Liu and Low, 2023) 특정 기술을 개별적으로 향상시키는 데 초점을 맞춘다. 그러나 이러한 연구들은 기본 기술을 강화하면서도 모델의 기존 역량을 유지하는 데 한계를 보이며, 기술 강화가 복잡한 과제에 일반화될 수 있는지에 대한 조사는 이루어지지 않았다.
우리는 기술 강화가 복잡한 과제에 일반화될 수 있다고 주장한다. 복잡한 과제에 대한 응답 형식은 기본 기술의 조합으로 구성되기 때문이다. 예를 들어, Fig. 1에서 MWP에 대한 응답은 산술 연산과 단위 변환 기술로 구성되며, 각각 “12×37=448 cm”와 “448 데시미터(decimeters)”라는 텍스트 구간에 해당한다. 복잡한 추론 과제의 정확성은 기술 숙련도에 크게 영향을 받는다. 이 경우, 두 기술이 모두 향상되면 응답이 올바르게 도출될 것이다.
언어 모델은 특화된 학습을 통해 개별 기술을 향상시킬 수 있음이 입증되었다(Fig. 1, 중간). 우리가 특히 관심을 두는 것은 향상된 기술을 복잡한 과제에 적용할 수 있는지(Fig. 1, 하단), 즉 본 논문에서 정의한 기술 일반화이다. 우리의 연구 목표는 멀티태스킹과 근본적으로 다르며, 명시적으로 기술을 정의한다는 점이 특징이다. 더 나아가, 기술과 복잡한 과제 간의 조합 가능성으로 인해 이 일반화 효과는 관찰 가능하고 설명 가능해야 한다.
이 연구에서 우리는 수학 서술 문제(MWP)를 통한 실험적 분석으로 기술 일반화 메커니즘을 조사한다. 우리의 주요 질문은 다음과 같다. 기본 기술이 복합 추론 과제로 자발적으로 일반화될 수 있는가? , 기술 일반화 효과를 최대화하려면 어떻게 해야 하는가?
먼저, 복합 추론 과제에서 기술 일반화 메커니즘을 조사하기 위한 탐구 프레임워크를 제안한다. MWP에서 두 가지 핵심 기본 기술인 산술 연산과 단위 변환을 선정하여 분석 대상으로 삼았다. 그런 다음, 기본 기술을 강화하기 위해 필수 과제를 설계하고, 자동화된 방법으로 해당 데이터셋을 구축하였다.
더 나아가, 교육학에서의 계층적 커리큘럼 설계(White and Gagné, 1974; Scott, 2008)에서 영감을 받아 기술 일반화 효과를 극대화하기 위한 두 단계의 학습 전략인 계층적 커리큘럼 학습(hierarchical curriculum)을 제안한다.
- 첫 번째 단계는 기술 학습으로, 필수 과제에 대한 지속적인 학습을 통해 언어 모델이 기본 기술을 강화하면서도 기존 문제 해결 능력을 유지하도록 한다.
- 두 번째 단계는 적용 학습으로, 언어 모델이 강화된 기술을 복합 추론 과제에 적용하는 방법을 학습한다.
- 마지막으로, 다양한 모델을 대상으로 실험을 수행하고 상세한 분석을 진행하였다.
실험 결과 주요 관찰 내용은 다음과 같다:
(1)기본 기술은 복합 추론 과제로 자발적으로 일반화되지 않지만, 계층적 커리큘럼 학습을 통해 일반화를 유도할 수 있다.
(2) 기본 기술 학습에서 탄탄한 기초를 다지는 것이 복합 추론 과제에서 언어 모델의 성능을 좌우하는 중요한 요소이다.
(3) 기술 향상은 데이터셋과 도메인을 넘나드는 일반화 효과를 나타낸다.
(4) 반대로, 복합 추론 과제는 기본 기술을 더욱 강화하는 데 도움을 줄 수 있다. 이는 기술과 복합 과제 간의 조합 가능성에 기인한다.
우리의 기여는 다음과 같이 요약할 수 있다:
- 기본 기술에서 복합 추론 과제로의 일반화를 조사한 첫 번째 연구로서, 관련 메커니즘을 규명하였다.
- 기술 일반화의 자발성과 효과를 탐구하기 위한 탐구 프레임워크를 제안하였다.
- 기술 일반화를 유도하기 위한 계층적 커리큘럼 학습 전략을 제안하고, 실험을 통해 해당 전략이 기술 일반화에 효과적임을 입증하였다.
2. Related Work(관련 연구)
Task Generalization (과제 일반화)
과제 일반화는 이전에 학습한 지식과 기술을 새로운 타깃 과제에 효과적으로 적용하는 것을 의미한다(Talmor and Berant, 2019; Khashabi et al., 2020; Ye et al., 2021). 최근 연구들은 멀티태스킹 접근법을 활용하여 과제 간 일반화에서 큰 성과를 거두었다(Sanh et al., 2022; Wei et al., 2022a; Kim et al., 2023). Chen et al. (2023)은 일반화의 효과가 과제 간 암묵적인 기술 전이에 기인한다고 주장하며, 효과를 극대화할 최적의 학습 순서를 찾고자 한다.
본 연구는 위에서 언급한 연구들과 다음과 같은 차별점을 가진다.
- 우리는 형식적으로 조합 가능성을 가진 소스 과제와 타깃 과제를 명시적으로 사전에 정의한다.
- 대규모 과제 집합에 의존하지 않고, 기본 기술에서 복합 추론 과제로의 일반화에 초점을 맞춘다.
Compositional Generalization (구성적 일반화)
구성적 일반화 연구는 주로 의미 구문 분석에 초점을 맞추고 있다(Lake and Baroni, 2018; Keysers et al., 2020; Kim and Linzen, 2020). 이러한 연구는 데이터셋 내 분포에서 단순한 데이터를 조합을 통해 복잡한 데이터로 일반화하는 방법을 탐구한다. 반면, 본 연구는 데이터셋 간 일반화, 특히 복잡한 추론 과제에서의 기술 일반화를 탐구한다는 점에서 차별화된다.
Atomic Skill Learning (기본 기술 학습)
여러 연구는 특정 기술을 개별적으로 향상시키는 데 초점을 맞추고 있다. Liu and Low (2023)는 정교하게 설계된 연쇄적 사고(COT) 프롬프팅을 통해 언어 모델의 산술 능력을 강화하였다. Huang et al. (2023)은 차원 인식을 활용한 사전 학습 과제를 통해 단위 변환 기술을 개선하였다. 그러나 이러한 연구들은 강화된 기술을 복잡한 추론 과제로 일반화하는 가능성에 대해서는 조사하지 않았다.
Curriculum Learning (커리큘럼 학습)
커리큘럼 학습은 구조적이고 점진적으로 난이도가 증가하는 학습 경로가 학습 효과를 향상시킬 수 있음을 시사한다(Bengio et al., 2009; Wu et al., 2021). 기존 연구들은 데이터 난이도에 따라 단일 과제를 순차적으로 훈련하는 것에 중점을 두었다(Jiang et al., 2015; Xu et al., 2020; Elgaar and Amiri, 2023). 반면, 본 연구는 과제 간의 조합 가능성을 기반으로 멀티태스킹에 계층적 커리큘럼 학습을 적용하고, 이를 통해 일반화 효과를 조사함으로써 이 분야를 발전시킨다.
3. Method
본 섹션에서는 먼저 기본 기술에서 복합 추론 과제로의 일반화를 조사하기 위한 탐구 프레임워크를 제안한다(§ 3.1). 이후, 일반화 효과를 극대화하기 위한 계층적 커리큘럼 학습 전략을 제안한다(§ 3.2). 해당 프레임워크는 그림 2에 나타나 있다.
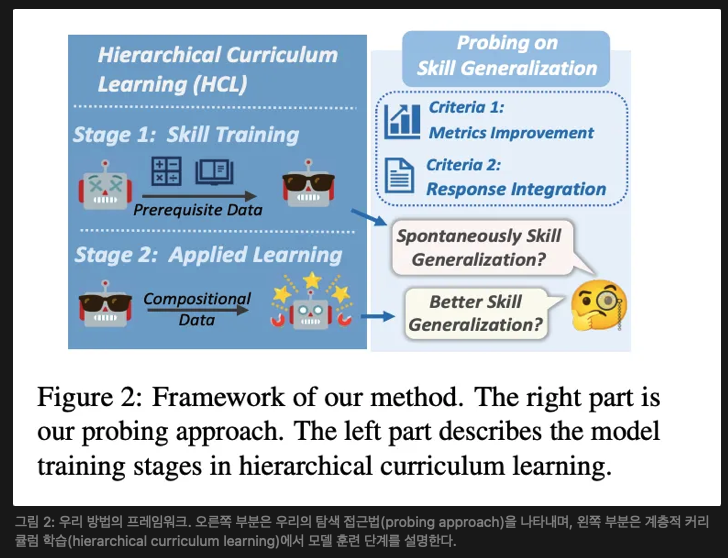
3.1 Skill Generalization Probing (기술 일반화 탐구)
3.1.1 과제 선정
우리는 수학 서술 문제(MWP, Cobbe et al., 2021; Patel et al., 2021)를 연구 과제로 선정하였다. MWP는 복합 추론의 일반적인 벤치마크로 사용되며, 정답의 정확성을 객관적으로 평가할 수 있기 때문이다.
기본 기술로는 산술 연산과 단위 변환을 선택하였다. 이는 MWP를 다룰 때 언어 모델이 이러한 기술에서 약점을 보이는 경향이 있기 때문이다(Imani et al., 2023; Schick et al., 2023; Huang et al., 2023). 모델이 해당 기술에 숙달되도록 하기 위해, 필수 과제를 설계하고 우선적으로 기술 학습을 수행해야 한다(§ 3.1.2). 이후, 향상된 모델에서 기술 일반화를 조사한다(§ 3.1.4).
3.1.2 Skill Generalization Probing (기술 탐구)
Task Selection (산술 연산 기술)
산술 연산 기술은 덧셈, 뺄셈, 곱셈, 나눗셈과 같은 숫자 간의 연산을 수행하는 능력을 의미한다. 현재 대부분의 언어 모델은 기술 중심의 특화된 학습이 부족하여 부정확한 산술 결과를 보인다(Liu and Low, 2023). 이를 개선하기 위해 산술 연산 필수 과제를 설계하고, 이에 대응하는 데이터셋을 구축하였다.
산술 데이터는 다양한 난이도를 포함하며, 연산 단계 수, 연산 유형, 값의 종류 및 유효 숫자와 같은 요소를 반영한다.
- 단순 연산에서는 모델이 산술 결과를 직접 제공하도록 요구한다.
- 복잡한 연산에서는 직접적으로 정답을 도출하는 것이 어려운 점을 고려하여, Liu and Low (2023)를 참고하여 연쇄적 사고(Chain-of-Thought, COT) 응답을 설계하였다.
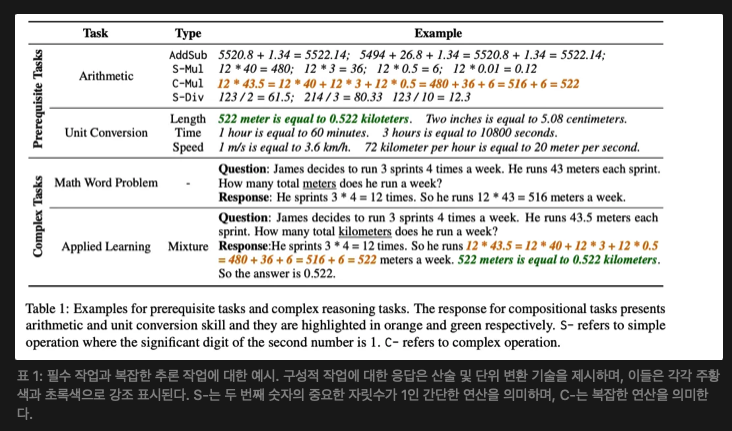
예를 들어, "12 * 43.5"라는 질문에 답할 때, 모델이 최종 정답을 제공하기 전에 분할, 확장, 항별 곱셈 및 덧셈 과정을 단계별로 제시하도록 요구한다(표 1 참고).
Unit Conversion Skill (단위 변환 기술)
산술 연산과 유사하게, 단위 변환은 MWP에서 서로 다른 단위의 값을 다룰 때 필요하다. 현재 언어 모델은 단위에 대한 충분한 지식이 부족하여 정확한 단위 변환을 수행하는 데 어려움을 겪는다(Huang et al., 2023). 따라서 단위 변환을 위한 필수 과제와 이에 대응하는 학습 데이터를 제안한다.
우리는 먼저 포괄적인 단위 지식 기반인 DimUnitKB(Huang et al., 2023)를 기반으로 MWP에서 사용되는 모든 양의 유형을 추출한다. 표 1에 나타난 것처럼, MWP에서 사용되는 단위는 길이, 시간, 속도 등 7개의 양 유형을 포함한다. 그런 다음, 같은 양 유형 아래에 있는 단위 쌍에 대해 단위 변환 데이터셋을 구축한다. 예를 들어, "미터"와 "센티미터"는 모두 길이를 나타내므로 "1 미터는 100 센티미터와 같다"는 형태로 자연스럽게 표현할 수 있다. 해당 구축 방법에 대해서는 부록 A.2에서 자세히 설명한다.
3.1.3 기술 학습( Skill Training, ST)
산술 연산과 단위 변환 데이터를 자동으로 구축할 수 있기 때문에, 이를 대량으로 생성하여 연속적인 학습을 통해 기본 기술을 언어 모델에 향상시킬 수 있다. 그러나 연속 학습은 급격한 망각, catastrophic forgetting (McCloskey and Cohen, 1989)을 일으킬 수 있다. 이를 해결하기 위해, 우리는 연속 학습에서 널리 사용되는 재생 전략, replay strategy(Ke and Liu, 2022)을 채택한다. 우리는 MWP에서 일부 학습 예제를 보존하고 이를 필수 과제 데이터와 혼합하여 모델이 기술 학습 동안 원래의 문제 해결 능력을 유지할 수 있도록 한다. 우리는 각 기술에 대해 개별적인 학습을 수행하고, 기술 혼합을 통한 학습도 진행한다.
3.1.4 기술 일반화가 이루어졌는지 어떻게 판단할 수 있을까? (How to determine whether skill generalization has been achieved?)
기술 일반화는 필수 과제에서 배운 기술을 복잡한 추론 과제에 적용할 수 있는 능력을 의미한다. 따라서 우리는 § 3.1.2에서 향상된 모델을 MWP에서 테스트하여 이를 평가할 수 있다. 다음과 같은 측면을 고려할 수 있다.
- 지표 향상(Metrics Improvement): 기술 향상은 언어 모델이 추론 과제를 해결할 때 기본 기술의 부족으로 발생한 오류를 수정할 수 있다. 따라서 이상적으로, 기술 일반화는 지표의 향상으로 반영되어야 한다.
- 응답 통합(Response Integration): 표 1에서 볼 수 있듯이, 필수 과제에서 사용하는 기본 기술의 형식은 원래 모델이 이러한 기술을 수행하는 방식과 다르다. 따라서 응답 통합이 구현되었는지 여부를 통해 이를 평가할 수 있다. 예를 들어, 성공적인 기술 일반화는 답을 직접 제공하는 대신 연쇄적 사고(COT) 형식으로 C-Mul을 수행하는 것과 관련이 있다.
3.2 계층적 커리큘럼 학습 (Hierarchical Curriculum Learning, HCL)
탐색 실험 결과, 기본적인 기술은 복잡한 작업에 자발적으로 일반화되지 않는다는 것이 나타났다.(결과는 § 5.1에 자세히 설명됨). 따라서 우리는 기술의 일반화를 유도하기 위해 계층적 커리큘럼 학습(HCL)을 제안한다.
우리의 접근법은 주로 교육학에서의 계층적 커리큘럼 설계(White and Gagné, 1974; Scott, 2008)에서 영감을 받았다. 대부분의 교육 시스템에서는 학생들이 더 고급 과정을 수강하기 전에 필수 과정을 이수합니다(Huang et al., 2005). 필수 과목은 학생들이 필요한 기초 지식과 기술을 갖추도록 보장하고, 고급 과목은 학생들이 이러한 기술을 복잡한 시나리오에 적용하는 방법을 배우도록 한다(Rovick et al., 1999). 마찬가지로, 우리는 우리의 설정에서 두 단계로 구성된 계층적 커리큘럼 학습 프레임워크를 설계하였으며, 이는 그림 2의 왼쪽이다. 첫 번째 단계는 이미 구현된 기술 훈련이다(§ 3.1.3). 우리는 LMs가 얻은 기술을 복잡한 작업에 적용할 수 있도록 하는 두 번째 단계인 응용 학습을 도입한다.
3.2.1 Applied Learning (응용 학습, AL)
이 단계에서는 먼저 응용 학습을 위한 구성적 데이터를 구성한다(표 1 하단 참조). 다음으로, 우리는 첫 번째 단계에서 모델을 구성적 데이터로 추가 훈련한다. 표 1에서 원본 MWP의 응답은 산술을 수행할 때 결과를 직접 제공한다. 또한, 응답은 보통 단위 변환 과정은 보여주지 않는다. 우리는 필수 작업에서의 응답 형식을 문제 해결 과정에 통합하여 MWP에 대해 모델이 기본적인 기술을 복잡한 작업에 적용하도록 유도한다. 데이터 구성 방법에 대한 자세한 내용은 부록 A.3을 참고한다.
4. Experimental Settings(평가 데이터셋)
4.1 Evaluation Datasets.
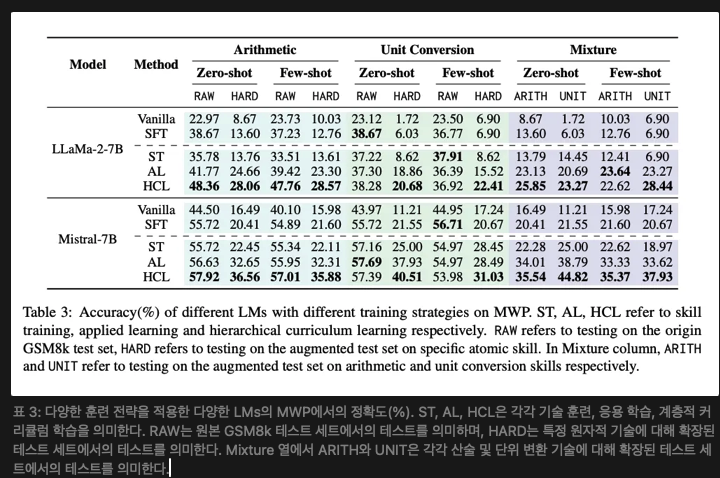
우리는 GSM8K(Cobbe et al., 2021)를 복잡한 다단계 추론을 위한 벤치마크로 선택했다. GSM8K는 산술 연산과 단위 변환 기술을 요구하는 문제를 포함하고 있다. 테스트 세트에서 산술 연산과 단위 변환에 대한 통계 자료를 수집한 결과, 난이도와 지식 범위에서 충분하지 않다는 것을 확인했다. 따라서 기술 일반화를 더욱 명확하게 보여주기 위해 GSM8K 테스트 세트의 난이도를 향상시켰다. 원본 데이터셋은 RAW, 향상된 데이터셋은 HARD로 표시된다.
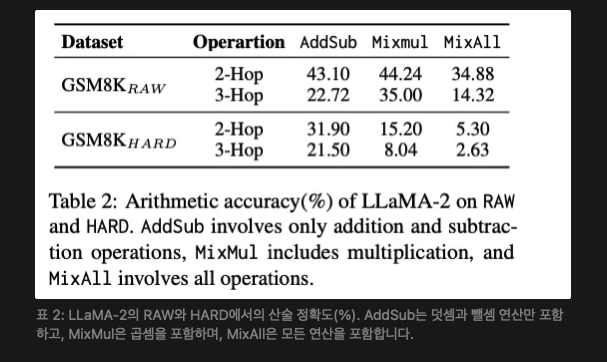
- 산술 연산 향상 (Arithmetic Augmentation) 산술 연산 기술의 난이도는 네 가지 차원에서 평가할 수 있다: 연산 단계 수, 연산 유형, 값의 종류, 유효 숫자. RAW는 첫 세 가지 차원에서 합리적인 설정을 가지고 있지만, 짧은 유효 숫자를 포함하여 산술 기술에 대한 요구가 낮다. 따라서 우리는 원래 문제의 논리를 변경하지 않고 RAW에서 유효 숫자를 확장하였다. 표 2에서는 향상 전후 LLaMA-2(Touvron et al., 2023)가 테스트 세트에서 어떻게 수행하는지 보여준다. 이 세 가지 연산의 난이도는 점진적으로 증가하지만, RAW에서 테스트하면 난이도를 구분할 수 없다. 향상된 테스트 세트는 이 난이도 경사를 반영하여 향상된 데이터셋의 효과를 입증한다.
- 단위 변환 향상(Unit Conversion Augmentation) 단위 변환의 주요 도전 과제는 단위가 표현되는 다양한 방식에 있다. 부록 B에 나타난 GSM8K 데이터의 통계 분석에 따르면, GSM8K에서 단위의 표현은 상당히 균일하여 단위 변환 기술을 완전하게 평가하기 어려웠다. 문제의 원래 의미를 변경하지 않으면서, 우리는 같은 양 유형 내에서 단위 표현을 다양화했다. 표 8은 향상된 데이터가 단위 변환 기술을 더 잘 테스트하는 방법을 보여준다.
4.2 Models and Baselines (모델 및 기준선)
우리는 서로 다른 모델 패밀리에서 두 가지 모델을 선택하여 기술 일반화를 조사했다. 해당 모델은 LLaMA-2(7B; Touvron et al., 2023)와 Mistral (7B; Jiang et al., 2023)이다. 비교한 기준선 모델은 두 가지 유형이 있다:
(1) Vanilla Model: 특별한 수정이나 향상이 없는 모델.
(2) SFT Model: MWP 훈련 세트에서 감독 학습을 통해 미세 조정된 모델.
모든 모델은 제로샷(zero-shot) 및 퓨 샷(few-shot) 프롬프트 방식으로 테스트한다. 퓨 샷 예시는 적용 학습에서 훈련 세트에서 추출된다.
5. Experimental Analysis and Findings(실험 분석 및 결과)
5.1 RQ1: 원시 작업에서 구성 작업으로의 원자 기술의 자발적 일반화가 가능한가? (RQ1: Can atomic skills generalize from prerequisite tasks to compositional tasks spontaneously?)
기본 기술은 구성 작업으로 자발적으로 일반화되지 않는다. 표 3은 다양한 언어 모델이 구성 작업에서 보인 전반적인 성능을 보여준다. 우리는 언어 모델들이 기술 훈련 후 MWP에서 눈에 띄는 성과를 얻지 못했음을 관찰한다. LLaMA-2는 HARD에서 제로샷 프롬프트로 13.60%에서 13.76%로 향상되었지만, RAW에서는 약간의 감소를 겪었다. 이 현상은 모델에 독립적이어서 기술이 메트릭 관점에서 일반화되지 않음을 의미한다. 또한, 표 4에서 볼 수 있듯이 ST 모델은 원시 작업과 전혀 다른 형식을 채택한다. 이는 기본 기술이 실제로 원시 작업에서 복잡한 작업으로 전혀 일반화되지 않음을 명확히 보여준다.
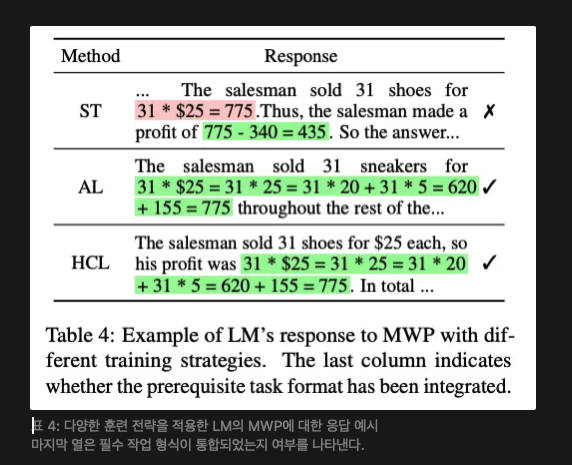
기본 기술은 적용 학습을 통해 일반화될 수 있다. HCL은 계층적 커리큘럼 학습에서 기술 일반화를 유도하기 위한 적용 학습의 두 번째 단계를 도입한다. 표 3에서 볼 수 있듯이 LLaMA-2는 HARD에서 제로샷 프롬프트로 13.60%에서 28.76%로 크게 향상되었으며, 이는 기술의 성공적인 일반화를 보여준다. 표 4의 사례 연구는 적용 학습(AL 및 HCL) 후 모델들이 원시 데이터를 MWP에 대한 응답에 통합할 수 있게 되어 정확한 계산을 수행하는 모습을 추가로 보여준다. 따라서 기술은 원시 작업에서 구성 작업으로 자발적으로 일반화되지 않지만, 적용 학습을 통해 유도될 수 있다. 또한, 우리는 이 유도된 일반화가 훈련을 통해 이루어져야 하며, 몇 샷 프롬프트로는 대체할 수 없음을 강조한다. 왜냐하면 몇 샷 학습의 메트릭은 제로샷 학습을 초과하지 않기 때문이다.
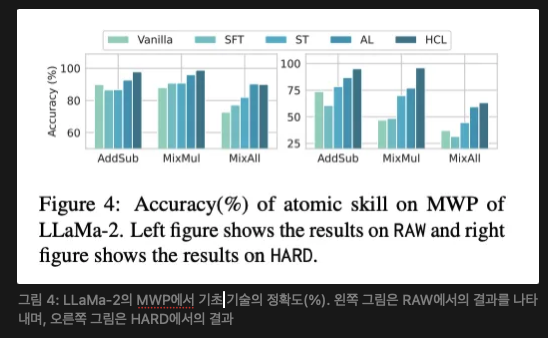
구성 작업의 향상은 기본 기술의 향상에서 비롯된다. 우리는 MWP에 대한 응답에서 기본 기술 부분을 추출하고, 그 정확도를 계산하여 그림 4에 나타낸다. 계층적 커리큘럼 학습은 모든 유형의 연산에 대해 산술 정확도의 상당한 향상을 가져왔다. 향상은 특히 MixMul과 MixAll에서 두드러져, 현재 LLM들이 이러한 산술 연산을 수행하는 데 어려움을 겪고 있음을 시사한다. 이러한 향상은 부록 D.1에서 자세히 설명된 구성 작업에 대한 답변 정확도의 향상과 일치한다.
또한, 우리는 응답에 대한 오류 분석을 수행한다. 그림 5에서 볼 수 있듯이, 먼저 응답에 기본 기술 오류가 있는지 판단하고, 그 후 다른 실수를 분류한다. 일반 모델이 저지르는 대부분의 오류는 기본 기술의 부족에서 비롯된다. HCL을 적용한 후, 일부 오류는 질문을 잘못 이해하거나 추론 오류로 바뀌었으며, 대부분의 오류는 올바른 답변으로 완전히 수정되었다. 이는 모델의 기본 기술 부족이 그 모델의 우수한 추론 능력을 가리며, HCL이 이를 효과적으로 해결할 수 있음을 보여준다.

혼합 훈련은 기술 일반화에도 효과적이다. 표 3의 세 번째 열에서 볼 수 있듯이, 혼합 훈련은 개별 훈련과 유사한 결과를 보여주며 기술 일반화를 달성한다. 제로샷 프롬프트를 사용한 LLaMA-2 모델에서 산술 성능은 13.60%에서 25.85%로 향상되었고, 단위 변환 성능은 6.03%에서 23.27%로 향상되었다. 개별 훈련과 비교했을 때, 혼합 훈련은 기술 자체의 내재적 특성에 따라 상호작용 효과를 유발한다. 결과적으로, 혼합 훈련에서의 산술 성능 향상은 개별 훈련만큼 두드러지지 않지만, 단위 변환 성능은 더 높은 향상을 보였다. 이는 향상된 산술 기술이 단위 변환에 긍정적인 영향을 미쳤기 때문일 수 있으며, 정확한 계산이 더 나은 변환을 돕기 때문이다.
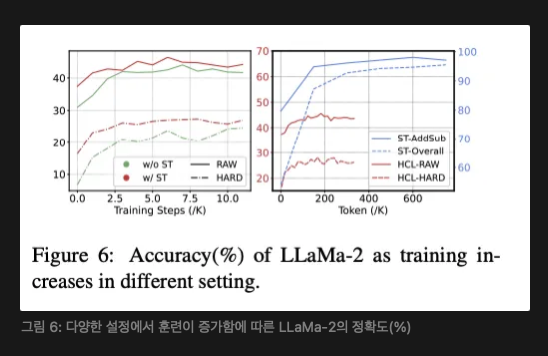
기술 학습은 HCL에서 필수적이다. 표 3에서 볼 수 있듯이, 적용 학습만의 성능은 전체 HCL보다 현저히 낮다. 그림 6 왼쪽은 훈련이 증가함에 따라 적용 학습과 HCL의 정확도를 보여주며, HCL이 더 나은 상한에 도달함을 증명한다. 우리는 이것이 적용 학습이 기술의 관련 지식을 전달하지 않고 기술의 형식적인 적용만 가르치기 때문이라고 주장한다.
또한, 우리는 적용 학습이 기술 훈련에 비해 훨씬 적은 데이터로도 수행될 수 있음을 관찰했다. 그림 6 오른쪽에서는 적용 학습이 200K 토큰 이전에 수렴하는 반면, 기술 훈련은 600K 토큰 이상을 필요로 한다. 이는 기술을 향상시키는 것이 그것을 적용하는 방법을 배우는 것보다 더 어렵다는 것을 시사한다. 이는 원시 작업을 마스터하는 것이 기본 기술을 확립하는 데 필수적이며, 그 후 빠른 적용 학습이 모델의 실제 응용 능력을 향상시킨다는 교육적 원칙을 강조한다. 실제 응용에서, 원시 데이터를 얻는 것보다 이질적인 구성 데이터의 대규모를 얻는 것이 더 어려운 경우가 많다. 데이터에 대한 수요는 데이터 수집의 어려움과 일치하며, 이는 우리의 접근 방식이 실행 가능한 방법임을 더욱 입증한다.
5.2 RQ2: 기본 기술은 데이터셋 간 또는 도메인 간 일반화를 보이는가? RQ2: Do atomic skills exhibits cross dataset or cross domain generalization?
적용 학습의 데이터가 GSM8k에서 유래한 것을 고려할 때, 우리는 기술 일반화가 분포 외 데이터(OOD)에도 효과적인지 확인하려고 한다. 우리는 OOD 데이터를 두 가지 유형으로 분류한다: 도메인 간(inter-domain)과 교차 도메인(cross-domain). 도메인 간 데이터의 경우, 우리는 SVAMP(Patel et al., 2021)과 MathQA(Amini et al., 2019)를 사용하며, 이들 모두 수학 단어 문제를 포함한다. 교차 도메인 데이터로는 MMLU-Physics(Hendrycks et al., 2021)를 사용하며, 이는 물리적 작업이지만 산술 기술에도 의존한다.

기본 기술은 도메인 간 데이터에서 효과적으로 일반화된다. 표 5에서 볼 수 있듯이, 적용 학습을 통해 모델은 원래 모델이 직접 답했던 방식과 달리 단계별 형식을 사용하여 응답을 생성한다. 이는 모델이 교차 데이터셋 분포에서 유래한 질문이라도 기술을 효과적으로 활용할 수 있음을 보여준다.
기본 기술은 도메인 간에도 일반화될 수 있으며 선택적인 적응력을 보인다. 표 5에서 모델은 원시 작업에서와 동일한 형식으로 물리적 양에 대해 산술을 수행하는데, 이는 기술 일반화가 교차 도메인 시나리오에서도 여전히 효과를 나타낸다는 것을 시사한다. LLM은 또한 보지 못한 데이터를 처리할 때 선택적인 적응력을 보인다. 예를 들어, 원시 작업에서 본 적이 없는 지수 값 “10−6”을 다룰 때, LLM은 이를 원래 형식으로 답하는 방식을 선택한다. 우리의 연구 결과는 기술 일반화를 유도하기 위해 적용 학습 중 일부 구성 데이터를 도입해야 하지만, 모든 작업에 대해 이를 제공할 필요는 없음을 보여준다. 그러나 다양한 시나리오에 적용할 수 있는 잘 설계된 원시 데이터는 필수적이다.
5.3 RQ3: 복잡한 작업이 기본 기술을 반대로 향상시킬 수 있는가? (RQ3: Can complex tasks help enhance atomic skills conversely?)
적용 학습 데이터 자체가 여러 기본 기술을 결합하고 있다는 점을 고려할 때, 구성 데이터가 기본 기술에 긍정적인 영향을 미칠 수 있음을 시사한다. 우리는 산술 기술을 평가하기 위해 테스트 데이터를 구성하고, 그 후 다른 훈련 전략을 적용한 모델을 평가한다.
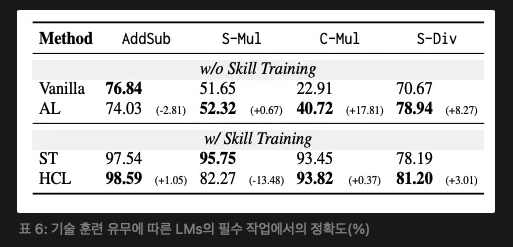
구성 데이터로 훈련하는 것이 기본 기술에 도움이 되지만 그 효과는 제한적이다. 표 6에서 볼 수 있듯이, 적용 학습은 SFT보다 모든 연산에서 더 나은 성능을 보이며, 이는 구성 작업이 원시 데이터에 반대로 긍정적인 영향을 미친다는 것을 보여준다. 이는 복잡한 추론 데이터셋에 대한 훈련이 특정 작업의 성능을 향상시킬 뿐만 아니라, 그에 대한 응답에서 구성 가능성이 있으면 원시 작업에도 이득을 준다는 유망한 결론을 이끈다. 우리는 이 개선에 대해 부록 D.2에서 추가로 논의한다. 또한, 구성 작업이 가져오는 이득은 미미하다. 적용 학습은 C-Mul에서 22.91%에서 40.72%로 향상시키는 데 그쳤고, 기술 훈련은 93.45%로 급격히 증가시켰다. 우리는 이를 적용 학습에 사용된 이질적인 데이터의 제한으로 설명한다. 원시 작업은 자동으로 많은 이질적인 데이터를 생성할 수 있지만, 구성 데이터는 복잡한 추론 작업에 대한 원래 훈련 세트의 제한에 의해 제한된다. 따라서 적용 학습만으로는 기본 기술을 충분히 향상시킬 수 없으며, 이는 계층적 커리큘럼 학습에서 기술 훈련 단계의 중요성을 더욱 강조한다.
구성 작업에 대한 지속적인 훈련은 기본 기술에 대한 급격한 망각을 초래하지 않는다. 기술 학습을 받은 모델은 이미 숙련된 기본 기술을 보유하고 있지만, 적용 학습에서 이질적인 데이터로 훈련하면 급격한 망각이 발생할 위험이 있다. 그러나 표 6에서 볼 수 있듯이, HCL은 대부분의 산술 연산에 대해 기술 훈련과 유사한 수준을 유지하는 것이 눈에 띈다. 이는 구성 작업에 대한 지속적인 훈련이 기본 기술의 재앙적 망각을 자발적으로 방지할 수 있음을 보여준다. 우리는 이는 S-Mul에서 구성 데이터의 연산이 제한적이어서 모델이 C-Mul 내의 다른 데이터에 의해 혼동될 수 있기 때문이라고 제안한다. 그러나 S-Mul 연산에서 이상 현상이 관찰되며, 이는 부록 D.3에서 추가로 논의한다.
Conclusion
이 연구에서 우리는 기본 작업에서 복잡한 추론 작업으로의 일반화에 대해 최초로 조사하였다. 우리는 수학 단어 문제를 연구 사례로, 산술과 단위 변환을 관련된 기본 기술로 선택한 탐색 프레임워크를 제안한다. 실험을 통해 기본 기술은 복잡한 추론 작업으로 자발적으로 일반화되지 않는다는 것을 밝혀냈다. 또한, 우리는 기술 일반화를 유도하는 계층적 커리큘럼 학습 전략을 제안하고 그 효과를 입증하였다. 우리의 실험 결과는 향후 복잡한 추론 작업을 위한 더 나은 훈련 전략을 설계하는 데 유용한 지침을 제공한다.
Limitations
이 연구에서는 수학 단어 문제를 연구 작업으로 선택했지만, 기본 기술에 의존하는 더 복잡한 추론 작업이 많이 존재한다. 예를 들어, 작업 계획, 시나리오 모델링, 의사 결정 등이 이에 해당한다. 비록 우리는 더 복잡하고 다양한 추론 작업에 대해 깊이 탐구하지 않았지만, 이 분야들은 향후 연구에서 특히 흥미로운 방향으로 떠오른다. 또 다른 제한 사항은 우리가 제안한 기술 일반화가 응답에서 명시적으로 나타낼 수 있는 기본 기술에 의존한다는 점이다. 암묵적인 기본 기술이 복잡한 추론 작업에 긍정적인 영향을 미칠 수 있는지는 확실하지 않다. 또한, 기본 기술의 정의와 원시 데이터 생성 방법은 수동으로 지정된다. 향후 연구에서는 계층적 커리큘럼 학습을 위한 완전한 프레임워크를 설계하기 위한 자동화된 방법론을 탐구할 가치가 있다.
Ethical Considerations
이 논문에서 사용된 모든 데이터 출처와 언어 모델은 공개되어 있다. 이 논문에서 대부분의 데이터 생성 및 평가는 자동화되어 있으며, § 5.1의 오류 분석을 제외한 모든 부분에서 인간 평가가 사용되었다. 인간 평가에 대한 세부 사항은 부록 C.2에 제공된다. 우리는 주석자의 개인정보 보호 권리를 보호한다. 모든 주석자는 지역 최저 임금 이상을 지급받았으며, 본 논문에 명시된 연구 목적을 위해 평가 데이터셋을 사용하는 것에 동의했다. 우리의 연구는 잠재적인 위험과 관련된 윤리적 고려 사항을 제기하지 않으며, 인간을 대상으로 한 연구를 포함하지 않는다.
부록
A. Detail for Training Data (훈련 데이터의 세부 사항)
A.1 Arithmetic Prerequisite Task (산술 원시 작업)

우리는 알고리즘 1에서 보듯이 규칙 기반 접근법을 사용하여 산술 원시 작업에 대한 데이터를 구성한다. 데이터의 난이도는 네 가지 측면을 고려한다: 홉의 수, 유효 숫자의 길이, 값의 유형, 연산의 유형이다. 홉의 수는 두 개에서 다섯 개까지 범위가 있으며, 홉이 많을수록 더 어려운 문제를 의미한다. 유효 숫자의 길이는 1에서 8까지 범위가 있으며, 숫자가 길어질수록 계산이 더 복잡하고 어려워진다. 값의 유형에는 모든 정수, 모든 실수, 혼합된 데이터 유형이 포함되며, 점차적으로 난이도가 증가한다. 연산 유형에는 덧셈과 뺄셈을 포함하는 AddSub, 단순 곱셈 연산(S-Mul), 복잡한 곱셈 연산(C-Mul), 그리고 단순 나눗셈(S-Div)이 포함된다. 이들 중 AddSub는 덧셈과 뺄셈만 포함하고, S-Mul은 유효 자리가 1인 두 번째 값으로 간단한 곱셈을 수행하며, C-Mul은 두 번째 숫자를 나누어 단계별로 계산을 수행하는 복잡한 곱셈을 포함하며, S-Div는 단순한 나눗셈을 나타낸다.
알고리즘 1에서 응답은 홉에 기반한 단계별 산술 과정을 보여준다. C-Mul 연산의 경우, 두 번째 값은 나누어지고, 그 후 비트 단위 곱셈과 결과 합산이 수행된다. SplitCOT, MulCOT, AddCOT는 각각 숫자 분할, 비트 단위 곱셈, 결과 합산 과정을 나타낸다.
A.2 Unit Conversion Prerequisite Task (단위 변환 원시 작업)
우리는 DimUnitKB(Huang et al., 2023)를 기반으로 단위 변환 원시 작업에 대한 데이터를 구성한다. 먼저, MWP에 포함된 단위의 양 타입을 추출하는데, 총 7가지 타입이 있다: 길이, 시간, 속도, 질량, 부피, 면적, 전력. 우리는 동일한 양 타입을 나타내는 단위에 대한 쌍별 변환 데이터를 구성하며, 이는 알고리즘 2에 상세히 나와 있다.

A.3 Compositional Data(복합 데이터)
응용 학습에서는 원자 기술을 복합 작업에 통합하는 데이터를 구성해야 한다. 복합 데이터 구성은 다음 단계를 포함한다:

- 복잡한 추론 작업의 훈련 세트에서 데이터 항목을 샘플링한다.
- 항목의 응답에서 원자 기술과 관련된 모든 구간을 추출한다.
- 알고리즘 1과 알고리즘 2의 ResponseGeneration 함수와 TextGeneration 함수를 사용하여 원자 기술에 대한 새로운 형식의 응답을 생성한다.
- 원자 기술과 관련된 모든 구간을 새로 생성된 답변 응답으로 교체하여 복합 데이터를 구성한다.
예를 들어, 산술에서 "12 37 = 448"이라는 산술 구간을 "리본의 총 길이는: 12 37 = 448 cm"라는 응답에서 추출한 후, 이를 "12 37 = 12 (30 + 7) = 12 30 + 12 7 = 360 + 84 = 444"로 교체하여 "리본의 총 길이는: 12 37 = 12 (30 + 7) = 12 30 + 12 7 = 360 + 84 = 444 cm"라는 복합 데이터를 얻는다.
B. Detail for Evaluation Data(평가 데이터의 세부 사항)
B.1 Deficiency of GSM8K in Skill Assessment(GSM8K의 기술 평가 부족)
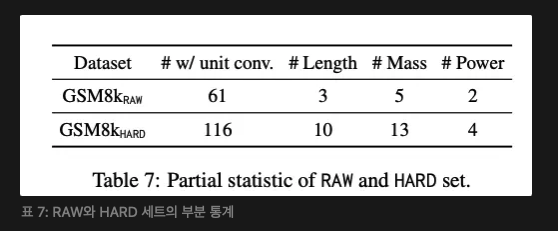
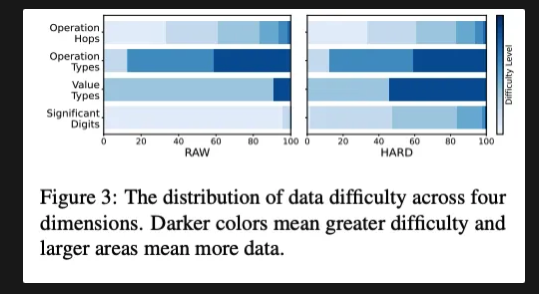
GSM8K(Cobbe et al., 2021)는 현재 수학 단어 문제에 널리 사용되는 평가 벤치마크이다. 그러나 이 데이터셋은 다양한 난이도 수준에서 기초 기술의 적용을 포괄적으로 다루지 않는다. 우리는 GSM8K가 산술 작업에서 난이도 범위를 어떻게 다루는지 분석하고, 섹션 A.1에서 언급한 네 가지 측면을 고려하여 Fig. 3 (왼쪽)과 같이 나타낸다. 더 어두운 색은 더 어려운 난이도를 의미하며, 더 큰 영역은 더 많은 데이터 양을 나타낸다. 이 결과는 GSM8K 테스트 세트가 다양한 연산 홉, 연산 유형, 값 유형을 포괄적으로 다루고 있음을 보여준다. 그러나 포함된 유효 숫자는 주로 간단한 데이터에 집중되어 있다. GSM8K 데이터셋은 또한 단위 변환 기술에 대한 포괄성이 부족하다. 이 통계는 Tab. 7에 나와 있다. 다양한 유형의 단위 표현을 일부만 다룬다.
B.2 Method for Data Augmenting (데이터 증강 방법)

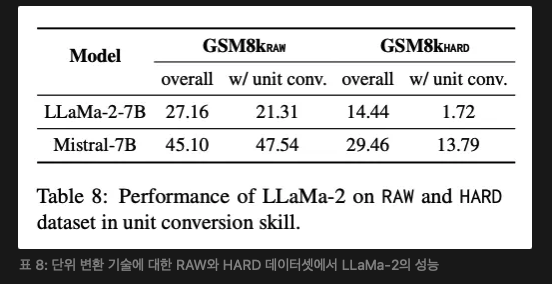
산술의 경우, 우리는 원래 문제의 논리를 변경하지 않고 유효 숫자 길이를 증가시켜 평가 데이터를 증강하며, 이를 HARD 세트로 명명한다. 알고리즘 3에 이 방법이 개략적으로 나와 있다. 먼저 질문에 있는 숫자와 답안에서의 중간 숫자, 그리고 이들 간의 계산 관계를 추출한다. 그런 다음, 최대 유효 숫자 길이를 기준으로 새로운 숫자를 무작위로 선택하고 이에 따라 새로운 중간 숫자를 계산한다. 이러한 업데이트된 숫자는 원래 질문과 답안에 통합되어 향상된 질문-답변 쌍을 생성한다. Fig. 3 (오른쪽)에서 보듯이, HARD 세트는 더 넓은 범위의 유효 숫자를 포함한다. 새로운 데이터 분포는 난이도가 증가함에 따라 적절하게 비율이 감소하는 합리적인 분포를 보인다. 단위 변환의 경우, 우리는 다양한 단위 표현을 포함하여 테스트 데이터를 증강한다. 이 방법은 알고리즘 3에 개략적으로 나와 있다. 우리는 RAW와 HARD에서 LLaMA-2를 평가한다. Table 8에서 보듯이, 결과는 HARD 세트가 더 큰 차별화를 제공한다는 것을 나타낸다.
C Experimental Details(실험 세부 사항)
본 논문에서 다룬 모든 언어 모델(LM)의 구현은 HuggingFace Transformers2와 Deepspeed3를 기반으로 한다. 학습률은 1e-5, 1e-6으로 설정하고, WarmupLR 스케줄러를 사용하며, 배치 크기는 32, 최대 시퀀스 길이는 1024로 설정하고 8 에폭 동안 학습을 진행한다. 모든 실험은 NVIDIA A800 PCIe 80GB 메모리를 탑재한 워크스테이션에서, Ubuntu 20.04.6 LTS와 torch 2.0.1 환경에서 수행된다. 평가에서는 vllm 4를 사용하여 추론을 진행한다. 모든 결과는 탐욕적 디코딩 전략(greedy decoding strategy)을 사용하여 생성된다.
우리는 선행 데이터에 대해 추가적인 프롬프트를 사용하지 않으며, MWP의 학습과 테스트에는 Alpaca (Taori et al., 2023)의 프롬프트를 사용한다.
C.1 The Ratio Selection for Replay Strategy(리플레이 전략을 위한 비율 선택)

우리는 일부 학습 예제를 MWP에서 보존하고 이를 선행 작업 데이터와 혼합하여 모델이 기술 학습에서 원래의 문제 해결 능력을 유지하도록 한다. 그림 7은 선행 작업(기초 기술)과 복잡한 추론 작업에서 다양한 혼합 비율에 따른 모델의 성능을 보여준다. 전반적으로 선행 데이터의 비율이 증가함에 따라 모델은 원자 기술에서 더 나은 성능을 보이고 MWP 해결에는 더 나쁜 성능을 보인다. 균형 잡힌 혼합 비율은 기술에 따라 다르다. 산술 연산은 단위 변환보다 더 많은 선행 데이터가 필요하다. 결국 우리는 산술 연산을 위한 혼합 비율을 10, 단위 변환을 위한 비율을 1로 설정하여 상대적으로 효과적인 지속 학습을 달성했다.
C.2 오류 분석을 위한 인간 평가
우리는 수학 단어 문제에 대해 오류 분석을 수행할 인간 평가자를 모집했다. 모든 평가자는 수학에 대한 충분한 지식을 갖추고 있으며 평가 기준에 필요한 배경 정보를 제공받았다. 각 항목은 최소한 세 명의 평가자가 주석을 달며, 불일치가 발생하면 재평가가 이루어진다.
응답의 평가는 네 가지 유형으로 나뉜다:
- 기술 오류: 기본 기술 세그먼트 내에서 발생하는 오류, 예를 들어 복잡한 곱셈 수행에서의 오류
- 질문 오해: 질문을 잘못 이해하여 잘못된 값을 사용하는 경우
- 추론 오류: 추론 과정에서 오류로 인해 잘못된 표현이 발생하는 경우
- 정확함: 추론 과정과 답이 모두 완전히 정확함을 나타냄이 네 가지 분류의 우선순위는 순서대로 감소한다.
D. Additional Results (추가 결과)
D.1 The correlation of atomic skills(기본 기술 과의 상관관계)
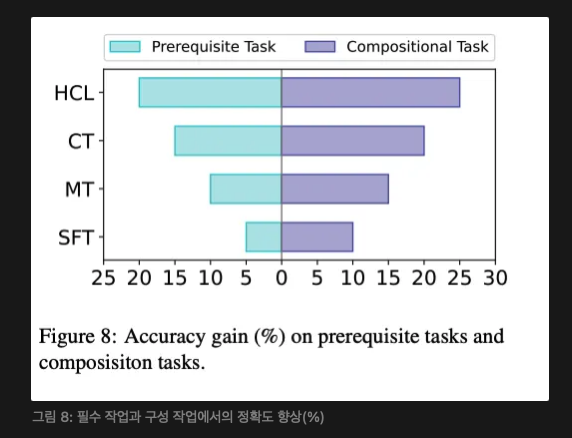
그림 8은 선행 작업과 조합 작업에서의 정확도 향상 간의 상관관계를 보여준다. 선행 작업에서 더 높은 성과를 보인 모델은 더 강한 원자 기술을 가짐을 의미하며, 이는 모델의 기본 기술과 조합 작업을 해결하는 능력 간에 긍정적인 상관관계가 있음을 나타낸다. 이는 우리의 방법에 의해 얻어진 향상이 기본 기술의 향상 덕분임을 뒷받침하는 결과이다.
D.2 Compositional task is not enough to enhanced atomic skills (조합 작업만으로는 기본 기술을 충분히 향상시킬 수 없다)
우리는 섹션 5.3에서 조합 작업이 기초 기술을 향상시킨다고 언급했지만, 그 효과는 제한적이라고 설명했다. 표 9에서 볼 수 있듯이, AL 방법은 COT 형식으로 답변을 학습했지만, 완전한 지식을 습득하지 못했기 때문에 완전한 정답을 도출할 수 없다.
D.3 Abnormal Results in S-Mul(S-Mul에서의 비정상적인 결과)
우리는 섹션 5.3에서 HCL이 S-Mul에 대해 ST에 비해 비정상적인 감소를 보인다고 언급했다. 대부분의 오류는 크기 단위에서 잘못된 결과가 나오는 경우에서 발생한다. 예를 들어, HCL 모델은 "2.61 * 0.01"을 계산할 때 "0.00261"이라고 응답했으며, 올바른 답은 "0.0261"이다. 이는 주로 특별한 연산인 S-Mul이 조합 데이터에서 거의 발생하지 않기 때문이라고 주장한다. 우리는 모든 값을 균일하게 샘플링하기 때문이다. 반면 기술 학습 단계에서는 S-Mul 연산을 위한 대량의 학습 데이터를 구성했다. 이는 섹션 5.3에서 언급한 "급격한 망각 방지" 특성이 조건적임을 나타낸다. 조합 데이터 내에서 원자 기술의 분포가 선행 작업과 일치해야 한다. 그렇지 않으면 급격한 망각 현상이 발생할 수 있다.
D.4 Additional Examples on MWP(MWP에 대한 추가 예시
우리는 섹션 5.1을 보완하기 위해 더 완전한 예시를 추가했다. 이 예시는 표 10에 제시되어 있다.
참고: 계층적 커리큘럼 (Hierarchical Curriculum)
교육학에서의 계층적 커리큘럼은 학습 내용을 단계적으로 조직하여 학생들이 점진적으로 더 높은 수준의 지식과 기술을 습득할 수 있도록 설계된 교육 과정을 의미. 학습 내용이나 과제가 상호 연계되어, 기초적인 내용을 충분히 이해한 후에 더 복잡하고 심화된 내용으로 나아가도록 구성됨.예시: 수학 교육의 계층적 커리큘럼
- 기초 연산 (기본 수학)
- 학습 목표: 덧셈, 뺄셈, 곱셈, 나눗셈의 기본 개념을 이해하고 수행할 수 있다.
- 활동: 숫자 카드를 사용하여 덧셈과 뺄셈 연습, 나누기와 곱셈의 표를 암기.
- 정수 및 분수 (중급 수학)
- 학습 목표: 정수, 분수, 소수의 개념을 이해하고 기본 연산을 할 수 있다.
- 활동: 분수를 더하고 빼는 연습, 소수를 정수로 바꾸는 연습, 분수와 소수의 비교.
- 대수 (고급 수학)
- 학습 목표: 대수적 표현을 이해하고 식을 풀 수 있다.
- 활동: 간단한 일차방정식 풀기, 변수와 상수의 개념 이해, 대수적 규칙 적용.
- 기하학 (고급 수학)
- 학습 목표: 평면 기하학의 기초적인 개념을 이해하고 도형의 성질을 파악할 수 있다.
- 활동: 삼각형, 사각형, 원의 성질을 배우고, 면적과 둘레를 구하는 문제 해결.
- 미적분 (심화 수학)
- 학습 목표: 함수와 그래프의 관계를 이해하고, 미분과 적분의 기초 개념을 익힐 수 있다.
- 활동: 함수의 그래프 그리기, 기울기 계산, 적분을 통한 면적 구하기.
- 통계 및 확률 (심화 수학)
- 학습 목표: 데이터 분석 및 확률 이론을 이해하고 활용할 수 있다.
- 활동: 평균, 중앙값, 표준편차 계산, 확률 문제 해결.
각 단계의 설명
- 1단계에서는 기본적인 수학 개념을 익히고, 이를 바탕으로 점차 더 복잡한 수학 개념을 학습해 나갑니다.
- 2단계에서는 분수나 소수와 같은 조금 더 고급 수학 개념을 다루며, 기초 연산을 응용합니다.
- 3단계에서는 대수적 사고를 통해 문제 해결 능력을 키우고, 4단계에서는 도형에 대한 이해를 통해 기하학적 사고를 배웁니다.
- 5단계에서는 미적분학의 기초를 배우고, 6단계에서는 통계와 확률을 통해 실생활 문제에 적용할 수 있는 수학적 접근을 학습합니다.
이와 같이 계층적 커리큘럼은 각 단계를 체계적으로 구성하여, 학생이 자연스럽.게 더 어려운 개념을 이해하고 적용할 수 있도록 도움.
