네트워크 연결 : https://www.acmicpc.net/problem/1922
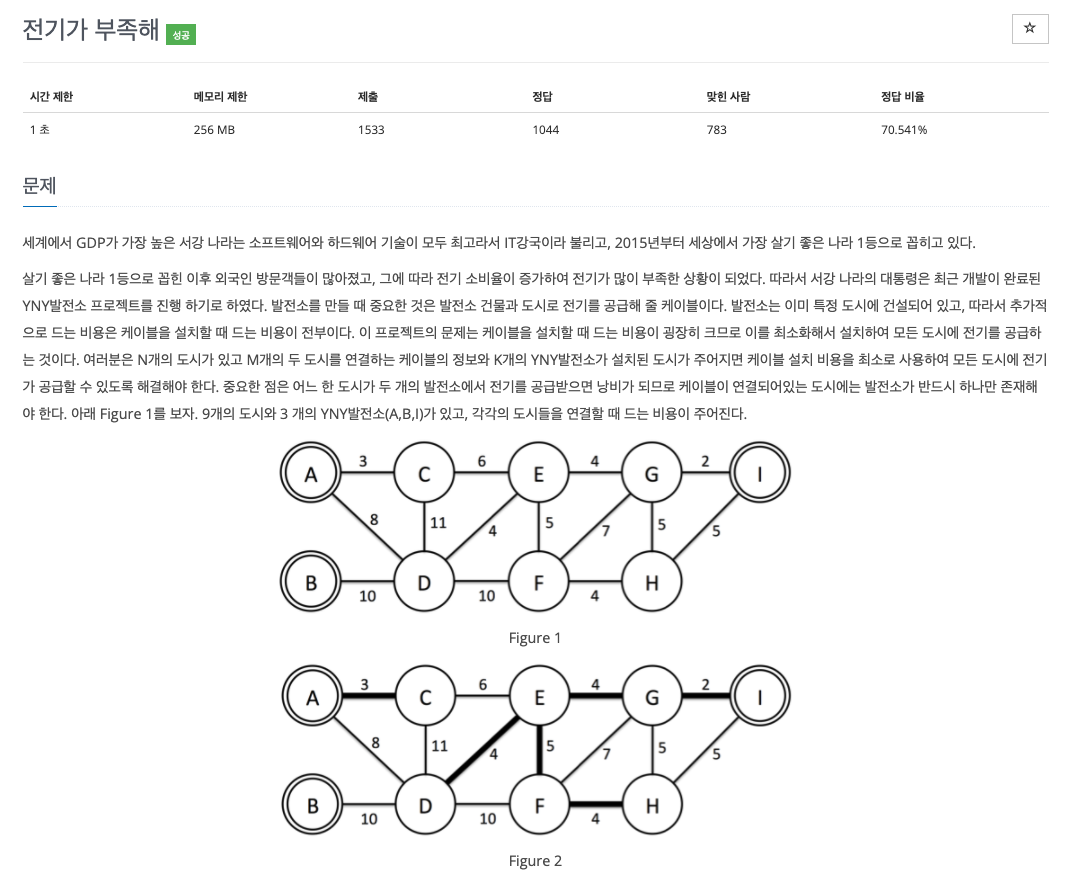

해당 문제를 풀기 전 '최소신장트리(Minimum spanning tree)'를 알아야 한다.
노드를 전체 돌 되, 가장 적은 비용으로 돌 수 있는 방법을 구하는 문제이며 통신네트워크 구축과 같은 문제로 많이 출제된다.
또한 최소 신장 트리는 사이클을 포함하지 않고, 최소비용의 간선으로 구성되어 있다.
크루스칼 알고리즘(Kruskal Algorithm)
나는 크루스칼 알고리즘을 이용했는데, greedy 알고리즘을 이용하여 네트워크의 모든 정점을 최소 비용으로 연결하는 해답을 구하는 방법이다.
해결 로직은 다음과 같다.
1. 그래프의 간선들을 오름차순으로 정렬한다.
2. 사이클을 만들지 않는 간선을 선택한다.
3. 해당 간선을 최소 비용 신장 트리의 집합에 추가한다.
예를 들어서 설명해보자.
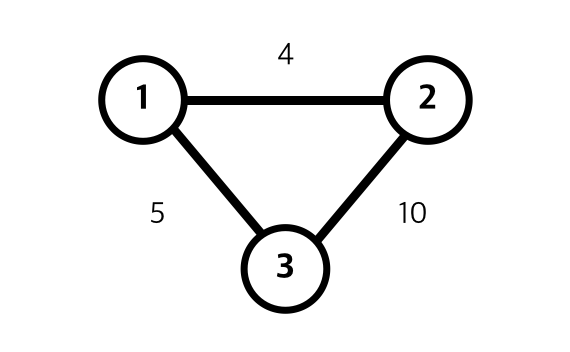
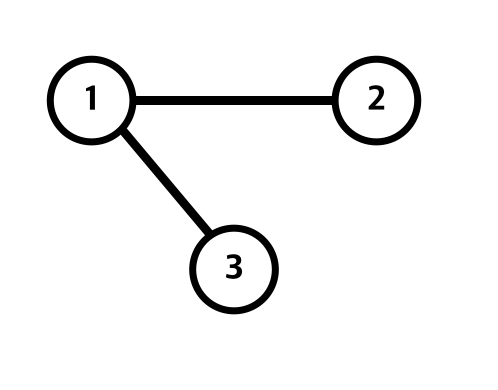
1과 3을 이어주는 간선은 5라는 비용이 든다.
2와 3을 이어주는 간선은 10이라는 비용이 든다.
1과 2를 이어주는 간선은 4라는 비용이 든다.
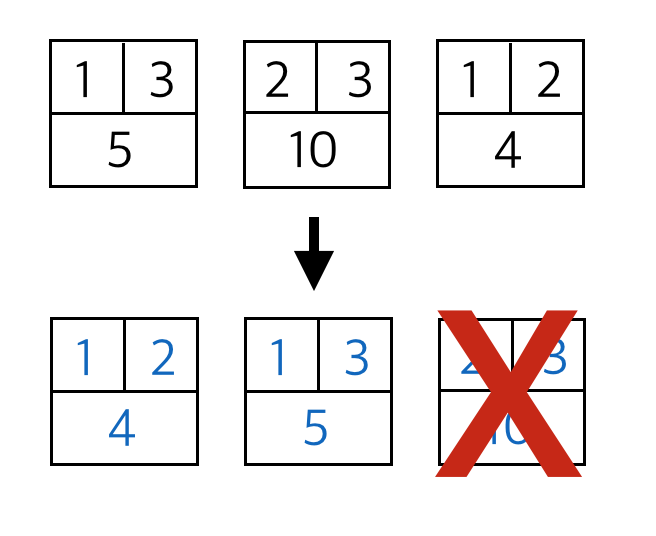
그러면 이 간선들을 이렇게 풀어주고 정렬해준다.
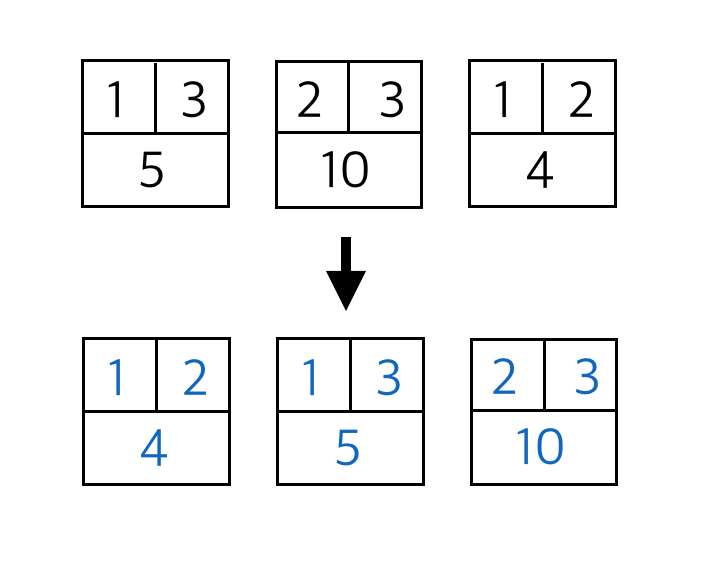
그러면 이제 사이클을 만들지 않는 간선을 선택해준다.
가장 최소값인 1과 2를 연결해주고,
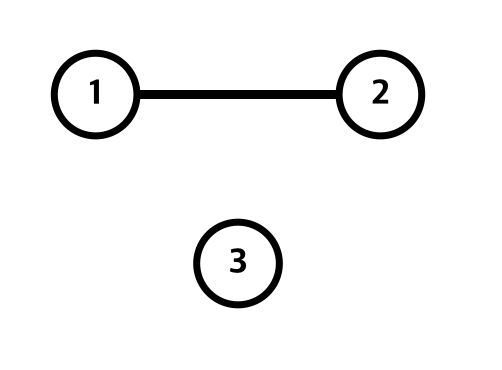
그 다음으로 작은 값인 1과 3을 연결해준다.
맨 마지막 노드가 남았지만, 이 노드를 연결하는 순간 사이클을 돌게 되므로 연결하지 않는다.
그렇다면, 사이클이 생기는지 어떻게 체크할 수 있을까?
여기서 Union-find 개념이 등장하는데,
각 노드의 조상(부모)노드를 찾고(find) 조상 노드가 다르면 연결시켜준다(union).
그리고 나서 연결(union)시켜줄 때 마다 비용을 계산해주면 끝!
from gettext import find
import sys
from collections import deque
from unittest import result
input = sys.stdin.readline
# 컴퓨터의 수
N = int(input())
# 선의 수
M = int(input())
parent = [i for i in range(N+1)]
edges = []
for _ in range(M):
a, b, cost = map(int, input().split())
edges.append((cost, a, b))
# 최소길이로 정렬해 놓음
edges.sort()
# 부모 노드를 찾아야함 -> 사이클을 만들지 않기 위해서
# 부모 노드를 찾기 위해서는 union-find를 사용한다.
# 재귀함수를 통해 가장 작은 값을 가리키는 것을 찾아줌
# ex) 1-2-3이 연결되어 있으면 table은 1 1 2 가 될 것임, 3은 2와 연결되어있고 재귀함수를 통해 2의 연결 값인 1을 연결해준다.
def get_parent(parent, x):
if parent[x] == x:
return x
parent[x] = get_parent(parent, parent[x])
return parent[x]
# 사이클이 없으면 합쳐준다
def union(parent, a, b):
a = get_parent(parent, a)
b = get_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
def kruskal(edges):
result = 0
for edge in edges:
cost, a, b = edge
if get_parent(parent, a) != get_parent(parent, b):
union(parent, a, b)
result += cost
return result
result = kruskal(edges)
print(result)이 문제와 1197 문제는 입력받는 부분만 다르고 똑같다.
다음 포스팅은 현재 개념에서 조금 더 심화된 문제인 '전기가 필요해(https://www.acmicpc.net/problem/10423)' 를 풀 예정이다.
