
이번 문제는 구간트리(Segment Tree)를 이용하는 문제 중 가장 기초문제이다. 하지만 문제 자체가 매우 쉬워서 구간트리는 사용하지 않아도 된다.
구간트리란 특정 구간에서 특정한 값을 탐색하는 효율적인 알고리즘이다.
예를 들어서 설명해보자면 배열 [5,4,3,2,1]의 구간합들을 먼저 구해놓아서 실제 계산하는 시간을 줄이는 알고리즘이라고 생각하면 된다.
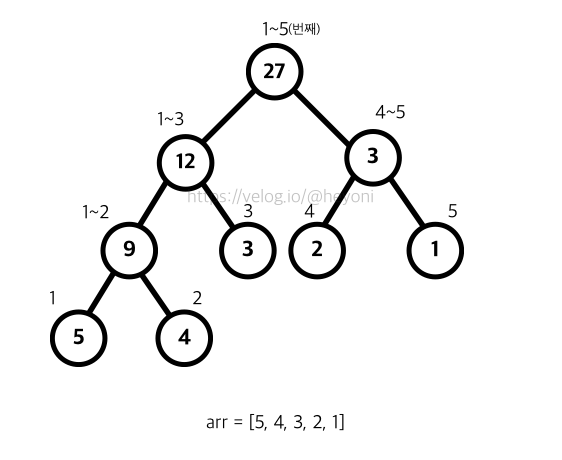
사진에서 노드 위에 붙어있는 숫자는 우리가 일반적으로 사용하는 순서(1번째, 2번째...)이다. 개발자들이 사용하는 0부터 시작하는 순서가 아님!
위와 같이 트리로 만들고
segmentArr에는 [0, 27, 12, 3, 9, 3, 2, 1, 5, 4]와 같이 저장해준다.
오늘 풀 문제는 segment 트리를 이용하지 않고 다른 방법을 이용하여 풀 예정인데, 위에서 얘기했던 segment Tree와 방법이 아예 달라서 그냥 개념만 알아두면 된다.
풀이 과정은 다음과 같다.
1. '누적합'을 구한다.
2. 구할 범위에서 누적되지 않은 범위를 빼준다.
끝이다.
매우 간단함!
예를 들어서 배열 [5, 4, 3, 2, 1]이 주어졌고
여기서 누적합을 구하면 [5, 9, 12, 14, 15]이다.
2~3번의(배열 인덱스 아니고 순서임) 누적합을 구하고 싶다면 누적합 3번에서 누적합 1번을 빼주면 된다.
[5, 5+4, 5+4+3, 5+4+3+2, 5+4+3+2+1] 으로 생각하면 더 쉬울 것 같음!
즉, sum_list[j] - sum_list[i-1]의 값이 답이라고 할 수 있겠다.
코드는 다음과 같다.
import sys
input = sys.stdin.readline
N, M = map(int, input().split())
arr = list(map(int, input().split()))
sum_list = [0]
total = 0
for i in range(len(arr)):
total += arr[i]
sum_list.append(total)
for _ in range(M):
i, j = map(int, input().split())
print(sum_list[j] - sum_list[i - 1])